2014年天津卷理科压轴题命题手法探究*
2020-05-03杨苍洲
高中数学教与学 2020年3期
杨苍洲
(福建省泉州第五中学,362000)
一、缘起
笔者在朋友圈发布了一篇关于“定比分点与压轴题命制”的小文,恩师许银伙老师竟认真看完全文,并对试题解法提出了自己的看法.对此,我与他交流了此类函数零点问题的解题方法.其间,许老师谈及2014年高考天津卷理科的压轴试题,谈及试题的解法及对学生的讲法,实在难以解释参考答案中的神来之笔.受其启发,我打算从试题的命题角度揭示试题的解法,从而理顺解题思路.
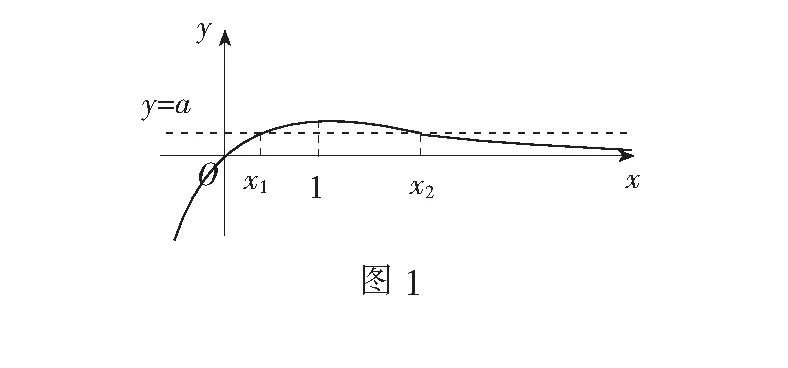
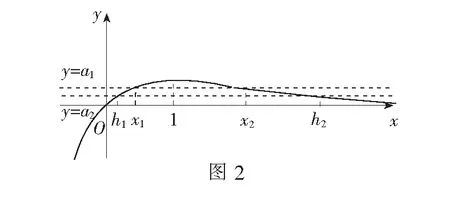
试题呈现 设函数f(x)=x-aex(a∈R),x∈R,已知函数y=f(x)有两个零点x1、x2,且x1 (1)求a的取值范围; (3)证明:x1+x2随着a的减小而增大. 我们知道,“函数零点”问题可以转化为“方程的根”问题,也可以转化为“两条曲线的交点”问题.既然如此,我们转化一下视角,来研究曲线g(x)与动直线y=a的交点问题. 问题1 已知函数f(x)=x-aex有且只有两个不等实根,求a的取值范围. 继续观察图象,设这两个实根为x1、x2,且x1 ①x1<1 ③ 随着a的增大,x2变小的速度较快,x1增大的速度较慢,因此x1+x2在减小. 于是可设置如下问题2. 综合上述问题1、2,即可得2014年高考天津卷理科的压轴试题. 试题(1)的求解较为简单,此处不再赘述. ① 因此,由①式可得x1+x2随着t的增大而增大.而由(2),t随着a的减小而增大,所以x1+x2随着a的减小而增大. 采用这种命题手法,笔者命制如下两个新题,共读者赏析. 题1 已知函数f(x)=lnx-ax有两个零点x1、x2,且x1 (1)求实数a的取值范围; 题2 已知函数f(x)=x2ex-ax有三个零点. (1)求实数a的取值范围;二、命题手法探究
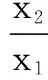
三、解题手法探究
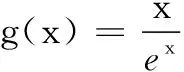
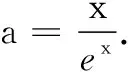
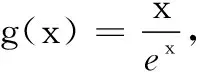
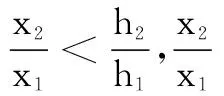
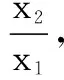
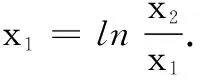
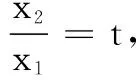
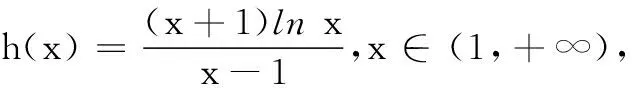
四、新题命制