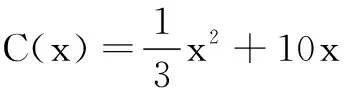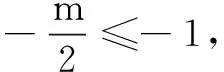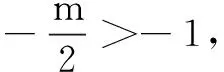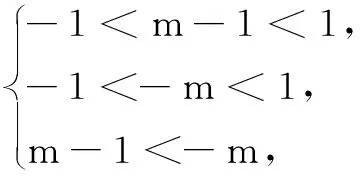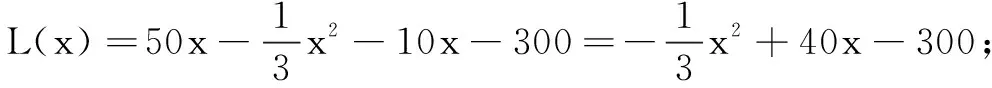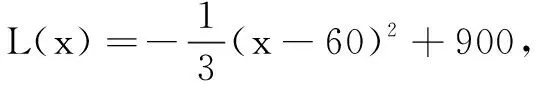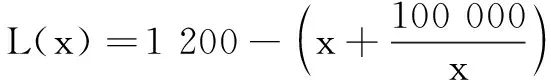高一数学测试

一、填空题(本大题共有12小题,每小题4分,共计48分)

1.已知集合A={x|x∈Z，-1≤x≤1},集合B={0,1,2},则A∩B=( )

(A)[0,1] (B){0,1}

(C)[-1,2] (D){-1,0,1,2}

2.2020°角的终边在( )

(A)第一象限 (B)第二象限

(C)第三象限 (D)第四象限

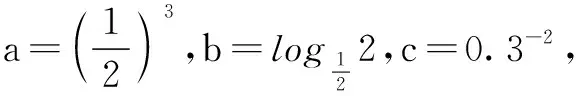
(A)a>b>c(B)a>c>b

(C)c>a>b(D)b>a>c

(A)(0,2] (B)(1,2]

(C)(0,1)∪(1,2) (D)(0,1)∪(1,2]

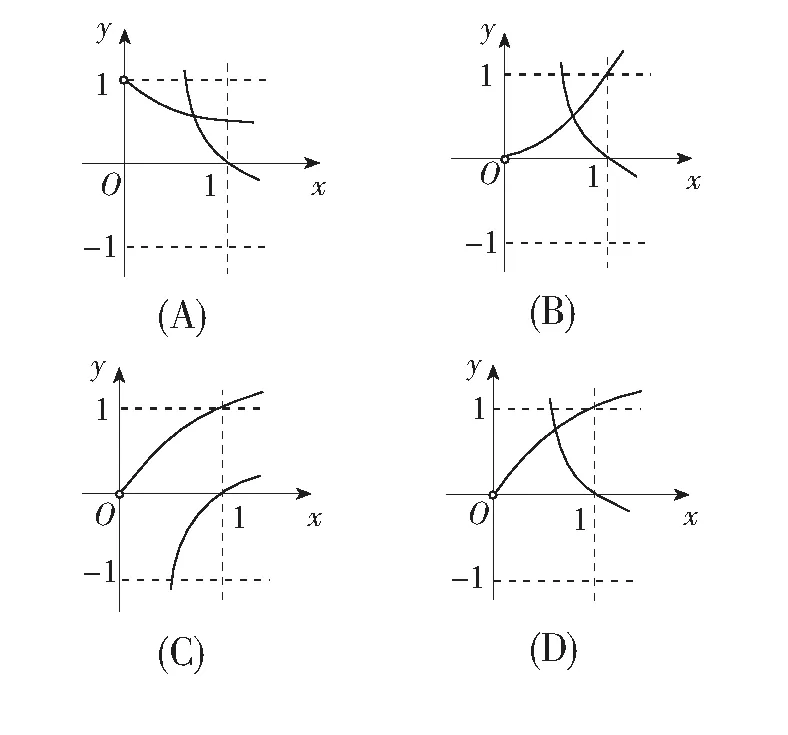
5.已知a>0且a≠1,则在同一直角坐标系中函数f(x)=xa(x>0),g(x)=logax的图象可能是( )

6.下列函数中,既是偶函数又在(0,+∞)内单调递增的函数是( )

(A)y=1-x2(B)y=x3

(C)y=lnx(D)y=|x|+1

7.函数f(x)=2-xlnx的零点所在的区间为( )

(A)(0,1) (B)(1,2)

(C)(2,3) (D)(3,4)

8.已知函数y=a2x+b+m(a>0且a≠1)恒过定点(2,2),则b+m=( )

(A)-3 (B)3 (C)-4 (D) 4

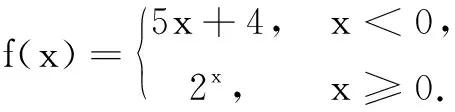
(A)0 (B)1 (C)2 (D)4

10.已知函数f(x)是定义在R上的奇函数.且当x≤0时,f(x)=3x+a,则f(log94)的值为( )

11.设a>0且a≠1,函数f(x)=loga|ax2-x|在[3,4]上是增函数,则a的取值范围是( )

12.已知定义在区间[0,2]上的函数f(x)=ln(2ex+3x-a),若存在m∈[0,1],使f(f(m))=m成立,则a的取值范围为( )

(C)[1,e+2] (D)[1,e+3]

二、填空题(本大题共4小题,每小题5分,计20分)

13.已知扇形的圆心角为150°,弧长为5π(rad),则扇形的半径为______.

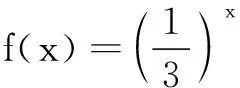
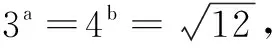
16.已知函数f(x)=x-ln(1+x2),若f(m)-f(1-m)≥2m-1,则实数m的取值范围为______.

三、解答题(本大题共6小题,第17题10分,其余各题12分,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)

18.已知全集U=R,集合A={x|-3≤x≤1},B={x|(x+3)(x-a)<0},且a>0.

(1)若a=3,求A∪B;

(2)若B⊆A,求实数a的取值范围.

19.已知幂函数f(x)=(p2-4p+4)x-p2+2p满足f(1)

(1)求函数f(x)的解析式；

(2)设函数g(x)=f2(x)+mf(x)+p,x∈[-1,+∞),是否存在实数m使得g(x)的最小值为-3?若存在,求出m的值;若不存在,说明理由.

(1)用定义证明函数y=f(x)是(-1,1)上的增函数;

(2)求关于m的不等式f(m-1)+f(m)<0的解集.

(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;

(1)若函数f(x)的定义域为R,求实数a的取值范围;

(2)当a=1时,若函数g(x)的图象上存在A、B两个不同的点与h(x)图象上的A′、B′两点关于y轴对称,求实数b的取值范围.

参考答案

一、选择题

1.B； 2.C; 3.C; 4.D; 5.D; 6.D;

7.C; 8.A; 9.B; 10.C; 11.D; 12.B.

二、填空题

三、解答题

18.(1)若a=3,则B={x|(x+3)(x-3)<0}={x|-3

∴A∪B={x|-3≤x<3}.

(2)∵a>0,∴B={x|-3

∵B⊆A,即{x|-3

19.(1)∵f(x)为幂函数,∴p2-4p+4=1,得p=1或p=3.

当p=1时,f(x)=x在(0,+∞)单调增,满足f(1)

当p=3时,f(x)=x-3在(0，+∞)单调减,f(1)>f(2),不符合题意.

综上，f(x)=x.

(2)由(1)可知g(x)=x2+mx+1,x∈[-1,+∞).

综上，m=-4或m=5.

由-10,x21+1>0,x22+1>0,有f(x1)-f(x2)<0,即f(x1)

由f(m-1)+f(m)<0，得f(m-1)<-f(m)=f(-m), 又f(x)在(-1,1)单调增,故

21.(1)x千件商品销售额为50x万元.

因为900<1 000,所以当产量为100千件时,该厂在这一商品中所获利润最大.

答:年产量为100千件时,该厂在这一商品中所获利润最大.

22.(1)由题意，知ax2-x+1>0对x∈R恒成立.

当a=0时,-x+1>0,不符合题意,舍去.