恒成立问题的三种常用解法

郭 维

(甘肃省张掖中学，734000)

在恒成立问题背景下求参数的取值范围是一种常见题型.本文以一道高三数学模拟试题为例，引出三种常见解法,彰显三种思想在解题中的应用，帮助同学们熟悉和熟练掌握此类问题的解法.

(1) 当a=1时,讨论f(x)的单调性;

(2) 若f(x)≥-1在[1,+∞)上恒成立,求实数a的取值范围.

解 (1)略.

(2)解法1 类比法

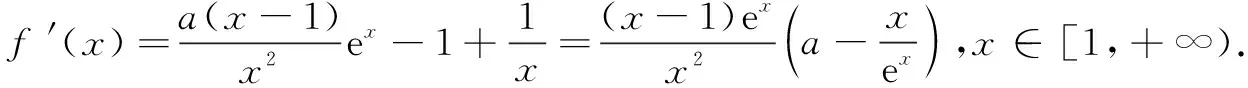
当a≤0时,f′(x)≤0,f(x)在[1,+∞)单调减,且f(1)<-1,不合题意.

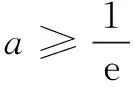
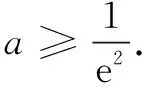
评注 类比第(1)问,延续第(1)问的做法循规滔距,顺应自然,这往往是最直接,最容易想到的一种做法.

解法2 分离参数法

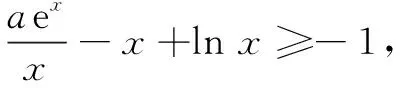
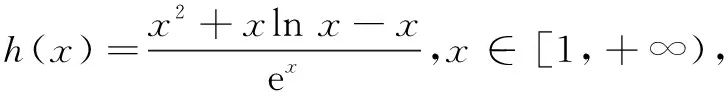
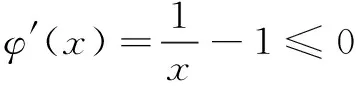
而φ(1)=1>0,φ(4)=ln 4-2<0,存在x0∈(1,+∞),使得φ(x0)=lnx0-x0+2=0,即lnx0=x0-2，则f(x)在(1,x0)单调增，在(x0,+∞)单调减.故

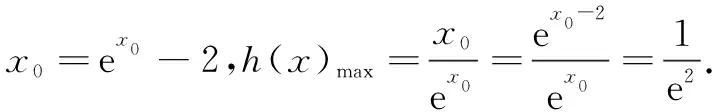
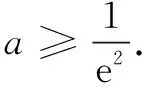
评注 分离参数思路清晰、有章可循、操作性强、易于掌握.

解法3 换元转换法

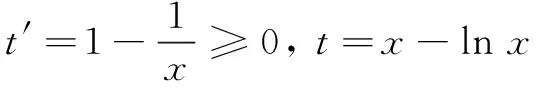
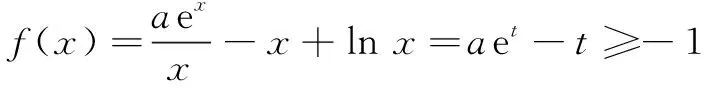
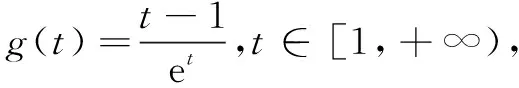
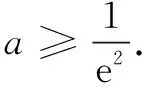
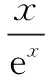
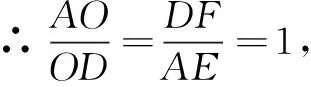
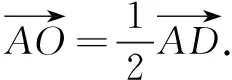
思路2 向量法