消“元” 消“差” 转换——处理一类多元变量最值问题的关键词

丁 强

(江苏省无锡市太湖高级中学,214125)

多元变量的最值及衍生问题在近年的高考、模考中频频出现,因其难度大、技巧强、灵活多变而具有挑战性,构成学生的难点.同时,这类最值问题中蕴含着丰富的数学思想和方法,有利于培养学生联想、转换的能力.因此,怎样求多元变量的最值,既是师生们非常关注和必须解决的问题,也是高考学子必备的解题技能.请看近几年江苏高考数学卷的几道填空压轴试题.

试题2 (2016年卷)在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是______.

试题3 (2018年卷) 在∆ABC中,角A、B、C所对的边分别为a、b、c,∠ABC=120°,∠ABC的平分线交AC与点D,且BD=1,则4a+c的最小值为______.

从上述简单的列举不难发现,江苏高考数学卷填空压轴题比较青睐于最值问题.其特点之一是涉及到多元(二元、三元)函数的最值；特点之二是侧重于一类三角形中三角函数的最值.有的问题一时找不到解答思路,有的问题运算量大、解答繁琐,令许多考生望而生畏.以下通过一组高考及模考试题的分析与求解,获得多元变量最值问题的处理策略,抽象成一组关键词,与大家分享.

一、消“元”

对于多元最值问题的解答思路,既然是多“元”,其基本思路自然是消“元” (或称减“元”),转换为熟悉的一元问题求解,或是转化为二元变量,用不等式的均值定理求解.

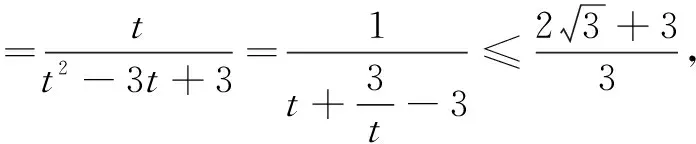
分析 关注目标,欲求一个含三元变量的一次分式型的最小值,考虑消元法.

故M的最小值为8.

评注 例1和2都是从目标出发,结合条件,采取合理的手段消元,使变量减少,便于找到解题途径 消元后为了简便运算,又进行了换元,使数量关系单一化.

二、 消“差”

这里的消“差”,指的是消除差异.解题差异论认为,解题的过程就是消除条件与条件,条件与结论之间差异的过程.[1]这需要我们注意观察,依据问题的形式特点和结构特征,要消除条件与目标之间的差异.对三角问题，利用消除整体与局部的差异,消除不同(函数)名、不同角、不同次数的差异，是解决一些问题的利器.

解 由a2-2ab+b2=4(ab)3,两边同加上4ab,得a2+2ab+b2=4(ab)3+4ab,即(a+b)2=4(ab)3+4ab.联想目标,两边同除以(ab)2,得

例4 见上述试题2.

分析 这是一个三元最值问题，由内角和定理A+B+C=π,自然想到消元；消哪一个?由条件sinA=2sinBsinC,考虑形式的对称性,选择消sinA,由A=π-(B+C)，将条件等式转化为二次齐次式.

再考虑到条件是正弦函数,目标是正切函数,要消除函数名称差异,选择弦化切.

解 由sinA=sin(B+C)=sinBcosC+cosBsinC=2sinBsinC,两边同时除以cosBcosC,得

tanB+tanC=2tanBtanC.

①

tanAtanBtanC

设tanBtanC=x(消元,也可视为整体消元,二元变一元),结合∆ABC是锐角三角形,再利用基本不等式,可求得tanAtanBtanC的最小值是8.

评注 例3、4解题的关键是在关注条件与目标的差异过程中采用对称消元、整体消元的方法逐步消除差异(包括结构差异,名称差异,次数差异等).

三、转换

转换即变换考察问题的角度.在分析、解决问题的过程中,当用某种思路解答遇到困难时,不妨换个角度进行考察,可能会柳暗花明.常见的思路有数与形的转换、正反转换、动静转换,一般问题(代数、几何、三角)转换为解析问题,一般与特殊的转换等,这些不仅有益于拓展解题思路,还有益于克服思维定势,培养学生思维的灵活性与敏捷性.

例5 设∆ABC的面积为2,若角A、B、C所对的边分别为a、b、c,则a2+2b2+3c2的最小值为______.

解 以AB所在直线为x轴,中垂线为y轴,建立直角坐标系,则

评注 本题是一道解三角形问题,用常规的正弦、余弦定理等知识求解,显得困难重重.我们可转换一个视角——解析法,建立合理的坐标系,把三个变量其中之一的c作为常数,其它变量a、b用c及x表示,再用二次函数和基本不等式知识，使问题轻松获解.

解 联想到目标式、条件式背后的几何意义，问题等价于曲线y=x2-2lnx与直线y=3x-4上两个动点P(a,b)、Q(c,d)的距离的最小值的平方.这就将问题转化为一个常规的问题,是数与形的转换.

评注 这些试题的解法给我们以启示:其一,换一个思路可能有惊喜!“数”、“形”需要经常转换与结合;其二,例5的解法可以推广,只要给出一个面积或周长的条件,求含系数平方和的形式,都可用解析法求解.

(1)试确定A、B的位置，使∆OAB的周长最大；

(2)当∆OAB的周长最大时，设∠DOC=2θ，试将运动休闲区ABCD的面积S表示为θ的函数，并求出S的最大值.

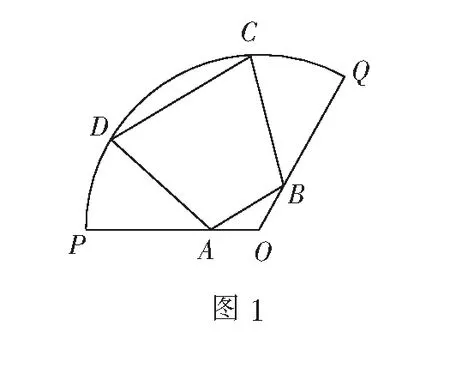
解 (1)略.

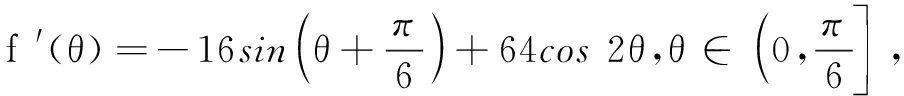
评注 一道整体求解繁琐的问题，转换思维角度，局面处理，利用函数的单调性成功突破，从中彰显了思维转换的魅力.它启示我们，要克服学生的思维定势问题，需要经常转换思维角度，从不同角度解决问题.

经过多年的教学探索,我们觉得解决一类多元变量最值问题的关键词是:消“元” 、消“差”、转换等.它们之间是一个整体,在目标意识统领下,三个关键词是相互联系的,有时可独立使用,有时需要结合使用,需因题而异.通过消“元”、消“差”及转换，可以拓展解题思路、快速寻求解题突破口,帮助学生释疑解惑,解答的成功感让学生倍感轻松与愉悦,从而增强数学学习的信心.