概率中的六个易混淆问题分析

王生林

(甘肃省高台县第一中学，734300)

概率是高中教材的新增内容,它是以实际应用问题为载体,以排列组合和概率的相关知识为工具,以考查对五个概率事件的判断识别及其概率的计算和应用为目的的一类必考题型.但由于其概念具有一定的抽象性和相似形,有些问题看似相同,实则不同,在解题时稍有疏忽就会致错．本文就以概率学习中几个易混淆的问题予以剖析,以期对同学们的学习有所帮助．

一、 等可能事件中的“等可能”与“非等可能”混淆

例1 投一枚骰子两次,求两次点数之和是3的概率．

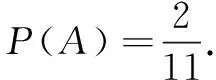
分析 错解将投一枚骰子两次出现的点数之和的所有可能取值归结为2,3,4…,11,12时,其中每一个结果的出现不是等可能的(如和为2只有(1,1)一种情况,而和为3的情况有(1,2)与(2,1)两种,其它的情况可类推),既然每一个结果的出现不是等可能的,就不可套用等可能事件中的概率计算公式进行计算．

正解 记所求事件为A,因为投一枚骰子两次出现的所有可能的情况是:(1,1)，(1,2)，…,(1,6),(2,1)，(2,2),…,(2,6),…,(6,6),因此基本事件总数为6×6=36个.而出现和为3的情况有两种:(1,2)与(2,1),故

二、“互斥”与“独立”混淆

例2 甲投篮命中率为0.8,乙投篮命中率为0.7,每人投3次,两人恰好都命中2次的概率是多少?

错解 记甲、乙两人投篮3次各命中2次分别为事件A、B,则“两人恰好都命中2次”为事件A+B.于是，P(A+B)=P(A)+P(B)=C230.82×0.2+C230.72×0.3=0.825.

分析 错解的原因是将事件A、B错误地认为是互斥事件,将两人恰好都命中2次理解为“甲恰好命中2次”与“乙恰好命中2次”的和来处理．

正解 记“甲、乙两人投篮各命中2次”分别为事件A、B,且A、B为相互独立事件,则“两人恰好都命中2次”为事件AB.于是，P(AB)=P(A)P(B)=C230.82×0.2×C230.72×0.3≈0.169.

三、“独立”与“不独立”混淆

例3 甲、乙两人参加历史知识竞答,共有10个不同的题目,其中选择题6个,判断题4个,甲、乙两人依次各抽取一题.

(1)甲抽到选择题、乙抽到判断题的概率是多少?

(2)甲、乙两人至少有一人抽取选择题的概率是多少?

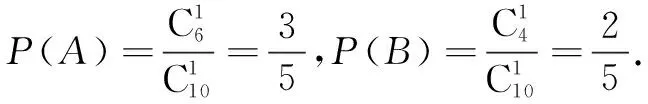
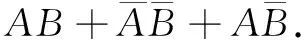
分析 错解是对独立事件概念模糊,将事件A、B错误地认为是独立事件,其实不然,甲先抽取一题后乙再抽取时样本空间已发生变化，甲抽到选择题与否对乙抽到判断题的概率是有影响的,故事件A、B不是相互独立事件．

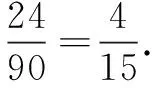
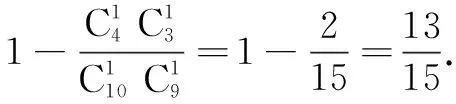
四、“有序”与“无序”混淆

例4 一个口袋中装有大小相同的2个白球和3个黑球,从中摸出一个球,放回后再摸出一个球,求两球恰好颜色不同的概率．

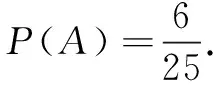
分析 由上面的摸球过程知摸球的过程是有序的,故两球恰好颜色不同要分先白球后黑球与先黑球后白球两种不同情况．

正解 记所求事件为A,则

五、抽样中的“放回”与“不放回”混淆

例5 一袋中有5个白球,3个黑球,从袋中连取三次,一次取一个,求下列事件的概率.

(1)若取后不放回,恰好取到一个黑球;

(2)若取后放回,恰好取到一个黑球.

错解 (1)记所求事件为A,由分步计数原理，可知取球方法共有8×7×6种,其中恰好取到一个黑球有C25C13种取法,故

(2)记所求为事件B,由分步计数原理，可知取球方法共有8×8×8种,其中恰好取到一个黑球有A25A13种取法,故

分析 问题(1)计算基本事件的总数考虑了抽取的顺序,而计算A含有的基本事件个数时没有考虑顺序,是用了组合的方法；同样，问题(2)计算所有的基本事件数时考虑了抽取的顺序,而计算B含有的基本事件个数时考虑顺序不够全面．

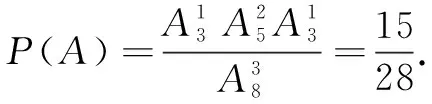
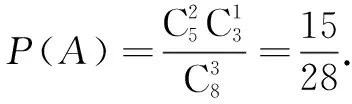
评注 不放回取球各次的取法不是相互独立的,故不可按独立事件同时发生的概率来计算，可以按等可能事件的概率来计算(如正解1).对不放回摸球来说，事件A=“不放回地逐个取k个球”与事件B=“一次任取k个球”的概率相等,即有P(A)=P(B).因此，不放回摸球通常可不考虑摸球顺序,按“一次任取k个球”的概率计算(如正解2).

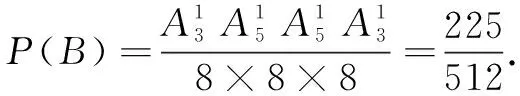
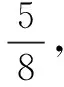
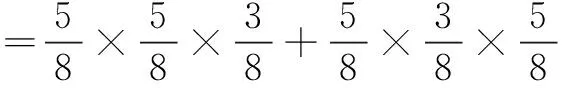
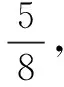
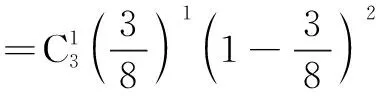
评注 放回摸球是指每次摸出一球后再放回袋中,下次再摸球时袋内球的总数不变;放回摸球可以按等可能事件的概率来计算(如正解1);放回摸球各次摸取是相互独立的,故可按独立事件同时发生的概率计算(如正解2);或按n次独立重复试验中某事件恰好发生k次的概率来计算(如正解3)．

六、“某事件发生k次”与“某事件在指定的k次发生”混淆

例7 一袋中装有大小完全相同的红球3个,白球6个,从袋中有放回地摸球,每次摸出一个,共摸5次,求:

(1)有3次摸到红球的概率;

(2)第一次、第三次、第五次摸到红球的概率．

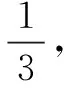
(2)记“第一次、第三次、第五次摸到红球”为事件B.当第一次、第三次、第五次摸到红球时,第二次、第四次摸到白球,故

分析 对问题(1)，错解是当成“有指定的3次摸到红球”与“有指定的2次摸到白球”来处理．实际上有3次摸到红球是“5次中的任意3次”与“指定的3次”是有本质上的区别．对问题(2)，错解是把“第二次、第四次指定为摸到白球”来处理．实际上第二次、第四次摸到的球可以是白球,也可以是红球,这两次可视为必然事件．

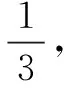
(2)记“第一次、第三次、第五次摸到红球”为事件B,则