发展运算能力 提升核心素养*

肖松柏 李 虹

(新疆乌鲁木齐市第四十一中学) (新疆乌鲁木齐市第十六中学)

《普通高中数学课程标准》(2017年版)明确提出数学运算是数学学科六大核心素养之一,不仅要考查学生的运算基本功,更重要的是要考查通过高中数学课程的学习,学生能进一步发展数学运算能力,有效借助数学运算解决实际问题．为此,《标准》指出数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养,其主要表现为理解运算对象,掌握运算法则,探究运算思路,选择运算方法,求得运算结果．基于此,在培养学生数学运算能力时，需要以上述理念为准绳开展．

一、对数学运算素养主要表现的理解

1. 理解运算对象是数学运算的前提

运算对象是指参与运算的各个数量及其关系．理解运算对象就是要对运算所涉及的概念和关系有清晰的把握,这样才能进行正确的计算．

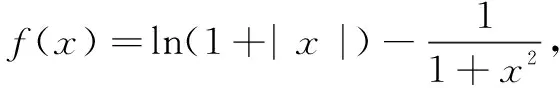
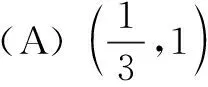
分析理解数学对象首先要理解运算对象有哪些?这些数学对象具有什么性质?它们在本题中是一种什么逻辑关系?本题中涉及的运算对象包括:含绝对值的函数、对数函数、反比例函数、抽象函数、复合函数、不等式、定义域等运算对象．它们在本题中形成了较为复杂的复合函数，与不等式结合为f(x)>f(2x-1)，这种无法直接计算的关系,是本题的解题难点．

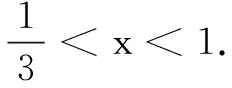
2. 掌握运算法则是正确数学运算的保障

运算法则是运算的依据,是推理的基础,也是运算实施的保障．在已知运算思路基础上,还要了解运算法则及适用范围,才能正确运算．

分析本题涉及的运算法则有:由Sn与an的关系求an,要清楚每一种运算法则的适用范围、意义和作用,准确掌握这些运算法则才能正确运算．

纵观本题所给条件,运算对象十分明确,由对任意n∈N*时k>Tn恒成立,转化求Tn的最大值,从而确定k的取值范围后再求k的最小值．

由4Sn=a2n+an-3(n∈N*)及n=1得a1=3．当n≥2时,由4Sn=a2n+an-3和4Sn-1=a2n-1+an-1-3相减得an-an-1=2,所以数列{an}是等差数列,从而an=2n+1．

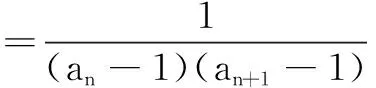
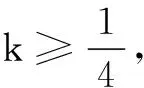
3. 探究运算思路是运用数学运算解决问题的关键

在问题研究对象和性质比较明确时,就需要思考运算过程的可能性和可行性．探究从哪里入手,利用什么运算,获得所求的结论．运算思路主要是识别运算顺序、选择运算法则、辨识运算对象、套用运算法则等．

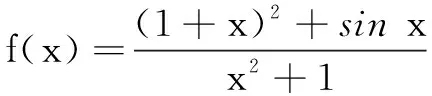
分析数学运算素养的水平划分水平三明确指出:在综合的情境中,能够把问题转化为运算问题,确定运算对象和运算法则,明确运算方向．本题作为2012年全国高考Ⅱ卷填空题的压轴题,就是将运算对象融入到一个综合情境中,要求根据问题的特征形成合适的运算思路．借助奇偶性函数的图象特征求最值,这与平时常见的利用函数图象、单调性、导数等常规方法有所不同,这就是本题的难点所在．本题要求函数f(x)的最大值和最小值,但具体怎样求思路不清楚．加之f(x)解析式太复杂，学生无从下手．一个自然的想法就是化简函数解析式,由此为突破口寻找运算思路．

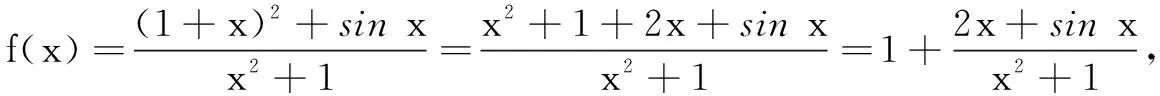
4. 合理运用运算方法是得出正确结果的有效途径

在明晰运算对象,形成运算思路,掌握运算法则后,能够针对运算问题,合理选择运算方法,设计运算程序,才能更好更快的解决问题．

例4(2018年新乡模考)已知等差数列{an}中,a1 012=3,S2 017=2017,则S2 020等于( )

(A) 2 020 (B)-2 020

(C)-4 040 (D) 4 040

分析数学运算是一种演绎推理,针对运算问题选择合适的运算方法是一种能力．同一个问题可能有不同的运算方法，通过比较,要选择运算步骤少、变形简单、运算量小等特点的最优的运算方法．一般先要掌握通性通法,当通性通法遇到困难或阻力,或正确完成一道题后,还要反思是否有其他的解法,是否有最优的解法．否则可能因为运算量大、运算繁、费时、费力还容易出错．

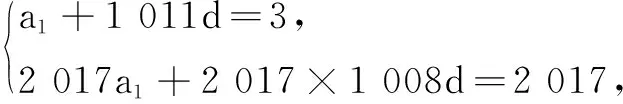
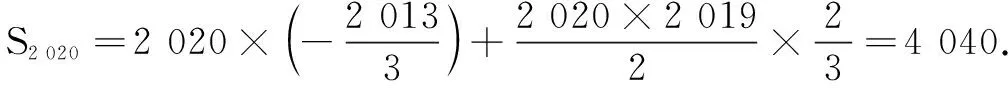
二、培养数学运算素养的教学建议

1.帮助学生掌握基础知识,适当记忆数学事实

任何数学运算都是伴随着数学概念而产生的,都是在概念系统中进行的．深刻理解概念是合理简捷地进行运算的前提．所以,运算能力要先从概念、性质、公式和法则的理解入手,学好有关运算的基础知识，是培养学生运算能力的前提与根本．另外,适当记忆一些数学事实也是非常必要的．比如,特殊角的三角函数值，函数图象的变换方法，圆锥曲线的相关公式，导数运算法则、指数、对数运算法则，常见题型的解决方法等.利用这些事实可以简化运算,提高运算效率．

2.进行科学系统的训练,培养良好运算习惯

对于运算训练,要选择有代表性的问题进行训练,要注意训练的科学性和系统性,要从简单到复杂逐步展开,要遵循“先慢后快”、“先模仿后灵活”的原则,要严格按照步骤进行运算，并能做到“步步有据”．通过对公式、法则的“顺用”、“逆用”、“变形用”的训练,在掌握通性通法的基础上，重视“简捷算法”和“一题多解”,帮助学生提高运算能力．当然,要注意训练“量”的把握,不能搞题海战、疲劳战,不能为了运算而运算．

3.注重数学思想方法在运算过程中的主导作用

运算中自觉运用数学思想方法,既有利于提高学生的思维水平,又有利于运算的合理简捷,从而提高运算的正确性和速度．数形结合、方程的思想、函数的思想等都是高中数学常用的思想方法,要记住常见题型的解决策略,灵活选择解题策略,发挥数学思想在运算中的主导作用．

总之,学生运算能力的提高不能靠速成,更不能靠题海战术.需要在平时的教学中注重思想方法的渗透,要让学生知道“怎样算”，“为什么这样算”．要从课堂训练,作业训练上下功夫,纠正运算习惯,做到合理控制运算步骤,采到得分点,努力达到“会算”、“算对”．