以问题为导向 引发学生深度思考——以“独立性检验的基本思路及其初步应用”教学为例

黄基荣 廖克杰

(广西南宁市第三中学，530201)

《普通高中数学课程标准》提出数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等六大数学核心素养.高中数学教材充分考虑了数学学科的基本特征和学生的认知规律,为“教”与“学”提供了很好的主题和内容,是实现高中数学课程目标、培养高中生数学核心素养的重要教学资源.“独立性检验的基本思路及其初步应用”蕴含着丰富的统计思想,有利于学生形成数学直观,增强基于数据表达现实问题的意识,是培养学生数学建模、数据分析等核心素养的理想教材.“问题是数学的心脏”,以问题为纽带,可以引发学生深度思考,从而思维得到有效锻炼.因此,本文以“独立性检验的基本思路及其初步应用”为例,谈谈在统计专题中以问题为导向,落实核心素养的认识与实践.

一、创设情境,引出问题

创设情境若以教师叙述为主,容易引发认知疲劳,不利于学生主动学习.因此以问题为载体,有利于激活学生的认知活力,让学生进行探究,主动思考、自然生长.

视频播放“美国烟民患肺癌去世,烟草公司被判236亿美元天价赔偿”，“韩国肺癌患者败诉,状告烟草公司赔偿无果”的新闻. 接着就以下问题与学生进行交流.

问题1两起案件中被告方申辩的主要依据是什么?

问题2要研究吸烟与患肺癌是否有关系,应收集哪几方面的数据?

设计意图通过真实法律案件激发学生的好奇心,为引入本课内容做准备,同时也强调了本节内容与实际生活紧密联系,体现了数学从生活中来又应用于生活的价值.

二、案例展示,初步体验

学生通过具体案例剖析,通过数与形直观感受“吸烟与患肺癌有关系”,使学生形成数学直观,在具体的情境中感知事物本质的能力.

为调查吸烟是否对患肺癌有影响,某肿瘤研究所随机地调查了9 965人,得到如下结果:

不患肺癌患肺癌总计 不吸烟7 775427 817 吸烟2 099492 148 总计9 874919 965

师生活动:教师引导学生用数学的眼光，观察统计表格的结构特点以及核心数据,介绍分类变量和2×2列联表的概念.组织学生讨论如下问题.

问题3请你用学过的统计知识来分析“吸烟与患肺癌是否有关”的数据,你能获得什么结论?

师生活动:学生利用频率分布表初步感知吸烟与患肺癌有关,教师用Excel表格作出等高条形图,引导学生分析图形的频率特征,直观体现两者的关系.

设计意图让学生体验读取、整理、分析和用数据说话的过程,体会统计的作用,进一步培养学生基于数据表达现实问题的意识.

三、勤于思考,探究新知

问题4你能有多大的把握认为”与患肺癌有关”？

教师先不急于引导,而是给学生留有充足的时间独立思考,接着小组合作探究,互相交流解决问题的方法. 直接研究两个分类变量有关比较困难,可以引导学生将问题转化为研究两个分类变量无关,即相互独立,引出独立性检验的思想.

假设H0:吸烟与患肺癌没有关系

用A表示不吸烟,B表示不患肺癌,则“吸烟与患肺癌没有关系”等价于“吸烟与患肺癌相互独立”,即假设H0等价于P(AB)=P(A)P(B).

设计意图前面通过频率分布表和等高条形图,学生已直观感受到了吸烟与患肺癌有关系,教师再引导学生运用相关概率知识分析吸烟与患肺癌之间关系的大小,由感性分析过渡到理性分析,体现数学的严谨性.

问题5如何表示P(AB)、P(A)和P(B)?在H0成立的条件下，你能得出什么结论?

师生活动:将数据一般化,用a,b,c,d来表示,得到如下列联表:

不患肺癌患肺癌总计 不吸烟aba+b 吸烟cdc+d 总计a+cb+da+b+c+d

学生以频率来代替概率,在假设H0成立的条件下推导得出ad≈bc.

问题6如何通过|ad-bc|的大小判定两个分类变量之间关系的大小?

学生:|ad-bc|越小,说明吸烟与患肺癌之间关系越弱;|ad-bc|越大,说明吸烟与患肺癌之间关系越强.

设计意图让学生通过“用频率估计概率”自主探究获得判断“两个分类变量之间关系的大小”的粗略方法,充分锻炼学生读取数据以及用数学的思维分析问题的能力,落实数据分析这一核心素养的培养.

问题7如何评判“大”和“小”的标准呢?

教师:在统计学中,为度量观测值与预期值的差值,1900年,英国著名的生物统计学家、应用数学家、科学哲学家皮尔逊(K.Pearson)引进了著名的卡方统计量:

(其中n=a+b+c+d为样本容量).

“卡方检验法” 提出后得到了广泛的应用,在现代统计理论中占有重要地位.

设计意图介绍K2公式的由来,在课堂上增加数学史内容,让学生感受数学发展的过程,体会数学的人文价值,提升学生学习数学的兴趣.

师生活动:教师引导学生观察随机变量K2公式的结构特点,然后给出K2的临界值表,加以解释,并简单介绍小概率事件的标准.

临界值表:

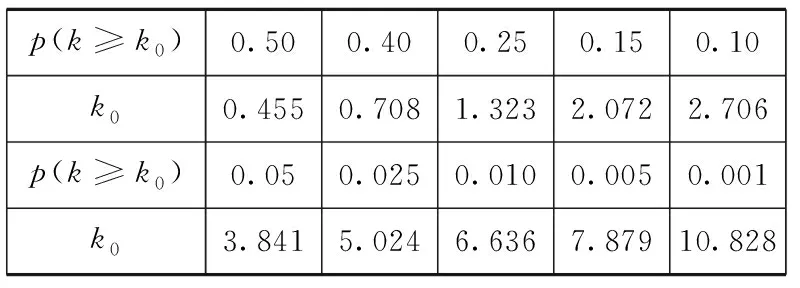
p(k≥k0)0.500.400.250.150.10 k00.4550.7081.3232.0722.706 p(k≥k0)0.050.0250.0100.0050.001 k03.8415.0246.6367.87910.828

问题8我们以k0=6.635为例,如何理解在H0成立的情况下,P(K2≥6.635)≈0.010的含义呢?

师生活动:教师提问,学生讨论、解释P(K2≥6.635)≈0.010体现的统计学意义,使学生明白:① 在H0成立的情况下,K2≥6.635的概率不到0.010,是一个小概率事件.若其发生,则可以否定H0成立,即认为吸烟与患肺癌有关系.② “H0成立”的概率不超过0.010.或者说判断“H0不成立”会犯错误,但犯错误的概率不会超过0.010.

让学生根据表格中的具体数据,动笔计算K2的观测值，其中

教师:如何快速计算上述式子?

部分学生能计算得到56.632,教师引导学生通过提取平方项的公因数,提高化简效率.在教学过程中强调算理意识,有效落实数学运算核心素养的培养.

教师:根据以上分析,请解释在H0成立的情况下,P(56.632≥6.635)≈0.010的含义.

学生1:“吸烟与患肺癌有关系”这种判断会犯错误,但犯错误的概率不会超过0.010.

学生2:我们有99%的把握认为“吸烟与患肺癌有关系”.

此时教师应当指出:对于实际问题,临界值的确定不能根据观测数据的结果,需要在获取观测数据之前确定.

设计意图把卡方临界值表提前讲述,使P(56.632≥6.635)≈0.010的引入更加符合逻辑,同时也更利于学生对独立性检验思想的理解.通过反复提问,让学生学会利用概率知识准确地对实际问题下统计学的结论,体会数学的严谨性,培养学生用数学的眼光观察世界和用数学的语言表达世界的素养.

四、理解运用,巩固练习

例1在某医院,因为患心脏病而住院的665名男性病人中,有214人秃顶,而另外772名不是因为患心脏病而住院的男性病人中有175人秃顶.

(1)利用图形判断秃顶与患心脏病是否有关;

(2)能否在犯错误的概率不超过0.01的前提下认为秃顶与患心脏病有关系?

练习:有甲乙两个班级进行一门课程的考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如下的列联表:

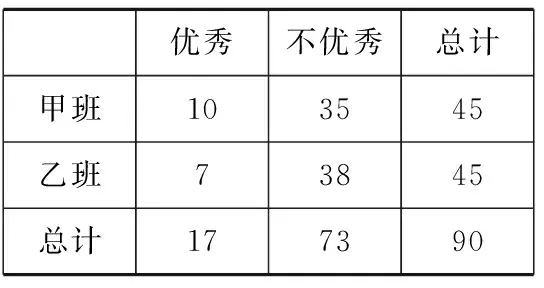
优秀不优秀总计 甲班103545 乙班73845 总计177390

请画出列联表的等高条形图,并通过图形判断成绩与班级是否有关系.根据列联表的独立性检验,能否在犯错误的概率不超过0.01 的前提下认为成绩与班级有关系?

设计意图让学生再次熟悉独立性检验的基本步骤,强调规范的书写过程,提升用数学的语言表达世界的素养.

五、总结反思,归纳提升

教师引导学生总结上述解决问题的过程,先让学生回答,然后教师再补充完善.

设计意图由具体问题总结得出判别“两个分类变量有关系”的一般方法,引出独立性检验的定义,让学生体会由特殊到一般的过程.

独立性检验定义:上面这种利用随机变量K2来判断“两个分类变量有关系”的方法,称为两个分类变量的独立性检验.

教师再次引导学生对判断两个分类变量是否相关的一般步骤进行总结,进一步加深对独立性检验的原理以及方法的理解:

① 给出假设H0:两个分类变量无关.② 计算K2的观测值k.③ 查表确定临界值k0.④ 作出判断:有(1-P(k≥k0))×100%的把握认为两个分类变量有关;或者说在犯错误的概率不超过P(k≥k0)的前提下,认为这两个分类变量有关.

问题9独立性检验的原理与反证法有什么区别和联系?

师生活动:学生总结,不断补充,最后教师完善.

设计意图与熟悉的方法进行比较,加深学生对独立性检验思想方法的理解与掌握,并且通过新旧知识的对比,帮助学生建立新旧知识的内在联系,完善知识结构.

教学设计通过“吸烟与患肺癌是否有关”典型案例的探究,了解独立性检验的基本思想、方法. 以问题为导向,遵循概念教学中的直观性、理解性、反面性原则去充分暴露概念的创造性过程. 让学生观察、思考,培养学生对数据的直观感受,体会统计方法的特点. 进一步地设置问题,引导学生经历数据处理的过程,体会运用数据分析解决实际问题的基本思想与方法,提高抽象概括能力和逻辑思维能力,培养学生用数学的眼光观察世界和用数学的语言表达世界的素养.