纯电动物流车最优制动能量回收控制策略研究
2020-04-28王茹洁武志斐
王茹洁,武志斐,邹 纯
(1.太原理工大学车辆工程系,山西 太原 030024;2.中北大学山西省先进制造重点实验室,山西 太原 030051)
1 引言
纯电动物流车是一种在城市广泛应用的新型运输车辆,由于行驶环境的特殊性,物流车制动较频繁,现有研究表明:在城市工况下,小型车辆在制动过程中消耗的能量约占总驱动能量的50%[1]。无线[2]分析了再生制动系统的可行性,试验研究表明加装制动系统的电动车在单次充满电后可提高行驶里程(5~20)%。
为解决试验车辆续驶里程不足问题,文献[3]基于复合控制策略,结合理想制动力I曲线与模糊控制对制动力进行优化分配,有效提升了电动汽车单次充满电后的行驶里程。文献[4]采用电机制动和带ABS的机械制动并联制动方式,得到能量回收效率为42.7%,但此方法复杂,只有改变制动状态才能回收能量。文献[5]将理想制动力I曲线和ECE法规结合进行制动力优化分配,可得出能量回收率为24%。文献[6]采用并行制动控制策略来优化分配制动力,得出能量回收率为15%。针对试验车,提出了最优制动能量回收策略,将其模型及整车模型分别在Matlab/Simulink和AVL cruise中建立,进行API联合仿真,验证了此策略的可行性。
2 基于最优制动能量回收控制的制动力分配
不同能量回收控制策略的最终目标都是增加续驶里程。为了达到目标,选取最优制动能量回收控制策略[7],需满足两个条件:一是满足所需的总制动力;二是需维持方向的稳定性。
汽车以一定减速度J减速制动时,前后轮制动力需满足下式:

式中:Fb—总制动力需求;Fbr—后轮总制动力;Fbf—前轮总制动力;Fbr-mech—后轮机械制动力;Fmt—后轮再生制动力。
车轮在制动过程中易出现抱死现象,导致制动时间延长,操纵稳定性丧失等安全问题。为避免这种现象的发生,在分配制动力时,应使其在I曲线附近,并且最低限度应大于ECE规程所规定的值。
3 基于有效发电功率最大化的电机工作点优化
电机处于发电状态时,其工作效率对有效发电功率产生一定作用,两者呈正比例关系。根据电机工作效率图知,电机发电过程中,同一转速对应的电机转矩值与工作效率呈非线性关系,如图1所示。
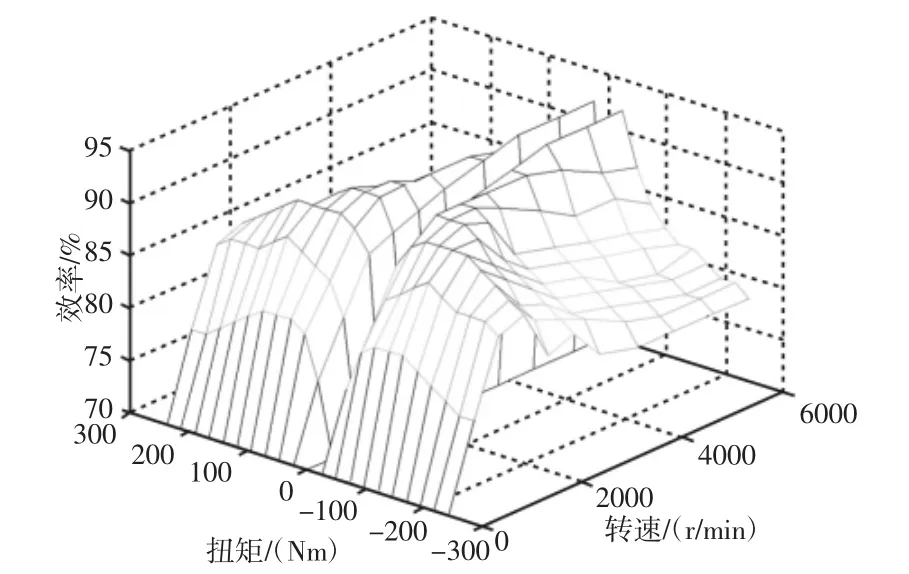
图1 电机效率图Fig.1 Motor Efficiency Diagram
在恒定转速5500r/min时,有效发电功率随着再生制动转矩的变化曲线,如图2所示。

图2 电机制动转矩对有效发电功率的影响Fig.2 Influence of Motor Braking Torque on Effective Power Generation
电机提供的转矩小于112N·m时,有效发电功率随着转矩的增大而非线性增加。在112N·m值处达到最大值,当超过112N·m时,电机的有效发电功率随转矩值的增大而非线性减小。因此可通过优化手段确定电机在一定转速下,有效发电功率达到最大值时的转矩值,该转矩对应的制动力即为最大再生制动力。
3.1 约束条件
电机最大再生制动转矩与转速n[8]有一定的函数关系,如下式:

式中:P—电机最大功率;n0—电机的基速;n—电机转速。
3.2 目标函数
电机的有效发电功率可通过式(4)求得:

式中:T—电机转矩;η—电机效率。
为得到最佳的制动能量回收效果,需最大化电机有效发电功率,优化的目标函数为:

式中:Pamax—电机允许最大发电功率;Pn—当前转速下允许的发电功率;Pcmax—电路允许最大发电功率。
η[9]定义:在选取的整个循环工况中,储能元件动力电池所回收并且存储的能量与整车动能变化量的比值,可通过式(6)求出:

式中:Ebat—动力电池回收的能量;ΔE—整车动能变化量;U—动力电池电压;I—动力电池电流;v1、v2—整车初始速度和末速度。
3.3 优化计算
在(500~6000)r/min范围内,以 500 r/min为间隔,选用粒子群优化算法[10]优化相应转速下电机最大有效发电功率对应的转矩值。在粒子群优化过程中,首先需要选取种群的个数,将种群的位置和更新速度初始化,获得初始局部最优值和全局最优值;然后根据式(7)的速度进化方式和式(8)的粒子进化方式进行粒子更新;最后通过公式计算并且逐步比较粒子的适应度,即可最终确定最佳粒子的位置,也就是最优解。
电机进行再生制动时,通过获得的最优解,利用最小二乘法,拟合出最大有效发电功率对应的电机转速与再生制动转矩的关系曲线,如图3所示。

图3 电机转速与转矩优化关系Fig.3 Optimal Relationship Between Motor Speed and Torque

式中:w—惯性权重;c1、c2—学习因子;p(K)—局部最优粒子位置;g(K)—全局最优粒子位置;rand()—介于[0,1]间随机数;x(K)—粒子当前位置。

一定转速下电机有效发电功率最大时,根据其对应的再生制动转矩计算出的最大制动力即为Fe,可通过式(9)求出:

式中:r—车轮半径;i—总传动比;η0—电动机到车轮的传动效率。
4 制动能量回收控制策略
制动力优化分配应尽可能在I曲线附近,其满足以下三个条件:(1)满足了附着条件的限制,以免车轮打滑;(2)能始终保持车辆的稳定性;(3)能保证前后轮同时抱死。I曲线通常,如式(10)所示:
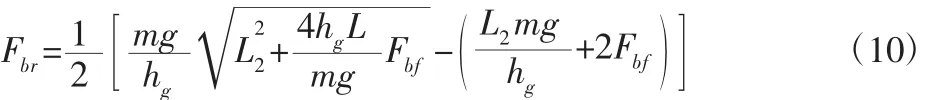
式中:m—汽车的重力;hg—质心高度;L2—质心到后轴的距离;L—车辆轴距;Fbf—前轮制动力;Fbr—后轮制动力。
ECE法规已分别针对货车、轿车提出了不同的制动力分配方法[11],试验车辆按货车的需求分配,边界方程为式(11):
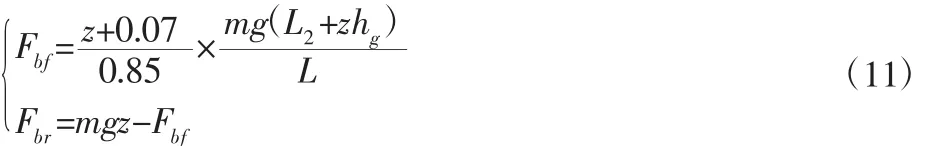
式中:z—制动强度。
f曲线表示前轮抱死时前后轮地面制动力之间的关系,如式(12)所示:

可行区域abdgk是由I曲线、φ=0.8的f线和ECE规程线共同组成,前后轮制动力必须在abdgk范围内,如图4所示。
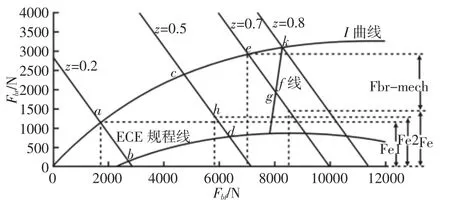
图4 前后轮制动力分布Fig.4 Distribution of Front and Rear Wheel Braking Force
试验用的纯电动物流车是后驱型,为了回收更多能量,应确保电机工作在有效发电功率最大值处,减少摩擦损失耗散大量能量。按此策略制动时的制动模式如下:(1)下长坡制动,制动过程是缓慢的,满足制动性能的总制动力较低,因此制动力仅依靠电机供给。(2)中轻度制动,满足制动性能所需的制动力适中,且大于最大再生制动力,不能仅依靠电机制动,应确保电机制动与机械制动协调配合。可按照最大再生制动力Fe所在区域分为三种情况,相同点是前轮制动力完全由机械制动力承担。Fe小于可行区域的最小值。如z=0.7时,可按线段eg分配,由图知,g点对应的纵坐标值小于Fe,因而按照e点分配前后轮的制动力。电机制动不能满足后轮需求时,其余不足部分由机械制动力承担;Fe在可行域范围之内。如z=0.5,可按线段cd分配,由图知最大再生制动力位于d点对应的纵坐标值与c点对应的纵坐标值之间,因而按照h点来分配前后轮的制动力。后轮全部由电机再生制动承担;Fe大于可行域的最大值。如z=0.2,可按线段ab分配,由图知a点对应的纵坐标值小于或等于Fe,因而按a点来分配前后轮的制动力。后轮全部由电机再生制动承担。(3)紧急制动,由于制动过程相当紧急,且受限于附着力,应按照k点来分配前后轮的制动力,并由机械制动力全部承担。
5 建模与仿真分析
5.1 制动能量回收控制策略模型与整车模型建立
根据前面提出的控制策略,在Simulink环境中建立控制模型,如图5所示。在AVL cruise中根据后驱试验车技术参数,建立整车模型,如图6所示。并将Simulink模型嵌入Matlab API模块中,对控制策略的有效性进行研究。

图5 Simulink控制模型Fig.5 Simulink Control Model

图6 制动能量回收整车模型Fig.6 Braking Energy Recovery Vehicle Model
5.2 仿真分析
选取适用于测试轻型载货汽车的UDDS城市运行工况进行仿真分析,如图7所示。并设置仿真初始SOC值为0.8,仿真结束后记录完整工况下的整车能耗以及制动回收能量,使用η对能量回收效果进行评价。同时,在UDDS工况下,SOC值由0.8下降到0.725,变化过程相对平缓,可得出试验车在整个工况下电池所回收的能量。此工况下动力电池SOC变化v如图8所示。试验车的能量消耗量以及所回收并储存的能量,如表1所示。在确保试验车保持制动方向稳定性的条件下,使用最优制动能量回收控制策略,使得制动力分配倾向于后轮,同时尽量确保电机工作在有效发电功率最大点处,由表1计算可得出在UDDC工况下有效回收率为28.71%。相比文献[5-6]得出的能量回收率24%、15%,上文采用的控制策略可以增加续驶里程。
图7 UDDS工况Fig.7 UDDS Operating Conditions
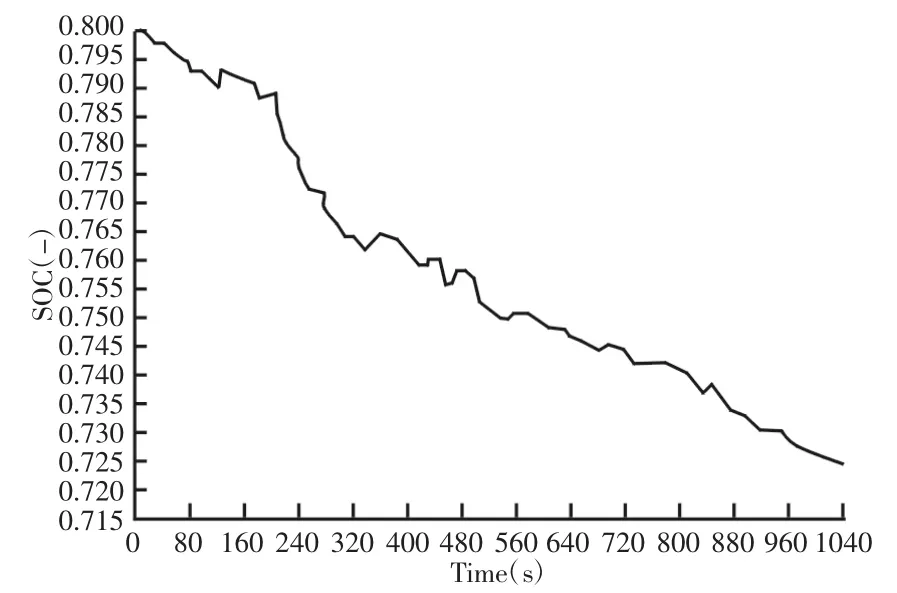
图8 SOC变化Fig.8 SOC Change

表1 能量回收效果Tab.1 Effect of Energy Recovery
6 结论
(1)针对试验用的后驱型纯电动物流车,基于最优制动能量回收控制策略,可以回收部分能量,验证了控制策略的可行性。(2)利用AVL cruise和Matlab/Simulink对机械制动力与再生制动力分配进行API联合仿真,结果分析出有效回收率达28.71%,续驶里程可以提高,回收效果显著。
