变截面涡旋盘的阿基米德螺线拟合方法
2020-04-28张春林
刘 涛,张春林
(兰州理工大学机电工程学院,甘肃 兰州 730050)
1 引言
涡旋压缩机由于其效率高,噪声低,质量轻,尺寸小,可靠性好等特点,被广泛运用于空调制冷、化工生产、动力等方面。为了追求高的行程容积和工作效率,涡旋压缩机的型线已从单一圆渐开线发展到多种基础曲线组合而成的组合型线。
目前数控机床只具备直线和圆弧插补功能,在实际的机械生产中加工诸如圆渐开线、高次曲线等非圆弧轮廓曲线时,若采用直线或圆弧拟合,要么具有较大的拟合误差,要么编程的难度与工作量较大,因此寻求一种新型的拟合方式势在必行。为了获得较高的加工精度和加工效率,在进行组合型线涡旋盘加工时,针对其型线的几何特性,利用阿基米德螺线进行拟合逼近,实现组合型线的高精度加工。
2 组合型线的分析
常见的组合型线有基圆渐开线—高次曲线—圆弧、基圆渐开线—圆弧—基圆渐开线。分析加工的组合型线由基圆渐开线、高次曲线、基圆渐开线三部分组成。
涡旋型线的数学模型:
(1)内壁
①第一段:圆渐开线

②第二段:高次曲线

(2)外壁
①第一段:圆渐开线

式中:r—第一段,第三段圆渐开线的基圆半径;Ror—回转半径;φ—展角变量;Rg—高次曲线的切向分量;Rs—高次曲线的法向分量。Ror=3.46,当r=3时,求得:

按照上述组合型线方程,得出的变截面涡旋盘的三维模型,如图1所示。
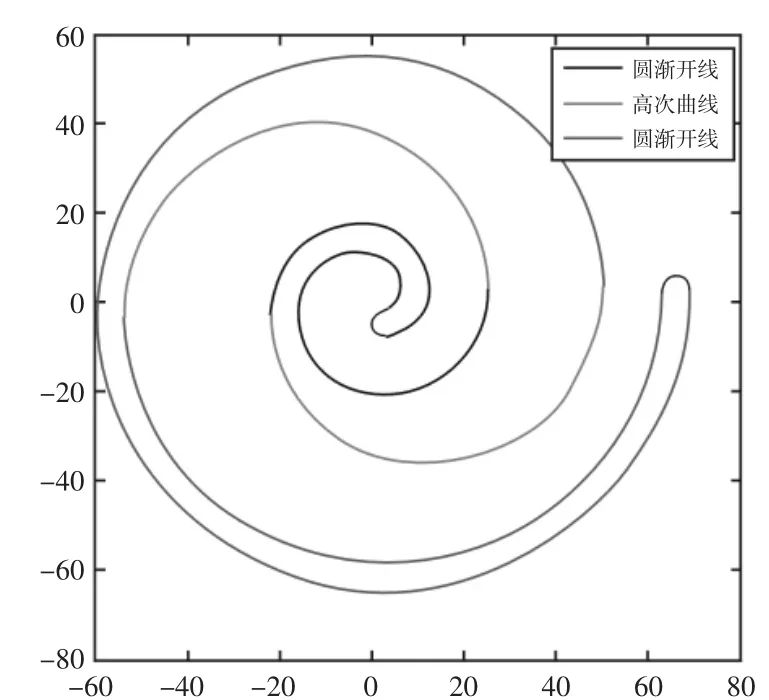
图1 组合型线涡旋盘Fig.1 Combined Line Vortex
3 阿基米德螺线拟合理论
3.1 阿基米德螺线方程
阿基米德螺线是一个点匀速离开一个固定点的同时又以固定的角速度绕该固定点转动而产生的轨迹。轨迹在极坐标下的方程:

式中:ρ0—曲线初始点的极半径;θ—曲线上任意一点的极角;v—常数。
3.2 拟合方法的介绍
阿基米德螺线拟合方法的基本思想是:对已给出的用函数表示的工件轮廓曲线,用一段方向与原曲线段相同的阿基米德螺线线段拟合该部分轮廓曲线,此段阿基米德螺线的中心为坐标原点。拟合曲线,如图2所示。

图2 阿基米德螺线逼近高次曲线Fig.2 The Archimedes Spiral Approximating High Curve Line
用阿基米德螺线逼近轮廓型线时,节点的数目及其坐标值取决于曲线的特性,逼近线段的形状与加工所允许的误差。在加工编程中既要求数控程序简洁,又要满足加工误差需求。为了节点计算简便,采用发生角等差值法,将曲线分成若干段,相邻两点的发生角相差Δφ,则:

式中:φi—第i个节点的发生角。假设高次曲线的起始点的发生角为φ0,结束点的发生角为φn,那么待拟合曲线段数目为:

由上式可知曲线段的数目n与发生角差值Δφ成反比,而Δφ的取值直接影响整个拟合过程的误差和数控编程的复杂性。故Δφ的取值要综合考虑选取。
3.3 拟合误差的计算
阿基米德螺线拟合方法所取得的阿基米德螺线段端点与Pi(xi,yi),Pi+1(xi+1,yi+1)重合,且凹凸方向一致,因此,在两个端点上不会存在拟合误差,拟合误差最大值一定发生在曲线中间位置,如图3所示。由于反三角函数的性质,型线上任意点Pi(xi,yi)在极坐标下的极角:

利用Pi(xi,yi),Pi+1(xi+1,yi+1)两点的坐标可以计算出两点的极角 θi、θi+1以及极半径 ρi、ρi+1,并由式(1)求出此段阿基米德螺线的方程:

假设高次曲线上任意一点P(x,y)的实际加工位置为P′,则此两点的极半径之差即为P点的拟合误差:

3.3.1 圆渐开线的拟合误差
由涡旋盘的组合型线方程可知,组合型线的第一段和第三段为圆渐开线,那么在此两段曲线中的任意一点的极角可依式(4)求得,但由于圆渐开线的特殊性,此处所需的极角即为圆渐开线的展角,因此极角与发生角的关系:

任意一点的极半径:
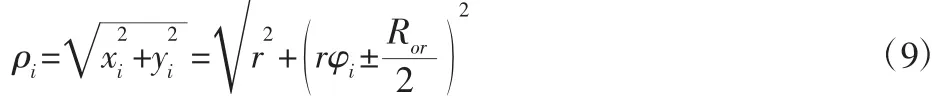
根据已给出的数学模型,取一段圆渐开线,Δφ即步长分别取0.01π,0.02π,0.03π,利用MATLAB软件对这几组不同的取值进行拟合误差的计算,得到的曲线,如图3所示。
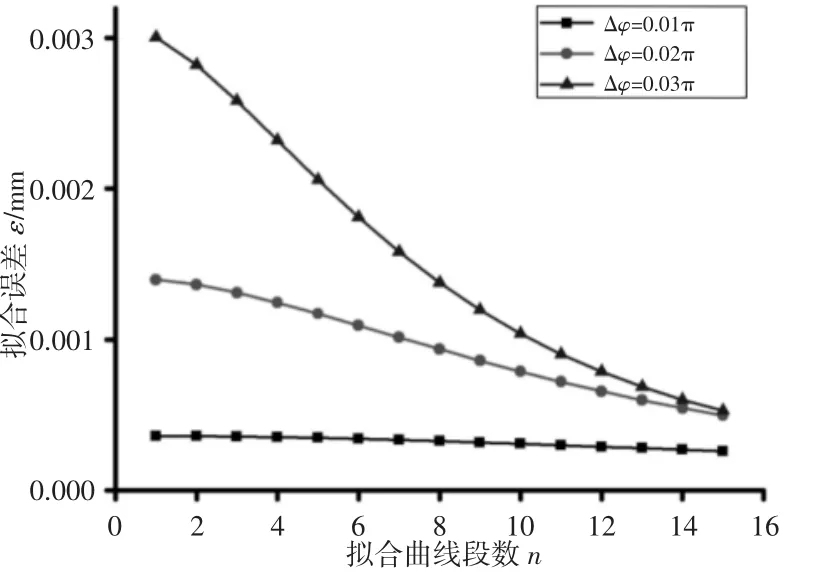
图3 圆渐开线插补节点间误差Fig.3 Error of Interpolation Nodes of Circle Involute
3.3.2 高次曲线的拟合误差
由涡旋盘的组合型线方程可知,组合型线的第二段为高次曲线,那么在此曲线中的任意一点的极角由式(4)求得。
任意一点的极半径:
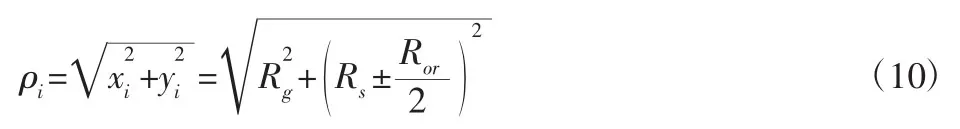
如拟合圆渐开线,取一段高次曲线,步长Δφ分别取0.01π,0.02π,0.03π,利用MATLAB软件对这几组不同的取值进行拟合误差的计算,得到的曲线,如图4所示。

图4 高次曲线插补节点间误差Fig.4 Error of Interpolation Nodes of High Order Curve
观察图3和图4可得:当使用阿基米德螺线等Δφ的方法逼近圆渐开线与高次曲线时,无论Δφ取值如何,拟合误差均随发生角的增加而减小,换言之,高次曲线的极半径越大,拟合误差越小,整个型线中最大拟合误差出现在初始曲线段。所以只需将初始曲线段的拟合误差控制在误差允许范围内,整个曲线的拟合便可满足加工精度的要求。根据以上讨论,得出Δφ的取值流程,如图5所示。
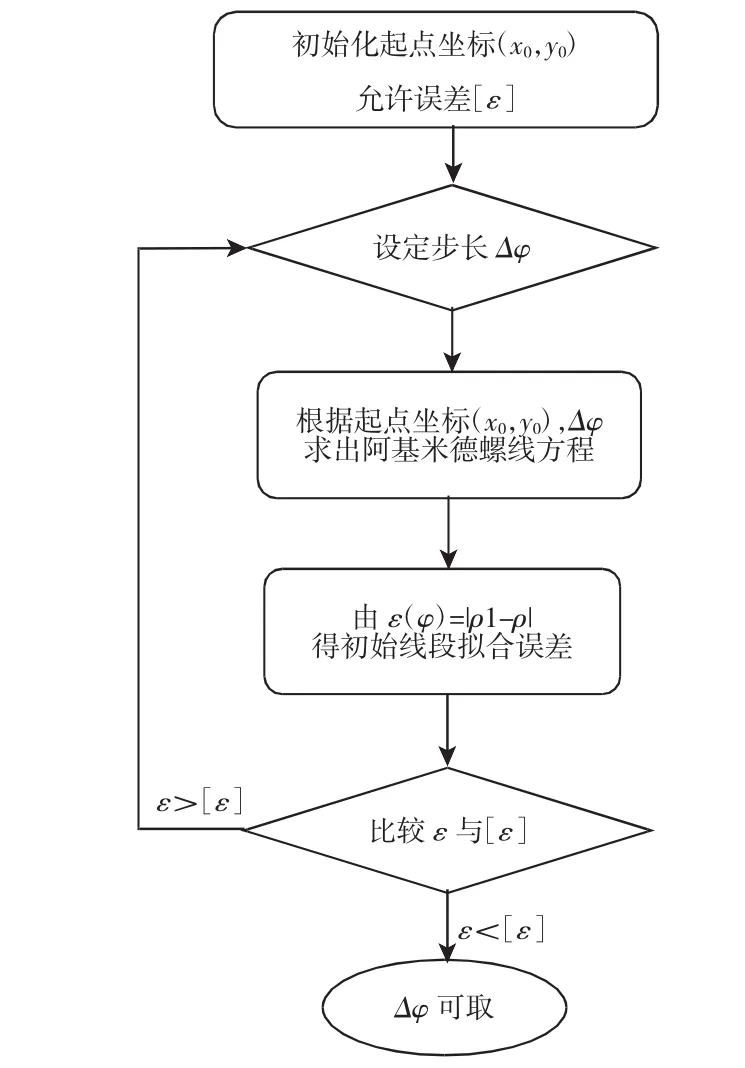
图5 Δφ取值流程图Fig.5 Flow Chart of Δφ Values
4 应用实例
根据阿基米德螺线的形成原理,在实际数控加工中,只需工件在自转的同时以相应的速度进行水平方向上的移动。工件自转的角度为相邻两节点在极坐标下的极角差值,工件水平移动的距离即为相邻两节点的极半径差值。
4.1 拟合圆渐开线
根据已给出的组合涡旋型线方程,取外壁第一段型线即圆渐开线作为待拟合曲线,设定基于阿基米德螺线拟合方法拟合的最大允许误差[ε]<0.001mm,按Δφ取值流程图所示方法求得Δφ即步长 Δφ=0.252rad。
按数控加工的要求,利用步长0.252rad将该段圆渐开线划分为若干曲线段,根据阿基米德螺线拟合的原理进行拟合误差的计算,并用直线和圆弧拟合所有曲线段,得到相应的拟合误差,如表1所示。
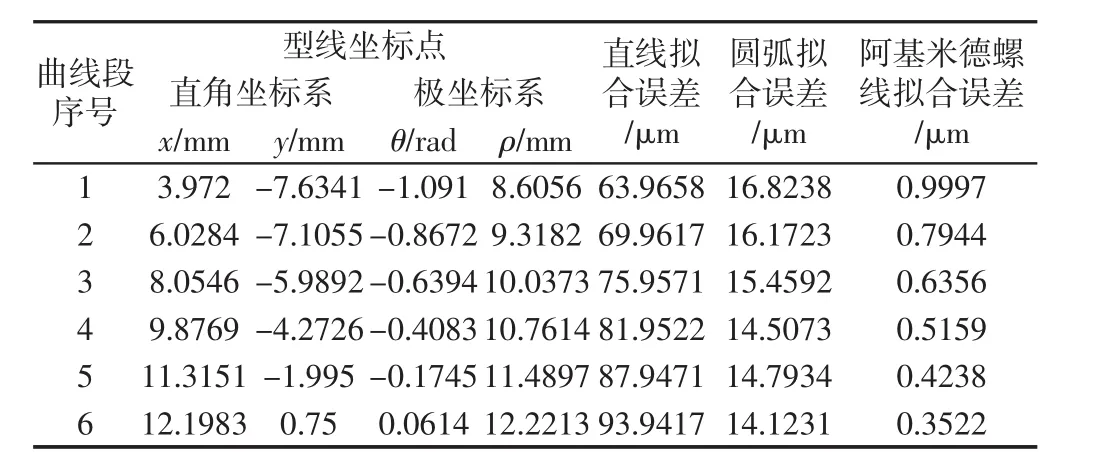
表1 圆渐开线拟合误差Tab.1 Fitting Error of the Involute
4.2 拟合高次曲线
与拟合圆渐开线方法类似,用阿基米德螺线、直线、圆弧分别拟合内壁第二段型线即高次曲线段,设定基于阿基米德螺线拟合方法的最大允许误差[ε]<0.001mm,得步长Δφ=0.022rad。计算得到的高次曲线拟合误差数据表,如表2所示。

表2 高次曲线拟合误差Tab.2 Fitting Error of High Order Curve
表1和表2中的数据表示所有曲线段的最大误差所在位置及三种拟合方式的拟合误差。从表中的数据可以看出基于阿基米德螺线拟合方法的拟合效果最好,两段型线拟合误差均小于1μm,拟合圆渐开线过程中,直线拟合和圆弧拟合最大误差分别达到93.9417μm和14.1231μm;拟合高次曲线过程中,直线拟合和圆弧拟合最大误差分别达到2.1971μm和1.4153μm。
在满足[ε]<0.001mm的情况下,计算出涡旋型线上所有节点,直线插补需要14654个点,圆弧插补需要1542个点,同等要求下,阿基米德螺线拟合节点总数只有430个,比直线拟合少90%,比圆弧拟合少70%。尤其拟合第三段型线过程中,只需要将其外壁型线分为6段,内壁型线分为3段,这是直线和圆弧拟合方法都不具备的。可见阿基米德螺线拟合方式所需的节点更少,拟合误差更小,拟合效果更好。
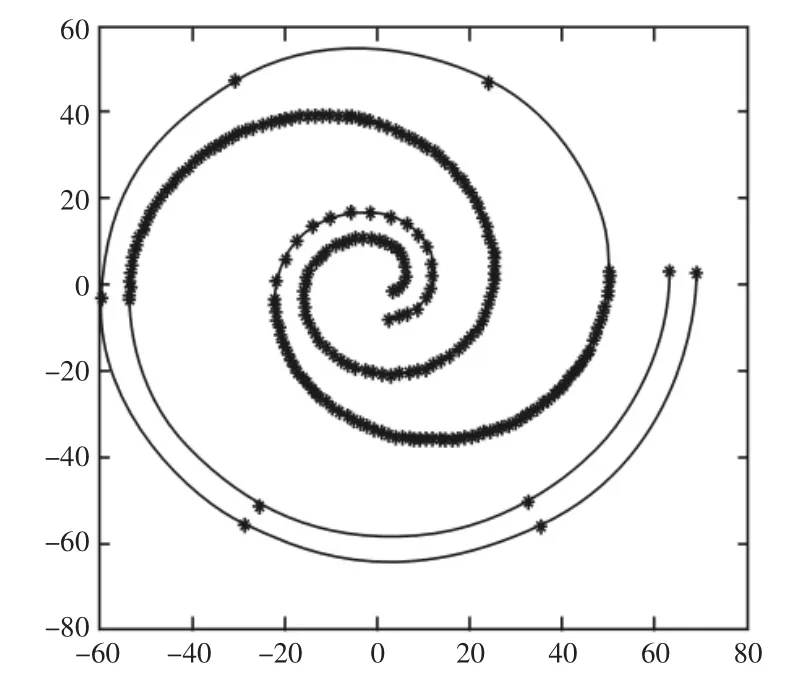
图6 拟合节点Fig.6 Fitting Nodes
5 结论
提出基于阿基米德螺线逼近圆渐开线—高次曲线—圆渐开线组合涡旋型线的方法与流程,并将其与直线拟合、圆弧拟合方法进行了对比,得到如下结论:
(1)相较于目前两种成熟直线和圆弧的拟合方法,阿基米德螺线拟合可以更好地逼近加工曲线,采用这种加工拟合方式可以使刀具轨迹光滑,拟合节点数少,加工精度和效率高;
(2)相较于拟合高次曲线,利用阿基米德螺线拟合外圈大展角圆渐开线时所需插补节点数更少,优势更为明显;
(3)根据拟合全程型线误差变化的规律,在加工型线过程中适当地进行干预,适当增大步长,可显著提高加工效率。
