算思结合突破困难提升素养——以一道解析几何题求解历程为例

宋秀云

(江苏省新海高级中学 222006)

日前笔者所在学校高三的一次月考结束后，很多学生都觉得自己考“爆”了.原来是试卷中涉及解析几何的解答题没能处理好，耽误了时间，影响了学生的考试状态，导致整份试卷没有做好.很多时候遇到解析几何问题，一部分学生纠结的是明明知道选择的处理方法可能不是最佳方案，但理论上“应该”能解决问题，却苦于繁琐的运算而纷纷止步，导致解析几何题不能彻底解决；还有一部分学生总想回避繁琐的计算、找捷径，一旦考场上找不到更好的方案便失去信心，加之平时运算训练不到位，在繁杂的运算面前便无从下手，只能望运算而兴叹，最终以失败而告终.教学中我们应该如何突破这一瓶颈？笔者认为教师应该带领学生直面困难、算思结合、解决问题，在突破困难的过程中进一步优化问题解决的方案，提高学生解析几何问题的处理能力，进而提升学生的数学运算等方面的素养.

1 寻考场解答之惑

(1)求椭圆C的方程；

(2)设Q为△PF1F2的内心，

①当x0=-3时，求点Q的坐标；

②求证：点Q在定椭圆上.

笔者阅卷时注意到大部分学生的答案是这样的：

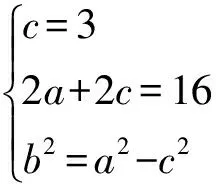
(2)

直线PF1:x=-3，直线PF2:8x+15y-24=0，

设Q(x,y)，则点Q到△PF1F2三边的距离相等，

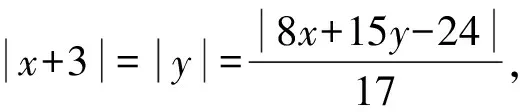
由于点Q在△PF1F2内部，

所以x+3>0,y>0,8x+15y-24<0，

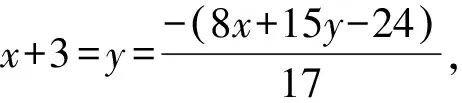
图一

②直线PF1:y0x-(x0+3)y+3y0=0，

直线PF2:y0x-(x0-3)y-3y0=0，

则点Q到△PF1F2三边的距离相等，即

绝大多数同学都写到这里进行不下去了.

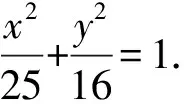
对于学生卡壳的问题，笔者询问学生原因，学生如是说：点Q位置没定，不论采用讨论或是平方去绝对值，运算量都太大，另外分母还有根式，不敢做下去……

2 研试题讲评之道

经过充分的调研，在试卷讲评课上，笔者便带领学生从问题出发，直面困难，寻求解决策略.对于学生遇到的分母中出现的根式问题，借助椭圆方程便可轻松化解，即

对于学生担心而不敢尝试的分子绝对值讨论问题，课上组织学生进行了尝试与深度的思考.

2.1 突破困难，提升对线性规划问题的理解

图二

图三

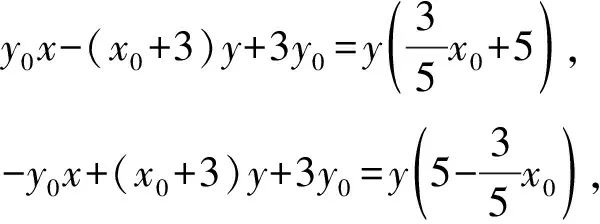
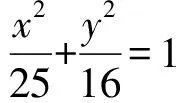
学生对于自己解答过程中卡住的问题得以解决，非常兴奋，同时也反思：遇到问题要敢于尝试，不能因自己预见的各种“隐形”的困难，停止解决问题的脚步.此时有一位同学站起来提出自己的想法：本题直线PF1与直线PF2方程Ax+By+C=1中我们都在纠结B的符号没定，去讨论点Q是在直线上方还是下方，相应去绝对值，如果我们注意到A的符号是确定的，点Q始终是在直线PF1的右侧、PF2的左侧，从而一定有y0x-(x0+3)y+3y0>0、y0x-(x0-3)y-3y0<0便可轻松解题.话音刚落，点赞声此起彼伏.变与不变本身就是一对矛盾，换一个视角理解线性规划问题，对于本题绝对值带来的“麻烦”来说无疑是柳暗花明！

2.2 调整方案，感受向量加法几何意义的作用

“内心还是角平分线的交点，能否求出其中两条角平分线的交点，直接解出点Q的轨迹？” 学生提出了自己的想法.我们一起来试试.(直接处理动点Q的情形) 确定角平分线的方程是解决问题的关键. 例如如何确定直线F1Q的方程？问题归结到只需确定直线F1Q的斜率即可.经过讨论，同学们给出了如下方法：

图四

设P(x0,y0)，F1(-3,0),F2(3,0),

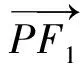
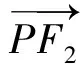
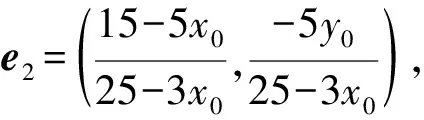
则e3=(1,0),

联立直线F1Q,F2Q得

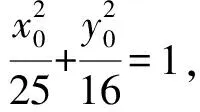
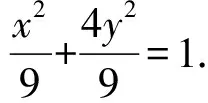
直线F1Q是角平分线所在的直线，借助向量加法的几何意义，构造菱形，求两向量和，利用方向向量得到直线斜率，写出两条角平分线的方程，使用交轨法求点Q的轨迹，综合向量知识，问题解决过程提升了学生的思维品质与运算能力.

2.3 优化转译，体会角平分线性质的妙处

“计算两条直线的方向向量、求直线的交点运算较为复杂.能否不求交点坐标，借助角平分线的性质解决本题呢？”问题刚提出，同学们立刻进入了思考状态，纷纷尝试能否从这个角度突破难题.

很快便有同学提出自己的想法：

延长PQ交F1F2于点M,

过Q作QE⊥F1F2于点E,

过P作PH⊥F1F2于点H,

设P(x0,y0)，Q(x,y),M(m,0),

F1(-3,0),F2(3,0),

图五

(1)

(*)

(2)

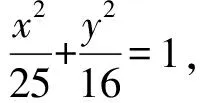
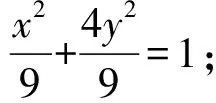
将内心条件转译，借助角平分线的性质，通过作垂线、焦半径公式将长度关系转化为纵坐标、横坐标的关系，三思后行，回避繁琐运算，思维深刻、方法巧妙、深刻理解问题的几何背景.

2.4 深度思考，挖掘内切圆圆心的隐含信息

通过以上思考，学生渐入佳境，又有同学提出借助切线长相等解决问题：

设P(x0,y0)，Q(x,y),

F1T-F2T=PF1-PF2，

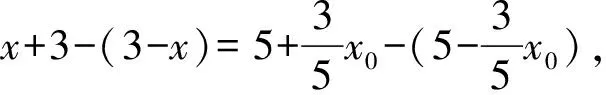
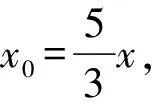
图六

设PS=m，则PF1+PF2=2m+2c=2a，

即m+c=a，所以m=5-3=2，

在Rt△PQS中，(x-x0)2+(y-y0)2=4+y2，

点Q既为内心，作出三角形的内切圆，“无中生有”，挖掘内切圆的半径及切线长相等等隐含的几何信息，充分利用图形的几何特征助力代数运算，节约运算成本，事半功倍.

还有同学提出：如果设Q为△PF1F2的旁心，点Q是否在定椭圆上？

3 悟解析教学之理

解析几何是沟通代数与几何的纽带，为我们探究几何问题提供了新的角度，即用代数方法准确刻画图形的位置关系.但是代数方法的运算量往往比较大，目前的高中学生数学运算能力普遍比较弱，特别是带式子的整式运算.而解析几何对学生的运算能力要求又比较高，含字母比较多，有时“会却算不出”.这就要求我们在研究几何问题时，引导学生直面困难，求解过程要学会算思结合，逢山开路，遇水搭桥.既要会从代数角度运算，也要学生会观察图形特征；既要能直接“硬算”，也要会选择“方法”简算；既要能选好求解切入点，又要会中途调整方向、追根溯源、优化解法、把握本质. 解题中因思考而行动，因行动而理解，因理解而优化，促进解析几何中代数与几何的综合能力的升级与发展.

3.1 算思结合 突破困难

高考中，解析几何作为解答题通常是学生成绩的一个分界点，很大程度上决定了学生成绩能否跃上新的台阶.“算”作为解析几何的重要特征，对学生的能力要求很高，主要体现在方法的选择与运算路径的设置上.方法一中，学生常用的转化内心条件的方法即到三边距离相等，遇到了去绝对值的麻烦，学生尚未“开战”便被自己假想的“敌人”打倒了，这便是对于选择的方法没有进一步深思的原因.课上教师带领学生思考去绝对值的方法，深度理解了线性规划问题，以思促算，突破了学生考场上的困难.方法二，是直接求点Q的坐标，很多学生考场上没有选择该方法的原因是没有找到合理路径表示直线F1Q的斜率.课上学生进一步思考，从向量的角度，结合角平分线的角色定位，借助向量加法的几何意义，通过单位向量表达直线的方向向量即斜率，算思并举，提升了学生综合运用知识的能力，也使得学生能想到的“朴素方法”得以顺利实施.平时的教学中，教师要充分意识到算与思之间的关系，深研问题，剖析不同学生的运算层次与水平，引领学生算思结合，设计运算路径，规划解题方案，突破解题过程中的困难.

3.2 调整优化 提升素养

解析几何归根结底研究的还是几何问题.思考所研究的对象的几何背景，挖掘几何背景所蕴含的代数特征，并尝试将其代数化，寻找具体模型的解题突破口.解题过程中，几何背景的深度挖掘，图形特征的充分利用，以思助算，优化运算思路、调整解题路径，能大幅度减少复杂的运算，提高运算的效率与准确率，促进学生运算素养与高阶思维的提升.方法三，将内心的条件转译为角平分线的交点，转而思考角平分线的性质，将角平分线的几何特征即分线段所成比代数化，并将其借助坐标表示出来.方法四，挖掘内心所对应的三角形的内切圆，综合使用椭圆的定义、焦半径公式代数化切线长相等这一几何特征，算思并举，克服困难. 这两种方法与方法二对比，多思少算，另辟蹊径，以简驭繁，大大提高了问题解决的效度.课堂上，学生在复杂问题情境中，经过严谨的有逻辑的思考，明晰条件之间的关联，建立数与形的联系. 整个过程中学生通过直观形象、逻辑推理、代数运算，交流、讨论、调整，探索、优化解决问题的新思路，提高了学生的思维品质，学生充分感悟解析几何中所蕴含的思想方法，切实提高了学生分析问题、解决问题的能力.