裂项法教学的几点思考

王 蕊 梁 栋

(天津市武清区杨村第一中学 301700)

《普通高中数学课程标准(2017年版)》指出：“通过高中数学课程的学习，学生能获得进一步学习以及未来发展所必需的数学基础知识、基本技能、基本思想、基本活动经验(简称‘四基’)；提高从数学的角度发现和提出问题的能力、分析和解决问题的能力(简称‘四能’)．”[1]因此，数学方法的教学，不能以数学方法的应用作为唯一的教学目标，应立足问题解决的全过程，真正落实“四基”、发展“四能”，最终提升学生的数学学科素养．事实上，裂项法的学习过程蕴含着丰富的启迪学生思维的资源．下面笔者谈谈自己的几点思考．

1 从概念和公式推导过程了解裂项法

人教社A版教材中是用归纳猜想的方式得到等差数列通项公式的，除此之外，教学中，多数教师会给出下面的方法：

由等差数列的定义，可知

a2-a1=d，a3-a2=d，…，an-an-1=d，上面等式两边分别相加，得an-a1=(n-1)d，

所以an=a1+(n-1)d．

这种方法难度不大，学生不存在理解上的困难，同时还能加深学生对等差数列定义的理解，体会数学概念在解决问题中的应用．这种方法实质是裂项法，即把公差d“裂”为an-an-1，然后求一个每项都是d的常数列的前n-1项和，最后得到等差数列的通项公式．常见的用裂项法求和的题目，数列通项是已知的，“裂”的结果是确定的．等差数列通项公式推导过程中，an是未知的，求和也不是解题目标，而是通过求和得到计算an的公式．但二者采用的方法是相同的，都是通过“裂”和“求和”得到结果．从这个意义上说，等差数列通项公式的推导方法就是裂项法，从这个推导过程认识裂项法，简单自然，以此作为学习裂项法的起点，符合学生的认知基础和思维习惯．

等比数列前n项和公式的推导方法也是裂项法．我们具体分析一下．

教材中是这样推导的：

一般地，对等比数列a1，a2，a3，…，an，…，它的前n项和是Sn=a1+a2+a3+…+an，根据等比数列的通项公式，上式可写成

Sn=a1+a1q+a1q2+…+a1qn-1．

①

我们发现，如果用q乘①的两边，可得

qSn=a1q+a1q2+a1q3+…+a1qn，

②

①②的右边有很多相同的项，用①的两边分别减去②的两边，就可以消去这些相同的项，得

(1-q)Sn=a1-a1qn，

当q≠1时，等比数列的前n项和公式为

“①的两边分别减去②的两边，就可以消去这些相同的项”，我们把这些消去的项保留下来，便可发现

(1-q)Sn=(a1-a1q)+(a1q-a1q2)+(a1q2-a1q3)+…+(a1qn-1-a1qn)，

当q≠1时，等式两边同除以1-q，得

考虑到教学目标的达成和教学重点的突出，在推导等差数列通项公式和等比数列前n项和公式时，推导过程中包含的裂项法的思想不必向学生说明，但在引入裂项法时，结合这些推导过程进行分析，有助于培养学生发现和提出问题的能力．

2 通过an与Sn的关系理解裂项法

数列{an}能否用裂项法求其前n项和，要看是否存在数列{bn}，满足an=bn+1-bn，其中n∈N*．任意给定一个数列{an}，设Sn是其前n项和，则有an=Sn-Sn-1(n∈N*，n≥2)，这个等式表明，an可以“裂”为Sn-Sn-1，即给出了bn的一个结果：bn=Sn-1(n≥2)．由此可知，只要给出一个Sn，由等式an=Sn-Sn-1就可以得到一个可用裂项法求和的数列．例如，

给定Sn=2n+1-1，则Sn-Sn-1=(2n+1-1)-(2n-1)=2n+1-2n=2n，n≥2．

这样，可将2n“裂”为2n+1-2n，用裂项法求等比数列{2n}的前n项和．

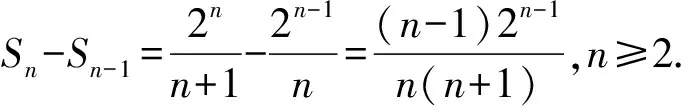
用裂项法求数列{an}的前n项和．

给定Sn，由an=Sn-Sn-1得到an后，可适当对an的表达式变形，加大或降低问题的难度，最后得到用裂项法求和的数列问题．对学生而言，他们只知道an，不知道Sn，是已知an求Sn，这无疑是个难点．在这个过程中，要以锻炼学生的观察、猜想能力为目标，通过对各种形式“裂”的结果的探究，积累必要的数学活动经验．

如果问题难度较大，学生的解题过程不会太顺利，即使学生知道an由Sn-Sn-1得到，但还原出这一结果也是很困难的，因此，教师要尽可能多给出“新颖”的Sn，让学生体验不同形式“裂”的结果，逐渐悟出其中的规律，思考时有所遵循．

设m是常数，由an=Sn-Sn-1=(Sn+m)-(Sn-1+m)，可知an“裂”的结果并不唯一．

3 通过数列相邻两项的运算发现裂项法

裂项法的核心是“裂”，找到“裂”的结果就等于问题得到了解决，由于“裂”的结果是一个数列相邻两项之差，因此教学中可以引导学生观察一些数列相邻两项之差，发现“裂”的特征．

从求数列前n项和的角度看，对等差数列{an}，

这是用裂项法求等比数列的前n项和，其实质和教材中的方法是相同的．

qn-1-qn=qn-1(1-q)也可以看成两个数列{qn-1}和{qn}对应项的差．

对等差数列{n}和等比数列{qn-1}，研究它们对应项的积，得到新的数列{nqn-1}，这是典型的“错位相减法”的模型．进一步，考察数列{nqn-1}相邻两项的差，

(n+1)qn-nqn-1=nqn+qn-nqn-1

=(q-1)nqn-1+qn,

于是有(q-1)nqn-1=(n+1)qn-nqn-1-qn．

这个等式虽不是一般意义上“裂”的形式，但仍可用来求数列{nqn-1}的前n项和，其思想和裂项法相同．如果求数列{nqn}的前n项和，只需在上面等式两边同乘q即可．

思维的起点是思维过程中最重要的一个环节，是学生思维生长、发展的基础．通过研究一个数列相邻两项的差，目的不是为获取“裂”的结果，而是让学生体验发现的过程，总结“裂”的规律，发现更多有价值的结论，消除对裂项法的神秘感，提高发现问题的能力，为应用裂项法提供思考的基础．在这个过程中，学生会体会到数学方法不是凭空飞出来的，而是有它出现的必然性和自然性．在积累了一定的经验之后，面对具体问题时，就知道如何通过猜测和尝试寻找“裂”的结果，在一定程度上解决“为什么这样想”的问题，即解决思维起点的问题．

有了(q-1)nqn-1=(n+1)qn-nqn-1-qn，很自然地提出问题：nqn-1能不能“裂”呢？如果能，“裂”的结果具有什么特点？

观察等式两边，发现如果能“裂”，很可能是nqn-1=[a(n+1)+b]qn-(an+b)qn-1的形式，a，b如果存在，可用待定系数法确定．

上面等式整理得，n=(aq-a)n+aq+bq-b，

所以aq-a=1，aq+bq-b=0，

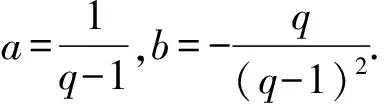
这样就得到了nqn-1“裂”的结果，即

从体验过程、积累经验，到观察猜想、尝试验证，是学生对裂项法从记忆模仿到灵活运用的过程．在这个过程中，对学生思维起决定作用的不是裂项法的解题套路，而是裂项法的思想．另一方面，我们经常强调要暴露解决问题的思维过程，目的是使学生学会思考，而不是记忆简单的结论．然而，思维结果和思维过程是密不可分的，思维过程取决于思维方向，思维方向指向思维结果．没有思维结果，思维过程也就无从谈起，每一个思维过程都是由若干思维结果构成的，思维结果是新的思维过程的基础，因此，在向学生展示思维过程的同时，还要关注思维结果，结果与过程有机融合，教学效益才能最大化．研究数列相邻两项之差，既是一种探索的过程，也包含对结果的深入思考．

4 从数学方法间的联系中提高运用裂项法的能力

数学知识、方法之间有着千丝万缕的联系，学生学习数学知识、方法也不是一次完成的，因此，教师要把数学知识、方法的教学放在整个高中数学的背景下系统处理，这就要求教师具备揭示数学各部分内容之间内在联系的意识，具有挖掘数学知识、方法间相互联系的方法，进而提出富有思维深度的数学问题，为学生数学学习创设优质的问题情境，促进学生领悟数学思想，提升解决问题的能力．

裂项法和数学归纳法有着密切的联系．举个例子，用数学归纳法证明：

证明过程中有下面的步骤：假设n=k时等式成立，即

那么n=k+1时，有

把上面最后一行的中间步骤去掉，

③

凸n边形内角和等于(n-2)π，其中n≥3，这是用数学归纳法证明的一个典型题目．借鉴数学归纳法的证明方法，可以用裂项法证明．

设凸n边形内角和为an(n≥3)．如图，考察凸k+1边形A1A2…Ak+1(k≥3)，连结Ak-1Ak+1，

则凸k+1边形A1A2…Ak+1的内角和等于凸k边形A1A2…Ak-1Ak+1内角和加△Ak-1AkAk+1

的内角和，又△Ak-1AkAk+1的内角和等于π，于是有ak+1=ak+π，即ak+1-ak=π．

分别令k=3，4，…，n-1(n≥4)，

由ak+1-ak=π，得

a4-a3=π，a5-a4=π，…，an-an-1=π，

上面不等式两边分别相加，得an-a3=(n-3)π，

所以an=(n-3)π+a3．

因为a3=π，

所以an=(n-2)π，n≥4．

又a3=π满足an=(n-2)π，

所以an=(n-2)π，n≥3．

上述证明方法和等差数列通项公式推导方法是相同的．由ak+1-ak=π可知，a3，a4，a5，…，an是公差为π的等差数列，用等差数列的通项公式可直接得出结论．就本题的证明而言，采用数学归纳法和裂项法效果是相同的，但从思维的角度看，差别还是很大的，因为即使不知道(n-2)π这个结论，用裂项法也能推出这个结论，而数学归纳法则是知道结论的前提下进行证明．当然，先归纳猜想结论，再用数学归纳法证明是另外的问题．

最后指出，虽然等差数列和等比数列的前n项和公式也可以用裂项法求得，但教材中的方法简单易懂且直观性较强，又蕴含数学文化的教育元素，教学中应以教材中的方法为重点．随着学习的深入，可适当引导学生用裂项法去探索证明的方法．考虑到课标的要求，以上关于裂项法的内容，不一定全向学生介绍，而应根据教学实际，在必要的时候，有选择地让学生探究．