考虑不同路面附着情况的整车质量估计方法研究
2020-04-23黎佳骏王博钟国旗唐寿星卢萍萍
黎佳骏,王博,钟国旗,唐寿星,卢萍萍
(1.广州汽车集团股份有限公司汽车工程研究院,广东广州510000;2.吉林大学汽车仿真与控制国家重点实验室,吉林长春130022)
整车质量估计功能的设计对于无人驾驶控制 系统的准确性、车辆操纵的稳定和安全性、车辆燃油经济性等多个方面有重要的意义。通过实时在线估计整车质量,车辆控制器可利用更精准的模型对复杂、高度非线性的车辆运动过程进行控制。例如,在商用重载货车的控制中,受货物重量的影响,货车的整车质量变动范围较大,如果控制算法使用恒定的质量常数,则会在货车质量发生较大变动时,难以给出符合实际工况的刹车、油门、转向等控制指令,无法保持较高的控制精度,甚至在某些特殊、极端的工况下产生脱离预定轨迹、倾覆等严重的后果。对于整车质量估计这一问题,国内外学者开展了大量研究[1-8]。不同的研究通常根据不同的车辆动力学特性,利用不同的传感器,再结合特定的滤波或优化算法对整车质量进行求解。国外研究起步较早,文献[1]给出了不同的估计方法以适应2种不同传感器组合,推导了在最差情况下的估计误差边界,并利用扩展卡尔曼滤波(extended Kalman filter,EKF)实现质量估计。文献[2-3]利用双遗忘因子的递归最小二乘法(recursive least square,RLS)对整车质量和道路坡度同时估计,详细分析了在实际使用过程中常规RLS算法可能出现的问题,并设计了独特的损失函数,引入可独立调整的双遗忘因子,避免了RLS算法可能出现的震荡问题。文献[4]设计了基于观测器的质量/坡度估计方法,借助滑模量在存在驱动力矩和车辆速度的情况下,实现对参数的在线估计。国内学者也进行了大量相关研究,取得了丰硕的成果。文献[5]利用电动车纵向驱动力信息较为准确的特性,采用驱动力和纵向加速度中的高频部分对整车质量使用RLS 进行估计,在此基础上利用运动学、动力学融合观测的方法实现对道路坡度的估计,取得了良好的实验结果。文献[6]建立了双离合变速器的动力学模型,利用卡尔曼滤波算法估计变速器输出的转矩大小,然后利用RLS实现对整车质量和道路坡度的估计。文献[7]利用前向欧拉法获得车辆纵向动力学模型的系统状态空间形式,进一步对非线性过程方程进行线性化,获得了过程方程的雅阁比矩阵,最后利用EKF实现了对质量和坡度的同时估计。
利用车辆纵向动力学模型进行建模并实现整车质量估计过程中,估计结果会受到路面附着特性的影响,特别是在对车辆牵引力进行计算的过程中,当车辆运行在低附着路面时,较大的车轮滑转会使估计结果包含较大误差。上述研究中,少有论文探讨路面附着情况对整车质量估计过程的影响,因此考虑通过调整质量估计模型,引入路面特征系数,使估计模型适应不同的路面附着情况,初步解决不同路面附着特性对质量估计的影响,在仿真环境中验证所实现方法的有效性。此外,多数论文均在获得车辆的纵向动力学方程后,利用卡尔曼滤波算法或递推最小二乘算法及其各种改进形式进行质量或者坡度的估计。文中通过公式推导说明卡尔曼滤波方法和递推最小二乘方法两者之间的内在联系。
1 考虑路面附着的质量辨识
车辆在纵向上的受力情况如图1 所示。根据车辆受力平衡原理可得[8]:

式中:Ft为车辆牵引力;Fair为车辆行驶过程中所受的空气阻力;Froll为轮胎滚动引起的滚动阻力;Finerital为轮胎旋转产生的惯性力的纵向等效力;mgsinβ为存在坡度时重力在沿坡面方向的分力;ma为车辆纵向的惯性力;Fsys为无法直观建模的系统误差。车辆牵引力的求解过程如下:
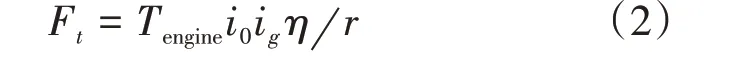
式中:Tengine为发动输出扭矩;i0ig为传动系统传动比;η为传动效率;r为轮胎半径。考虑到试验中可直接获取参数类型,Ft计算过程为

式中:ωengine为发动机转速;v为车辆纵向运动速度。由式(3)可知,驱动力完全利用发动机的输出状态进行估计,未考虑轮地接触情况。因此引入路面特征系数γ对牵引力进行调整,式(1)转化为
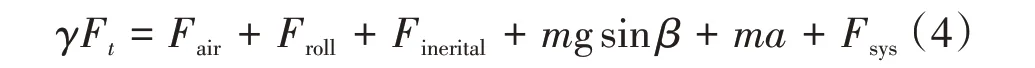

图1 车辆纵向受力情况图
γ可看作是关于车轮滑转率s和路面材质等状况φ的非线性函数,与利用附着系数不同,路面特征系数直接作用在发动机输出转矩上,使得对发动机输出转矩的计算更为精确。工程应用中可通过试验标定的方式获得参数表,在求解质量时,通过查表方式获得车辆当前运动状态下的γ;也可通过设计相应的识别方式[9-10]获得γ。Fair的计算过程为
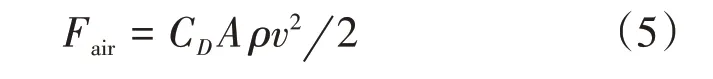
式中:CD为空气阻力系数;A为迎风面积;ρ为空气密度。Froll的计算过程为

式中:f为滚动阻力系数。Finerital的计算过程为

式中:Iw为轮胎的转动惯量。将式(2)~(7)代入式(4)并分离与质量m无关的量,移项后得
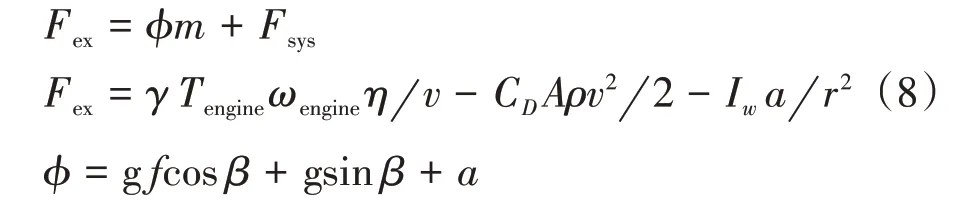
将式(8)写成向量相乘的形式,并添加估计误差ei:
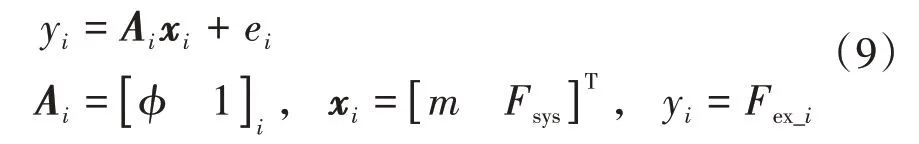
式中,待求系数xi可以直接利用不同方法估计;yi为标量形式,在后续推导式(10)中,为了不失一般性,写作矩阵形式,此时式(9)中yi可视作一行一列的特殊矩阵。
2 估计方法
2.1 递推最小二乘
考虑系统模型式(9),当数据不断从外部传入时,在(k+1)时刻有
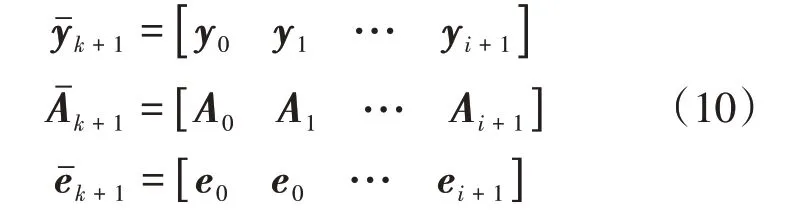
引入
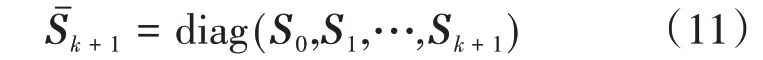
式中:Si为m维正定赫尔米特矩阵。递推最小二乘优化目标为
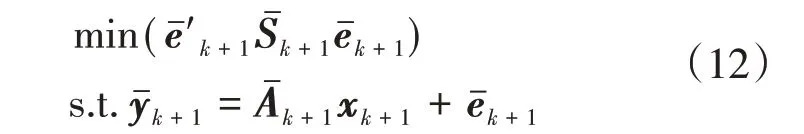
求解结果为
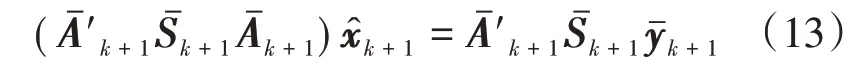
写为求和的形式:

令
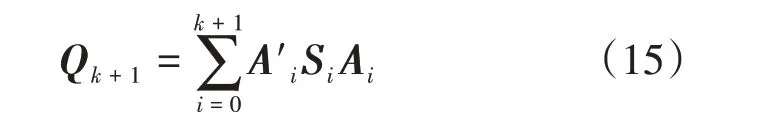
写成递推形式:
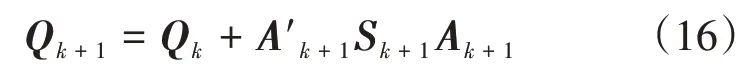
利用式(16)化简式(14)可得:
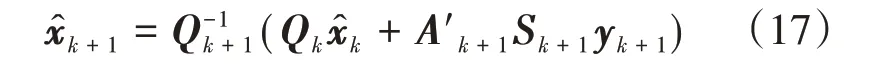
将式(16)左右同时乘以x̂k,并将式(14)代入得
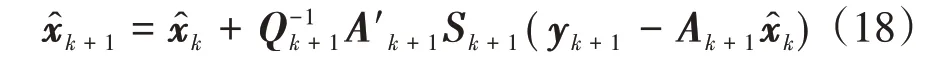
令

将式(17)右侧求逆的形式展开:

结合式(18)和式(19)实现对式(9)中待求整车质量参数的估计。
2.2 卡尔曼滤波
图2展示了卡尔曼滤波方法的计算步骤,递推最小二乘可采用相同的步骤进行计算。
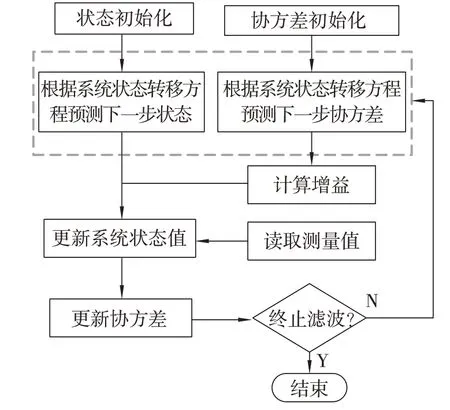
图2 卡尔曼滤波方法计算流程
标准的卡尔曼滤波器可写成预测部分:
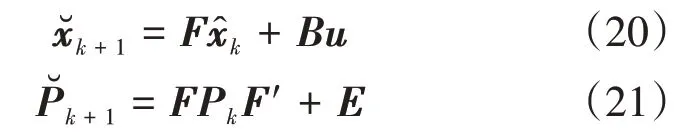
和更新部分:

对于预测部分,取F= I,B= 0,u= 0,E= 0,得

对于更新部分,将式(22)和式(26)代入式(23)得

将式(27)两侧乘以(HPkH'+ I),展开、移项,得

将式(27)再次代入式(28)右侧,并令H=Ak+1,得
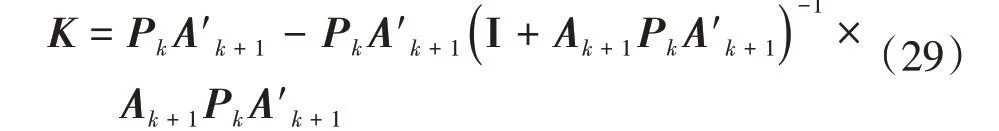
将式(29)和式(18)~(19)进行比照,可见:
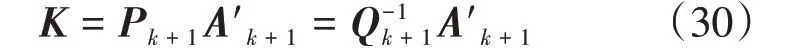
当Sk+1= I 时,式(25)与式(18)等价。将式(27)代入式(24),令R= I,同时将式(26)代入,化简可得:
将H=Ak+1代入式(31)可见,式(24)与式(19)有相同的形式。至此完成了递推最小二乘法和卡尔曼滤波的推导并进行了关键等式的一致性比照。
通过推导可看出:卡尔曼滤波中的式(24)和式(25)分别与递推最小二乘法中的式(19)和式(18)有相同的形式。因此递推最小二乘法是无输入(u= 0)且状态转移矩阵为单位矩阵(F= I)的卡尔曼滤波特殊形式,2种方式均可估计出整车质量。
3 数值模拟
采用CarMaker 对整车质量估计方法进行测试,利用Matlab/Simulink进行整车质量辨识模块代码编写,实现CarMaker/Simulink 联合仿真。在Simulink 中编写仿真模块如图3 所示,模块包含空气阻力计算、牵引力计算、惯性力计算和加速度项计算子模块,通过递推最小二乘法估计获得整车质量。在CarMaker 中搭建带有不同坡度不同曲率的道路场景,使用的车辆模型为某型号电动车。
由于递推最小二乘和卡尔曼滤波算法的一致性,因此选用带有遗忘因子的递推最小二乘方法。遗忘因子对应式(12)中的S,同时对应卡尔曼滤波中式(22)的R。算法中所涉及参数取值如表1所示。

图3 Simulink计算过程图
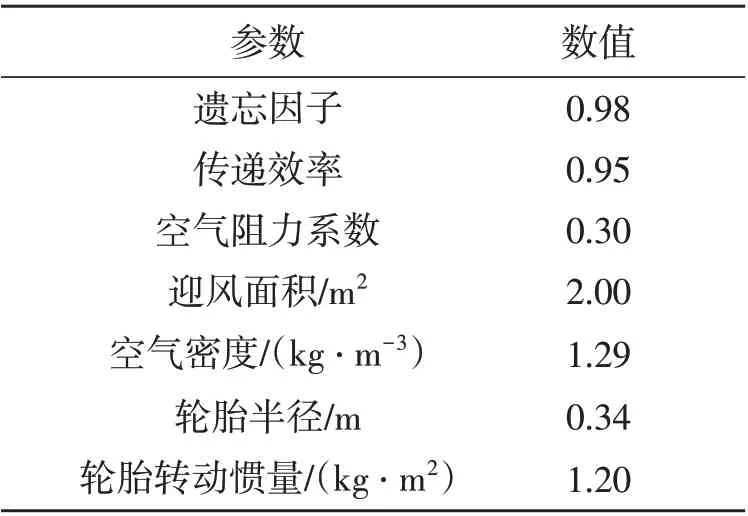
表1 算法涉及参数表
3.1 考虑路面附着情况仿真结果
对考虑路面附着和未考虑路面附着2 种情况进行测试。考虑路面附着的情况下,使用的系统模型如式(4)所示;未考虑路面附着的情况下,使用的系统模型如式(1)所示。仿真过程中,减小路面的摩擦系数,造成车轮可能存在较大滑移率的情况,以此确认考虑路面附着的质量估计算法的作用。
在CarMaker环境中将道路分为连续的2段,第1段道路的路面摩擦系数为0.7,第2段道路的路面摩擦系数为0.2,设置车辆的运动速度为60km·h-1,车辆在第1段道路上运动约40 s后进入第2段低附着道路,得到的仿真结果曲线如图4 所示。从图4中可以看出,在未考虑路面附着的情况下,整车质量的估计结果并不稳定,在40 s附近出现了估计质量和估计误差的巨大变化,估计质量大幅偏离真实值;而在考虑路面附着的情况下,通过控制路面特征系数,使得质量估计过程更为稳定,在40 s 附近出现了估计质量的小幅偏移,偏移后能较快回到真实值附近。
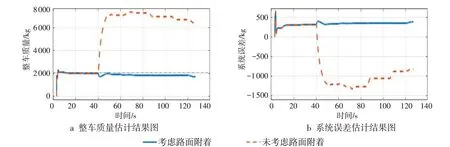
图4 考虑及未考虑路面附着情况仿真结果图
3.2 不同整车质量估计结果
选取不同的整车质量对算法进行测试,改变整车质量的方法是在CarMaker 中添加载荷,考虑到现实场景中正常行驶的车辆无法短时间内大幅改变自身的质量,因此通过分步添加载荷改变整车质量,和现实中改变整车质量的方式类似。图5 a 展示了该算法对不同整车质量进行估计的情况,可以看出:经过一段时间的运行后,质量估计算法的输出结果收敛到整车质量真实值附近,收敛速度较快,且能保证估计值的稳定。
图5b给出当质量估计输出稳定时估计值和真实值之间的差异程度对比,从准确程度上看:当整车质量为1 770 kg 时,质量估计误差小于1%;当整车质量为2070kg时,质量估计误差小于5%。当整车质量增大时,质量估计误差随之增大。质量估计的误差值始终保持在10%的范围之内。
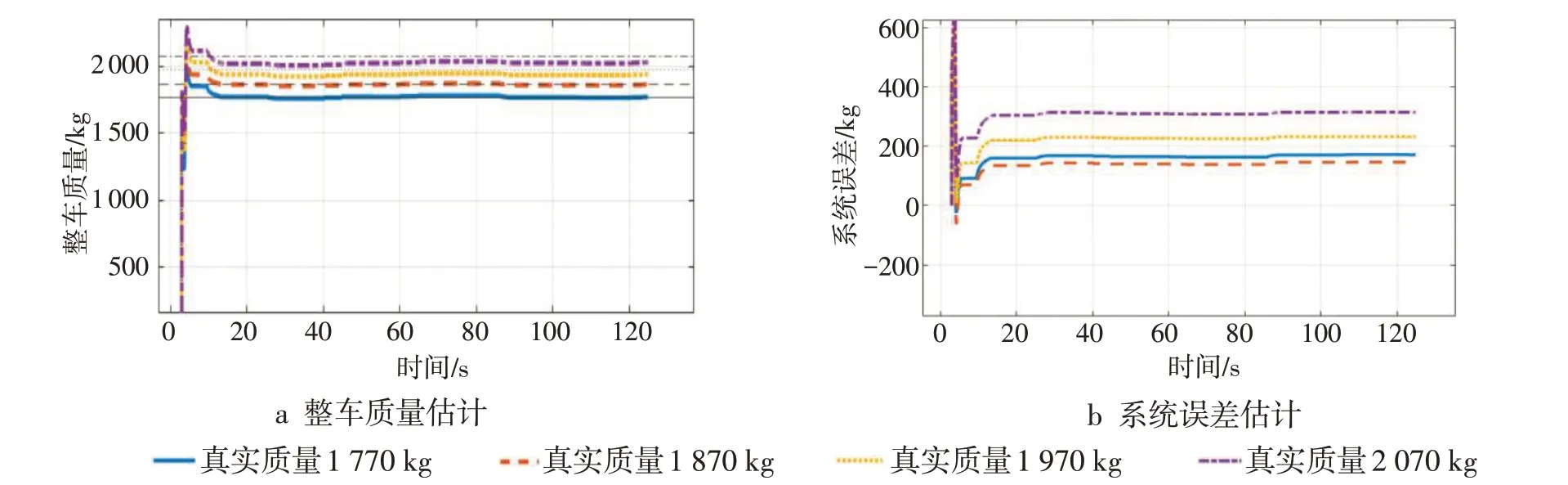
图5 不同整车质量及系统误差估计结果图
表2 给出了整车质量估计稳定输出的误差情况,可以看出:计算出的系统误差稳定值随着整车质量真实值的增加而增大,直观解释是当整车质量增加时轮胎与地面之间的接触过程变得更为复杂,许多未建模的作用力在车辆所受的总外力中占比增大,导致质量估计算法求解出更大的系统误差来平衡未建模的作用力对质量估计过程的影响。
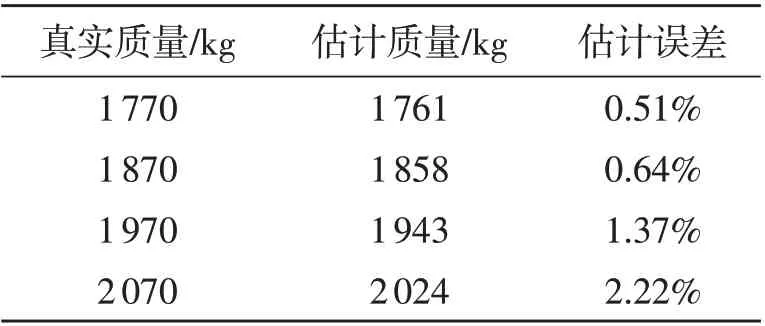
表2 整车质量估计误差表
4 结论
1)通过引入路面特征系数,考虑路面附着的整车质量估计方法能适应更多的路面附着状况,在路面附着系数较小的情况下,能稳定完成质量估计过程。后续结合路面特征系数在线辨识方法可实现更精准的质量估计。
2)算法在一定范围内的质量变动下,对整车质量的估计的稳态误差稳定在10%范围之内。
3)递推最小二乘估计的特定形式可以看作是状态转移矩阵为单位矩阵的卡尔曼滤波估计,对工程实践有借鉴意义。
