微裂纹群损伤的超声非线性评价数值仿真
2020-04-23朱建新吕宝林王小岩
乔 松,朱建新,吕宝林,王小岩
(1.合肥通用机械研究院有限公司,国家压力容器与管道安全工程技术研究中心, 合肥 230031;2.合肥通用机械研究院特种设备检验站有限公司,合肥 230031;3.中国机械设备工程股份有限公司,北京 100055)
材料劣化过程表现为微裂纹的成核、长大,直到宏观裂纹形成而导致结构失效,微裂纹与破坏机理之间存在密切关系[1]。作为材料微观和细观层面的缺陷,微裂纹在材料加工制造阶段几乎不可避免,即使微裂纹尺寸在微米量级,但是受载情况下裂纹尖端的应力集中仍然是不可忽视的潜在隐患[2]。
传统线性超声检测技术在微观裂纹检测方面有明显的局限性[3]。研究表明材料早期性能退化阶段占据材料疲劳寿命期的80%90%[4]。近年来,力学、声学和材料学领域的一些研究发现,材料性能退化总是伴随着某种形式的材料力学行为,从而引起超声波在固体材料中传播的非线性[5]。
固体材料中微裂纹引起的非线性声源,其基本特点是接触界面上非线性应力-应变关系引起了超声波非线性特征,反映了材料内部局部缺陷对超声信号的影响。
国内外学者关于超声非线性效应开展了大量研究。RICHARDSON[6]研究了超声波作用下光滑界面开闭运动变化引起的超声非线性特征,并通过理论解释了界面上产生的倍频、分频等谐波成分。ACHENBACH等[7]求解了微裂纹张开位移和应力场的关系,以及裂纹张开位移和谐波之间的关系。HIROSE等[8]采用边界元的方法研究了裂纹接触面产生高次谐波的应力方程。KIM等[9]提出一种微机械模型以描述两种固体界面的弹塑性接触与裂纹开闭非线性特征以评估接触面质量。MEZIL等[10]利用低频激励波与高频调制波同时激励待测构件,通过提取非线性混频波旁瓣特征对裂纹进行成像分析。
阎红娟等[11]基于微裂纹非线性弹簧模型,给出二阶相对非线性系数与微裂纹形状尺寸的关系。吴斌等[12]通过有限元计算了微裂纹长度和数量与非线性系数的一般关系。贾俊等[13]建立了用非线性振动-声场调制指数表征裂纹尺寸的数学模型,并提出了裂纹张开和闭合应力的在线测量方法。赵友选等[14]基于随机分布表面微裂纹模型,采用有限元方法计算了非线性系数与裂纹密度的关系。焦敬品等[15]通过仿真计算了裂纹方向对散射场的影响,通过反射波与裂纹方向变化关系提出一种微裂纹方向测量方法。
目前公开文献中的研究对象主要是单一裂纹,且裂纹长度大于超声波半波长的情况。超声波通过裂纹的方式为透射,笔者选择长度小于半波长,随机分布的微裂纹群为研究对象,通过有限元仿真分析方法,计算微裂纹群的超声非线性效应,分析微裂纹数量对超声非线性系数的影响,以及裂纹衍射效应与超声非线性特征间的相互作用。
1 基本理论
微裂纹导致的结构有效拉伸/压缩弹性模量非对称现象会使得结构拉伸/压缩响应不同,从而引起纵波变形产生高阶谐波[16]。
接触非线性导致的应力σ和应变ε的关系,可采用积分形式表示,如式(1),(2)所示。
(1)
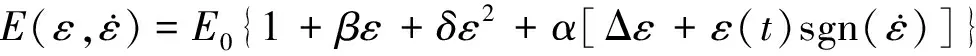
(2)
采用逐级近似法求解,仅考虑二阶非线性,一维纵波在各向同性材料中的传播波动方程(为坐标x和时间t的函数)如式(3)所示。
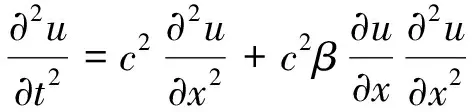
(3)
式中:c为波速。
假设单频率余弦声波频率激励下,方程的解为
u(x,t)=u(0)+βu(1)
(4)
根据非线性波动方程,式(3)的近似解为
u(x,t)≈A0sin(kx-ωt)+
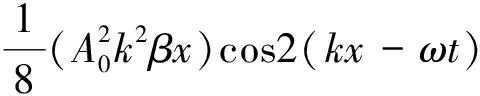
(5)
式中:k为波数;ω为弹性波频率,且k=ω/c。
从式(5)中可以看出位移近似解中包括频率为2ω的谐波成分,可以解释超声波与非线性源(接触面非线性应力-应变关系)相互作用导致的超声非线性效应,一般通过二阶超声非线性参量表征材料内部损伤,即
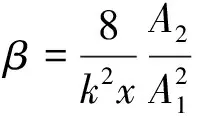
(6)
式中:A1为基波幅值;A2为二次谐波幅值;x为超声波的传播距离。
可以看出超声非线性系数是传播距离x的函数,和二次谐波幅值A2、基波幅值A1的平方有关,可以作为表征材料内部损伤的重要声学特征参数。
2 二维有限元仿真模型
2.1 微裂纹群非线性效应分析
以含微裂纹群的镁铝合金板(板长L为40 mm,板厚H为10 mm)为例,且已知镁铝合金密度ρ为1 770 kg·m-3,弹性模量E为46 GPa,泊松比ν为0.27。
在模型左侧施加水平方向均布的位移载荷,产生沿x轴正方向的纵波,激励信号为中心频率1 MHz的汉宁窗调制的5周期正弦信号,幅值AI=10 nm。镁铝合金板的模型如图1所示(图中l为模型增加附加长度),裂纹长度为2a,界面为硬接触,库伦摩擦系数μ=0.8。
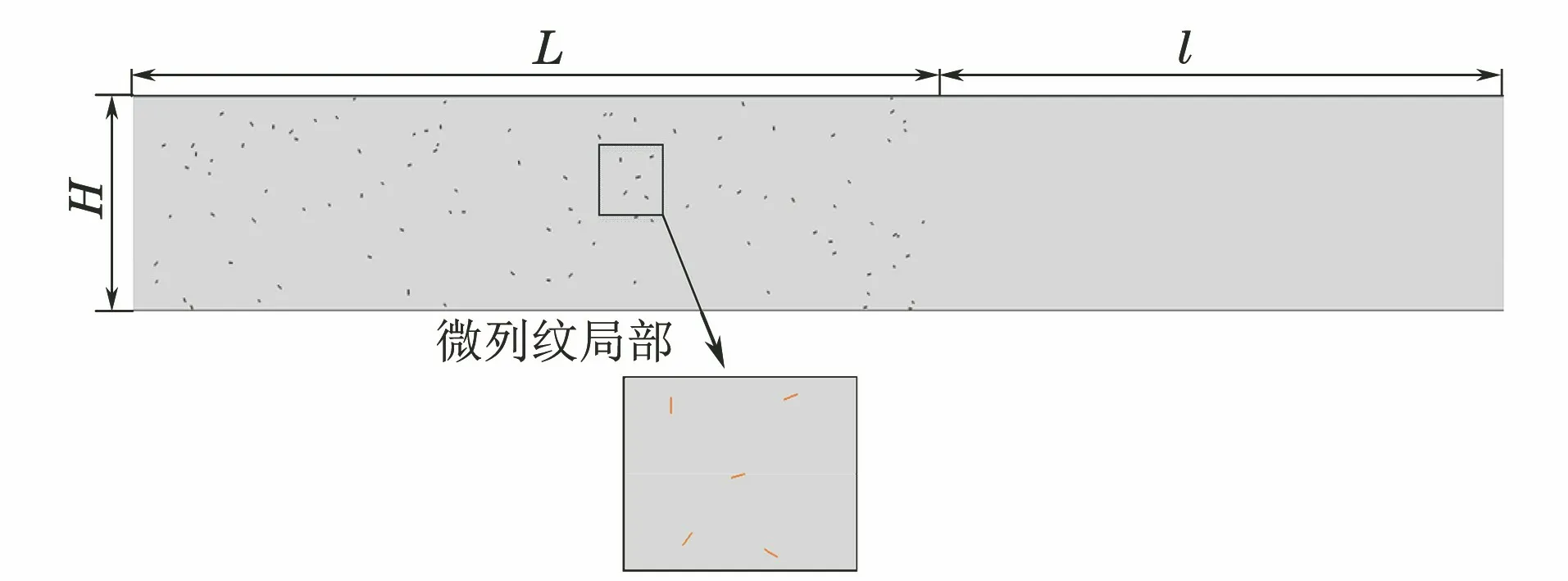
图1 含微裂纹群的矩形板
激励信号波形如图2所示,为了保证激励信号能完全通过微裂纹区域,且消除右侧边界反射对检测信号的影响,l应满足
l>10πc/ω
(7)
同时计算时间t满足
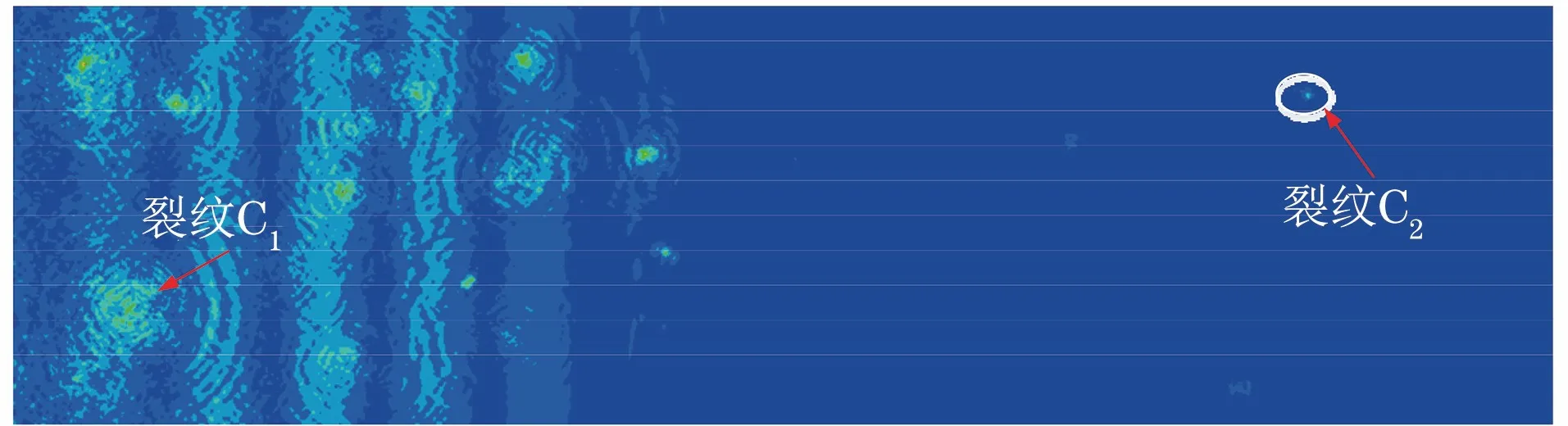
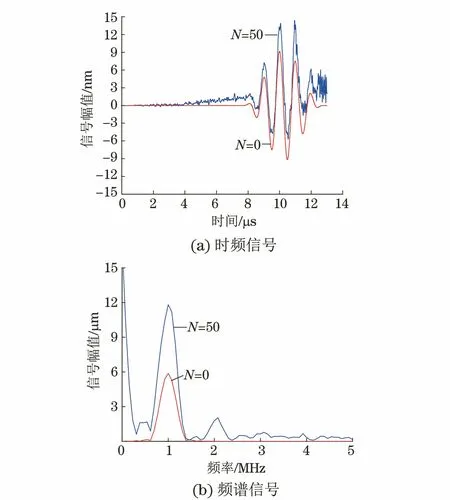
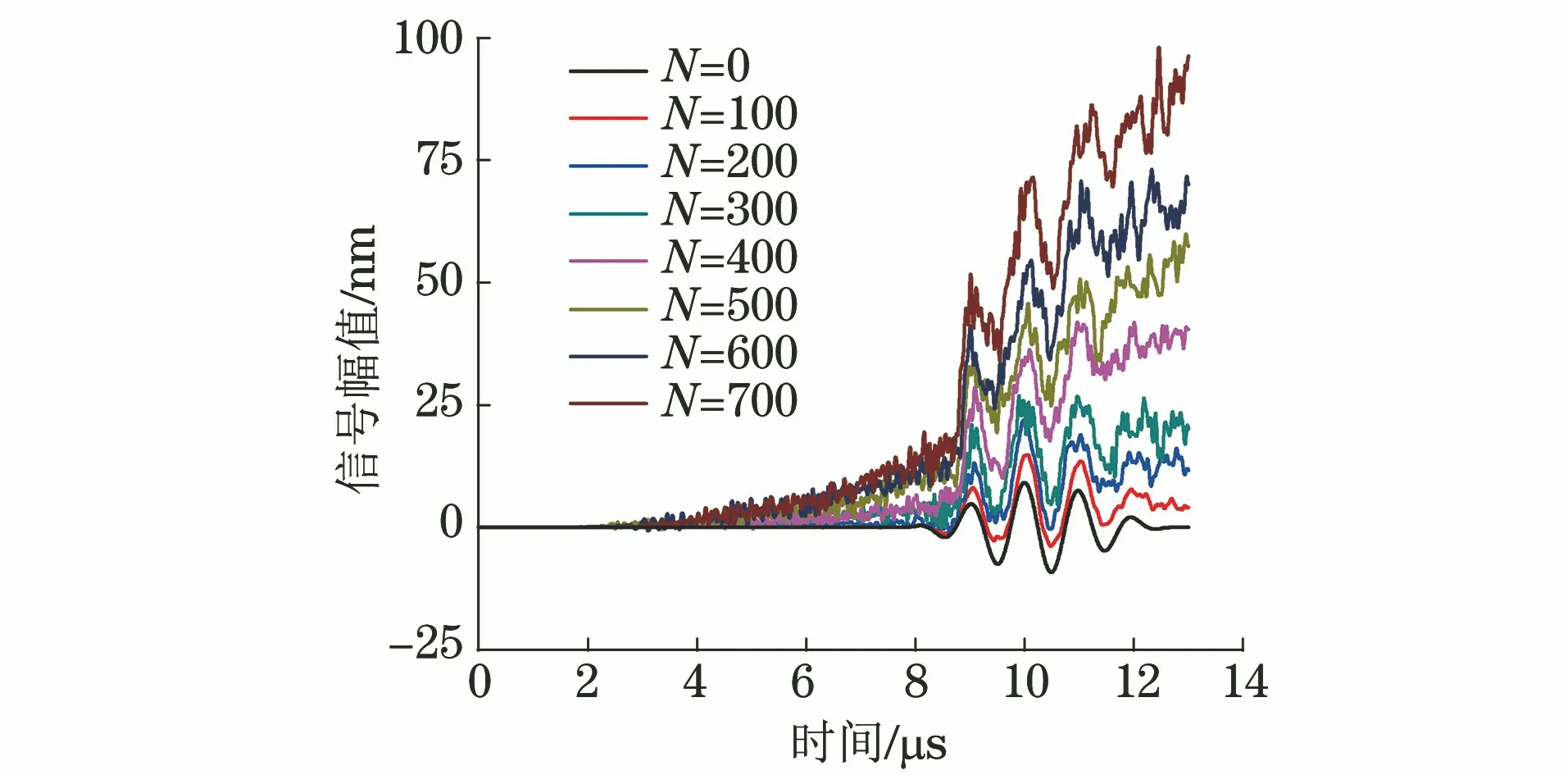
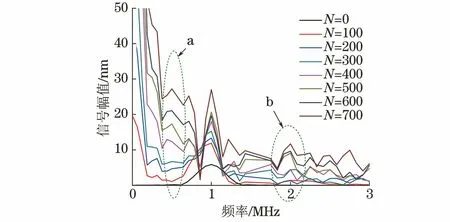
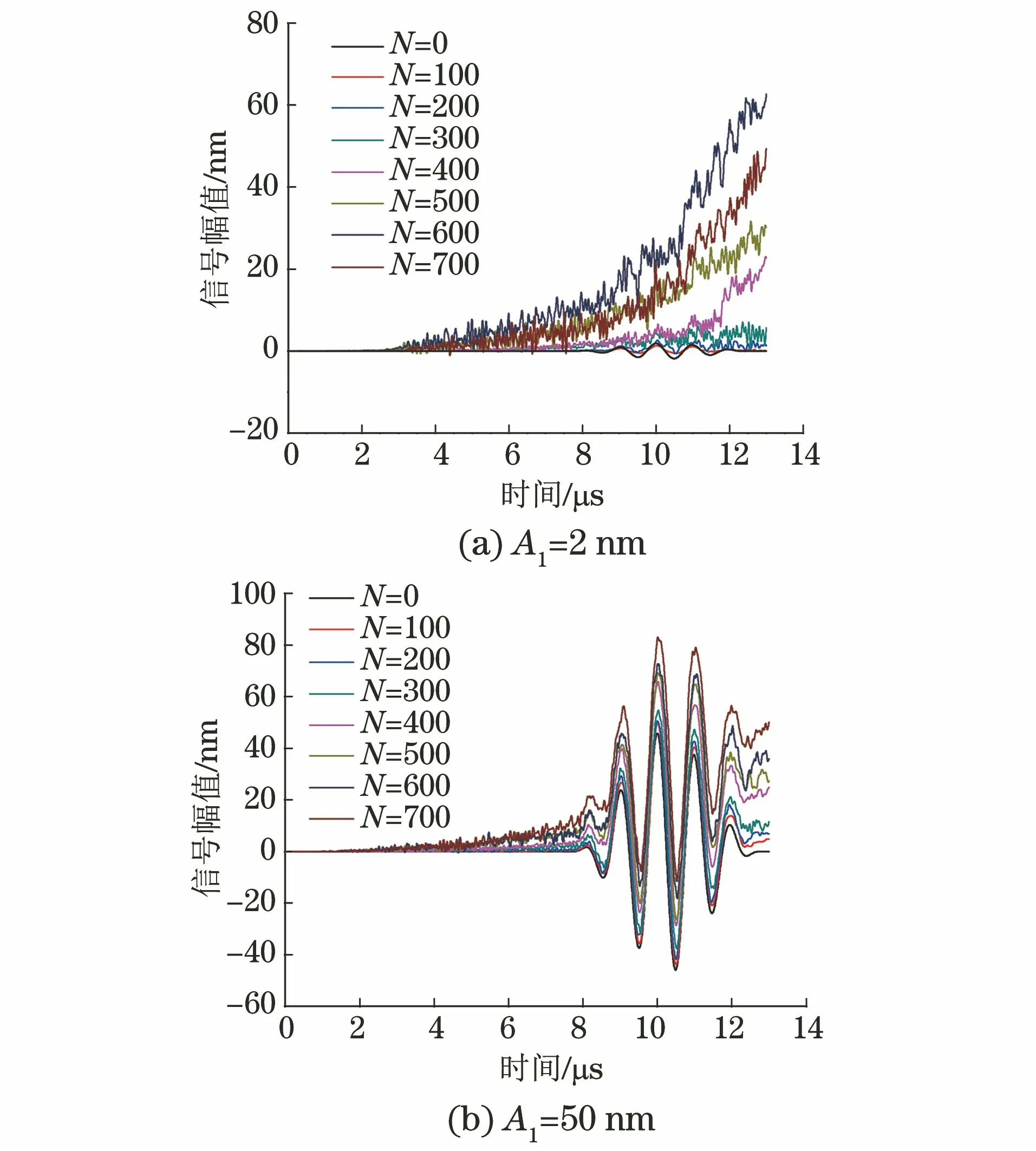
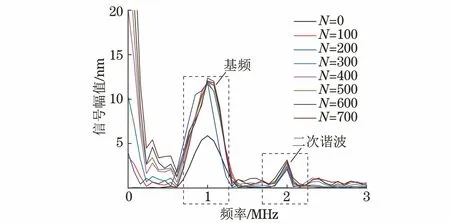
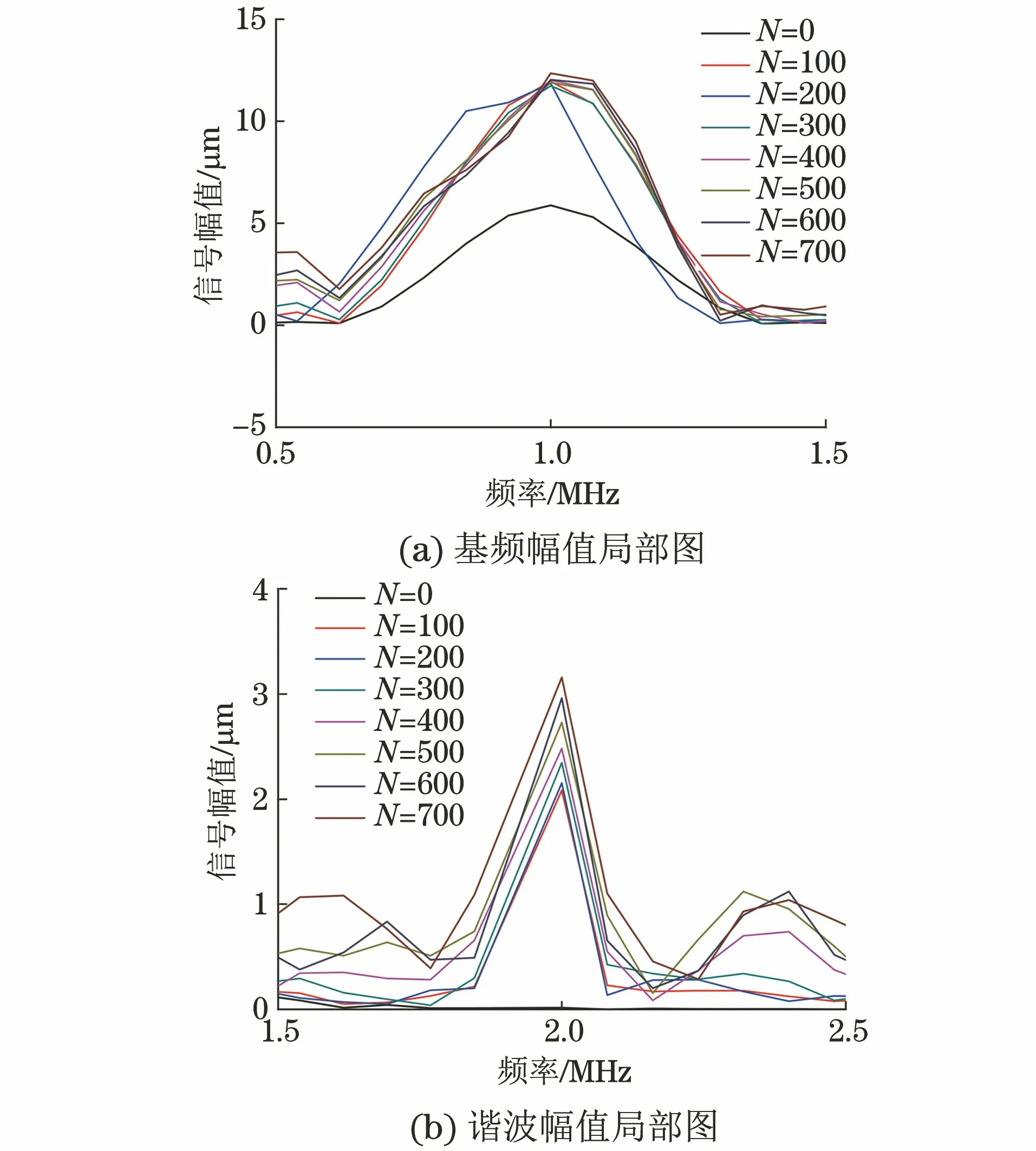
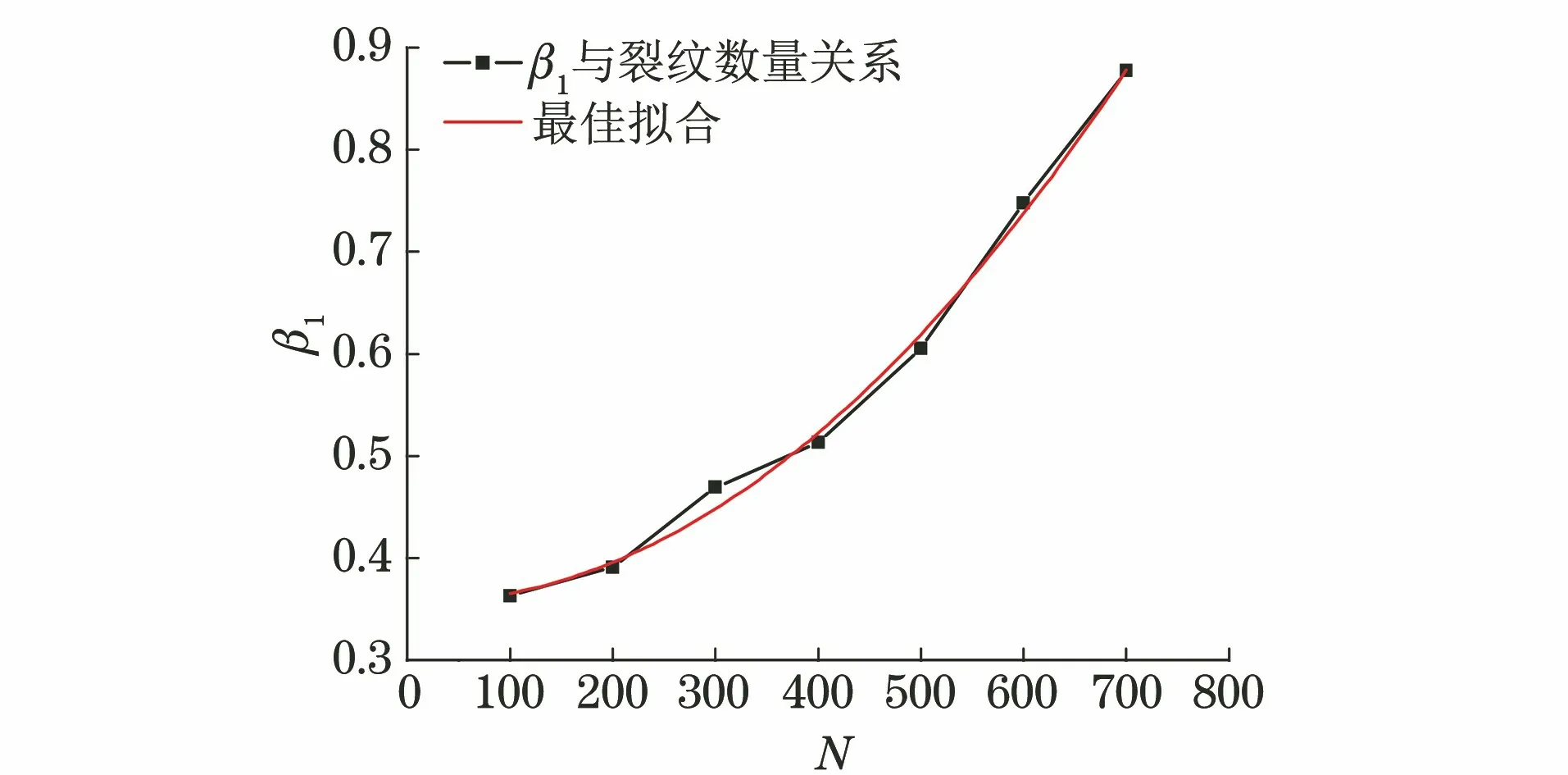
L/c (8) 图2 激励信号波形 为获得接触非线性效应产生的谐波分量,有限元模型网格尺寸需要满足条件 λmin/lmax≥10 (9) 式中:λmin为所关注的最小波长;lmax为网格最大尺寸。 模型采用ABAQUS/Explicit模块(显式动力学)求解,时间步长要满足Courtant-Friendrichs-Lewy稳定条件[17],即求解步长不能超出该稳定极限值 Δts≤lmin/c (10) 式中:lmin为最短单元尺寸。 入射波频率为1 MHz,二次谐波频率为2 MHz,根据式(9)和(10)选择最大网格尺寸和时间步长分别为0.2 mm和0.02 μs,并在裂纹附近局部细化网格。 选择微裂纹数量N=50的情况,微裂纹长度2a=0.1 mm,通过拉伸试验仿真分析模型力学性能。模型左侧施加F=1 kN·mm-1均布力,试验结果如下:裂纹数量N为0,50时,拉伸位移分别为9.929×10-2,9.967×1-2mm。结果显示此时裂纹几乎没有影响到材料的力学性能。 图3 含微裂纹群结构应力的云图(t=3.9 μs) 分别计算超声波在结构中的传播过程,以分析微裂纹群与超声波相互作用产生的非线性效应。图3为t=3.9 μs时刻含微裂纹群结构的应力云图,可以看出微裂纹长度小于超声波半波长,根据惠更斯原理,微裂纹成为衍射波二次声源[18],超声波通过微裂纹发生明显衍射效应,周围出现明显衍射波,如图中裂纹C1所示。 同时,超声波受微裂纹作用产生高次谐波,其传播速度大于基本波速,从图3中可以看出,该时刻激励信号没有传播到裂纹C2位置,而裂纹C2处已经出现了应力集中,该处的应力集中即为二次谐波作用导致。 为了进一步揭示微裂纹群与超声波非线性间的相互作用,选择(L,H/2)位置节点为传感节点,其水平方向位移时程曲线为检测信号,对两种情况下(N=0,50)的检测信号进行频谱分析和时频分析,结果如图4所示。 图4 微裂纹超声非线性特征分析 从图4(b)可以看出,微裂纹尚未影响到结构承载能力情况下,检测信号频谱特征已经表现出明显的超声非线性特征,即在频率f=2 MHz二倍频位置产生了二次谐波。除此之外,综合图4(a)可以看出,与单一裂纹(长度大于半波长)的超声非线性特征相比[12,15,19],微裂纹群超声非线性特征还有如下特点。 (1) 微裂纹群超声非线性特征更能体现传播距离的相关性。随着超声波的传播,微裂纹引起的二次声源逐渐增加,使得传感节点在较早时间点(约在时刻t=1.5 μs)就受到超声波的作用。在波形上表现为高次谐波,且波形逐渐偏离水平线,随着传播距离的增加,波形偏离逐渐明显。 (2) 超声波对微裂纹的衍射表现出与透射明显不同的传播特征。文献[12,15,19]中裂纹长度大于半波长,超声波透射通过微裂纹,检测信号谱峰发生明显衰减。文中算例超声波通过微裂纹的方式为衍射,能量损失较小,从图4(a)中可以看出检测信号谱峰值和谷值增加,幅值没有发生明显衰减。 (3) 超声波对微裂纹的衍射表现出与透射明显不同的非线性特征。由于透射导致的能量损伤,文献[12,15,19]中幅频曲线的基频幅值明显降低。由图4(b)的幅频曲线可以看出,微裂纹群导致多二次声源衍射波叠加,基频对应的谱峰出现明显增加,远高于无裂纹结构的谱峰。由于微裂纹接触面较小,二次谐波功率明显低于基频功率,三次及更高次谐波不明显。 微裂纹面开闭接触是产生接触非线性的主要来源,振动幅值是影响裂纹开闭的一个重要因素,当微裂纹数量增加时,二次衍射波叠加将影响裂纹的开闭状态,选择裂纹N=100700(步进100)时的情况进行仿真,为得到更具一般性的结果,每种算例计算50次,取计算结果的均值以消除随机性影响。计算结果如图5所示,其频谱图如图6所示。 图5 不同数量微裂纹群的超声检测信号(AI=10 nm) 图6 不同数量微裂纹群的检测信号频谱图(AI=10 nm) 由图6可以看出,随着裂纹数量增加,二次谐波叠加产生更为复杂的频率成分,在接近1/2分频位置(图中a处位置)对应的谱峰明显增加,当裂纹数量N=700时,该处谱峰与基频(频率f=1 MHz)处谱峰接近;在基频位置,谱峰明显,且幅值随着微裂纹数量增加而增加;同时,在2倍频(图中b处位置)区域,虽然幅值随着裂纹数量增加而增加,但是谱峰并不明显。 结合检测信号波形和频谱分析结果可以看出,随着裂纹数量的增加,二次谐波的叠加不仅影响超声波的传播特征,还进一步影响裂纹开闭而产生更为复杂的频率成分,裂纹数量较多时,衍射效应会严重影响超声非线性特征,进而影响缺陷检测精度。 从上一节的分析可知,随着裂纹数量的增加,二次谐波叠加将导致检测信号偏离和畸变,且产生更为复杂的频率成分。下面将讨论激励信号幅值改变时,二次谐波变化情况。采用同样的模型,分别选择激励信号幅值AI为2,50 nm时的情况进行超声非线性分析,得到的结果如图7所示。 图7 不同激励幅值时的超声检测信号 图8 不同微裂纹群检测信号频谱图(AI=50 nm) 图9 检测信号的基频和二次谐波频谱图 由计算结果可以看出,当激励幅值较低时(AI=2 nm),检测信号受衍射作用更为强烈,与图5相比,波形畸变和偏离程度都更加明显,裂纹数量N=400时,检测信号已经看不出激励信号波形特征;激励幅值较高时(AI=50 nm),检测信号受衍射作用较为轻微,裂纹数量N=700时,检测信号仍具有明显的激励信号波形特征。即,检测信号波形畸变情况和偏离程度可以作为超声非线性效应的重要参考。进一步对图7(b)进行傅里叶变换,得到频谱图如图8所示。 由图8所示的检测信号频谱分析结果可以看出:裂纹数量增加,基频幅值几乎没有变化[见图9(a)],二次谐波幅值随着裂纹数量的增加而增大[见图9(b)]。取相对非线性系数 (11) 计算相对非线性系数β1与微裂纹数量的关系,并进行拟合,得到的关系曲线如图10所示。 图10 相对非线性系数与微裂纹数量的关系曲线 随着裂纹数量的增加,相对非线性系数呈二次函数关系增加,最佳拟合函数如式(12)所示。 β1=0.357 2-2.77×10-5N+1.1×10-6N2 (12) 针对材料早期损伤检测问题,基于随机分布微裂纹群建立有限元模型,求解了超声非线性特征,主要结论如下。 (1) 超声非线性技术对早期微裂纹群检测具有很高的灵敏度,损伤几乎未影响到材料性能的情况下,检测信号已经表现出非常明显的非线性特征。 (2) 微裂纹长度小于半波长时,超声波通过微裂纹的方式为衍射,能量损失较低,检测信号幅值没有明显衰减,检测信号出现畸变以及逐渐偏离水平位置,这些现象可以作为产生超声非线性特征的重要参考。 (3) 由于微裂纹群的衍射作用,超声非线性特征不仅与微裂纹数量有关,也受激励信号幅值的影响较大。激励幅值较小时,随着微裂纹数量增加,产生更为复杂频率成分,1/2分频位置幅值增加,且2倍频位置幅值不明显,将影响检测结果。 超声非线性技术在微裂纹群检测方面具有广泛应用前景,由于微裂纹群与超声波相互作用较为复杂,还需要进一步研究激励幅值-裂纹数量-二次谐波激发效率间的定量关系,为材料劣化性能评估做支撑。
2.2 微裂纹检测能力灵敏度分析
3 微裂纹群超声非线性特征分析
3.1 衍射对超声非线性特征影响
3.2 激励幅值对超声非线性特征影响
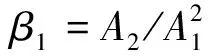
4 结果与讨论
