轴承润滑油膜厚度测量理论及仿真研究
2020-04-22陈继明马希直李响
陈继明,马希直,李响
(南京航空航天大学 机电学院,江苏 南京 210016)
0 引言
在工业机械中,为了减少磨损,增加机械的使用寿命,通常使用液体油液润滑,轴承油膜厚度一般为0.1~100μm[1-2]。早期,许多学者使用电学法来测量润滑油膜的厚度,但此种方法必须要先测量电容与电阻抗,还需安装传感器等,且测量的精度达不到要求。而超声波测量具穿透能力强,精度高等优点,受到国内外学者的青睐。目前,更多的研究人员投入到超声波的理论和声反射系数理论的研究中来,并随着有限元软件的不断更新,使得声学的仿真也变得更加方便。本文通过建立轴承结构的简化模型,分别进行理论计算和仿真模拟,得到声反射系数随频率的变化规律,并对比二者结果具有较好的一致性。
1 理论计算
高速运转机械中,为保证机械正常运转并延长使用寿命,液体润滑油膜起到至关重要的作用。如图1所示,建立了I不锈钢、II油域、III不锈钢三层结构,其中两层不锈钢模拟无限大区域。

图1 三层介质模型
由超声波相关的反射与透射理论可知,超声波在第一层交界面的反射系数与材料的密度、声速、油域厚度、不锈钢声阻抗有关。在轴承润滑系统中,油膜厚度变化范围在0.1~100μm之间,本文讨论30~100μm厚度油膜的情况。
当中间层油膜厚度较厚,即30~100μm厚度时,油膜的质量不能被忽视,多使用共振模型去测量润滑油膜厚度。国内外许多研究人员(HOSTEN[3]、 KINRA[4]、 PIALUCHA & CAWLEY[5])在利用超声波反射系数法测量油膜厚度方面作了许多研究。研究认为不锈钢、油膜、不锈钢三层结构中边界的应力应变是连续的,可以利用共振模型来进行声反射系数的理论计算。图2为声波在三层结构中的传播示意图,Ti和Ri分别表示入射波和反射波振幅。
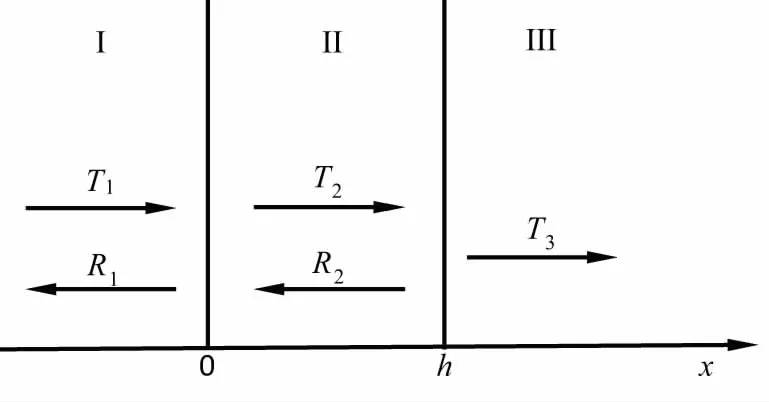
图2 三层介质中声波传播模型
给定入射声波幅值T1为1Pa,超声波垂直入射,根据位移-应力关系,结合界面处位移和应力连续的声学边界条件,可推导出反射系数R的表达式[6]:
(1)
式中:zi为结构的声阻抗,g=eiωrh/c1,c1为油域中的超声波声速。
由声学相关理论得知,当油膜厚度为半波长的整数倍时,油膜发生共振,共振角频率ωr为[7]:
ωr=πc1m/h
(2)
经过变形得油域厚度为:
(3)
式中:m为整数,表示谐振阶数;fm为m阶共振频率。
当入射波频率等于油膜共振频率时,g2=1,联合式(1),可得:
(4)
由式(4)可知,当油膜两侧介质相同时,反射系数为0,因此在实际测量中,可通过提取反射系数极小值处对应的共振频率并结合式(3)求出油膜厚度。
2 有限元法分析反射系数
目前许多研究人员对反射系数作了研究,而且由于有限元仿真软件和工作站硬件的不断更新,基于声反射系数的声学仿真也变得更加方便。本节对共振模型厚度的润滑油膜进行仿真研究,在后处理中利用声功率求出反射系数。
2.1 声学控制方程
描述流体中声音传播的控制方程包括:用连续性方程描述的质量守恒方程、运动方程以及描述热力学变量的物态方程;在经典压力声学中,控制方程对于绝大部分声学现象都能精确描述[8]。
假设流体无损耗且绝热,忽略黏性效应,并使用线性等熵状态方程。声场以一个变量声压p描述,可以得到流体波动方程为:
(5)
式中:t表示时间;c0为声速(绝热的)。
平面波入射时,入射压力pi为:
pi=p0e-i(k·x)
(6)
式中:p0为入射压力幅值,波沿着矢量k方向以角频率和波数k=|k|行进。
声-固耦合表现为两相介质之间的相互作用,固体在声压作用下会产生变形或运动,变形或运动又反过来影响声压场。在声-固耦合边界处,通过声压和弹性体质点加速度的相互转换进行描述,其边界控制方程为:
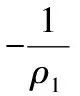
(7)
FA=pt
(8)
式中:an为垂直加速度;pt为总声压;ρ1为固体密度;FA为固体域边界载荷。
2.2 反射系数的计算
反射系数可用声功率来计算,入射声功率Win和透射声功率Wout可通过对界面压力进行积分求得,其表达式如下:
(9)
(10)
式中:p0为平面波入射压力值;|pc|为绝对压力值;ρ、c为介质密度和声速。
因此,声反射系数可通过下式求得:
R=(Win-Wout)/Win
(11)
2.3 建立有限元模型
根据图3(a)所示的轴承结构简化图,为了避免仿真过程中声波多次反射影响结果,在有限元分析软件comsol中建立相应的最终简化分析模型如图3(b)所示。三层结构分别为不锈钢、油液、不锈钢。第一层不锈钢上边界设置为平面波辐射-入射压力场,大小为1Pa。用模拟超声换能器产生超声波,超声波在不锈钢与油液域交界面发生反射和透射,轴颈下半部分设置为平面波辐射,以模拟无限大的声场区域。
对于此次模拟的共振模型,油膜厚度应为10~200μm。采用压力声学物理场,并设置油膜厚度为30μm、50μm、70μm、90μm和110μm,网格最大尺寸为声波长的1/10。采用频域分析,频域范围为0~30MHz,扫频间隔为0.01MHz。
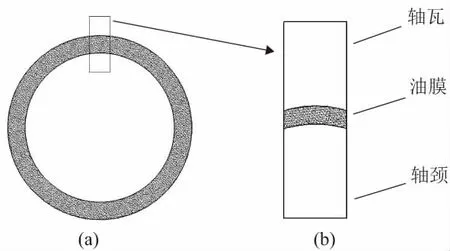
图3 模型
2.4 结果分析
1) 声压分析
不同油膜厚度在共振频率下的声压分布如图4所示。由图4可以看出曲面油膜处于共振频率时,声压幅值在0.8~1.2Pa之间,说明共振时的反射字数在0.2以内,即此时声压几乎全部透射。
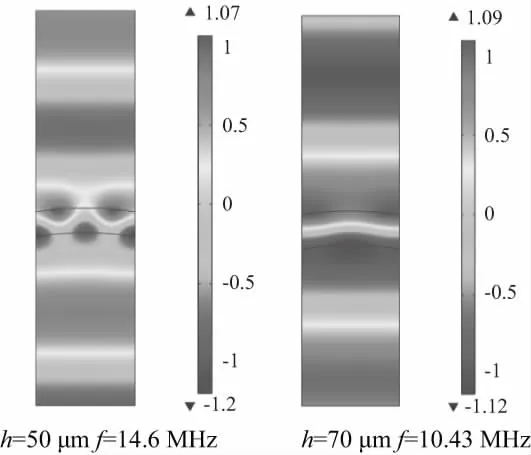
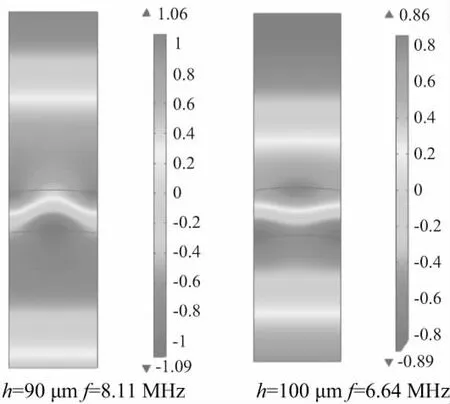
图4 不同油膜厚度在共振频率下的声压分布
当频率不在相应油膜共振频率附近时,声波大部分发生反射,此时反射系数接近于1。当油膜厚度为30μm,频率分别为20MHz和24.33MHz(共振频率)的声压场分布图如图5所示,。当f=20MHz时,声压大部分发生反射,下不锈钢域中的声压值很小,即只有少部分发生了透射,上不锈钢域中声压幅值最大为0.2Pa,这是声波发生了反射并且和原来声波发生了叠加导致,说明反射系数在0.8以上;而当f=24.33MHz,即达到共振频率时,声压大部分发生透射,反射系数在0.2以内。

图5 30 μm油膜厚度的声压场分布
2) 反射系数分析
在后处理中利用声功率理论计算出共振模型下不同油膜厚度的反射系数,如图6(a)所示。油膜的第一阶共振频率随着油膜厚度的增加而减小,在油膜的相应共振频率处,反射系数接近0,即此时声波全部发生透射,而远离共振频率时,反射系数接近1,即此时声波全部发生反射。图6(b)是理论计算的反射系数随频率变化的曲线。对比图6(a),有限元计算的结果与理论计算结果具有较好的一致性。但二者还是有略微的不同,有限元分析的反射系数在共振频率点与0还有一定的差距,而理论分析的结果则更接近于0。两图都能明显地识别出共振点,并且共振频率高度一致,后期可以由共振频率直接求得油膜厚度。有限元仿真时,各个反射界面并不是理想的反射界面,所以有一定的误差。
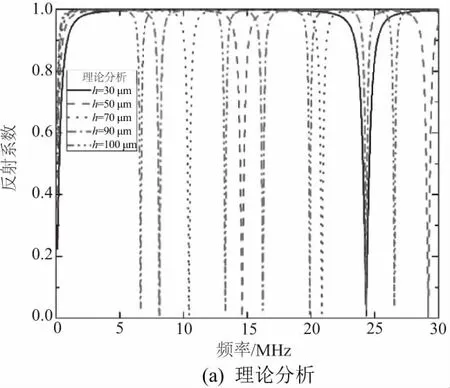
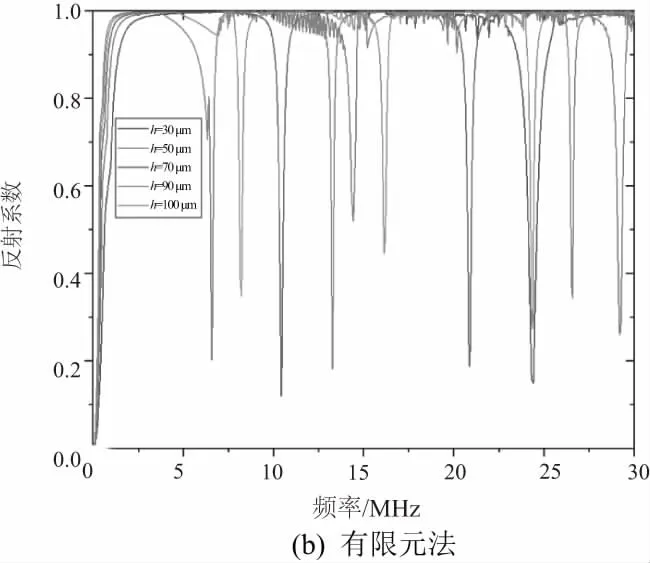
图6 反射系数曲线
3 结语
利用有限元法对声反射系数进行了计算,直观地查看了平面波反射和透射的声压场分布,并利用声学理论结合软件后处理计算了反射系数曲线,与理论结果进行对比,两者有着较好的一致性,说明了应用有限元法进行油膜反射系数计算的准确性。
