阶梯轴类零件激光在机测量误差补偿研究

尉渊，丁大伟，赵正彩，刘英智，徐九华

(1. 北京星航机电装备有限公司，北京 100074； 2. 南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

在机测量(on-machine measurement, OMM)技术实质是指在前后工序间隙对零件实际形状尺寸进行现场快速测量，及时发现加工偏差，以便在加工中实时进行误差补偿，进而提高加工精度与效率。激光在机测量是非接触式动态扫描过程，效率较高，测量精度主要受机床误差、传感器误差及安装误差等影响。因此，为提高激光在机测量精度，国内外学者从测量原理、机床精度、路径规划、模型重构及误差分析等方面进行了深入研究。对阶梯轴类零件在机测量而言，卡盘跳动与尾架偏差无疑会对结果产生较大影响。国内外许多学者对车床主轴回转精度检测进行研究，郑相周等[1]设计的计算机测量系统识别了径向跳动、端面跳动和角度摆动误差，并可在计算机上用3D图形表达。SHOJI等[2]提出矢量表示方法，用垂直于轴线的矢量来计算主轴径向回转误差；ROBERT等[3]改进反向法，通过设计转台减少位移传感器的移动和调整，从三维角度显示主轴径向和轴向同步误差。

此外，合理规划测量路径可快速而准确获取测点位置坐标，DING等[4]基于CAD模型提出三维激光扫描路径规划方案；王禹等[5]构造1×30×1的BP神经网络模型，很好地提高了路径拟合和预测的准确性及效率。后期需对采集数据进行处理时，高瑞等[6]提出一种复杂曲面零件散乱点云特征点提取方法，直接操作于散乱点云；沈琰辉等[7]提出一种新的基于邻域离散度的异常点检测算法，性能稳定。后期对数据进行光顺处理[8]，便于模型重构及误差分析。

基于上述思路，诸多激光在机测量系统应运而生，如：KLAUS等[9]提出1D-3D物体(5m×5m×5m)测量概念，采用激光跟踪仪构建完整M3D3在线测量系统，可实现对大尺寸工件的精确测量。NISHIKAWA等[10]选用性能良好的激光位移传感器代替探针，将截面测量结果与CAD模型及三坐标测量数据对比分析发现误差相对较小。YANG等[11]为提高测量精度，采用激光干涉仪提出一种干涉图拼接法来测量曲面形状偏差，并验证了该IFP拼接算法的有效性。

本文基于SK50P型三轴数控车床，在刀架上通过辅助工装搭载激光位移传感器，对阶梯轴类特征零件进行在机测量。首先制作两端呈锥度的高精度标准件，用于车床实时误差表征，并设计误差补偿算法，计算不同角度下补偿值；然后处理数据并重构模型，分析误差补偿前后激光在机测量精度，验证补偿效果；再由传感器与台阶特征位置几何关系计算出点云偏转角度，对初始测量点云进行修正，并与三坐标测量结果进行对比，分析测量误差，实现阶梯轴类零件高精度激光在机测量。

1 试验及方法

1.1 试验装置

激光在机测量装置的基本结构如图1所示。该系统以数控车床为运动载体，以LK-G80型点扫描激光位移传感器为轮廓信息采集装置，搭配LK-Navigator软件实现对阶梯轴型面的自动化扫描及数据导出、存储等，并用于误差补偿与分析。

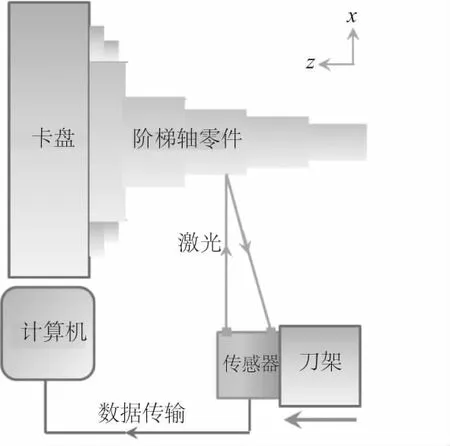
图1 测量装置示意图

1.2 试验方法

首先，建立测量坐标系，选择传感器进给速度F=120mm/min。由于刀架启动并达到进给速度需要一定时间，因此在编程时预留响应距离，使得传感器能稳定可靠地进行阶梯轴型面数据的采集。测量中利用卡盘上的分度将阶梯轴每次旋转30°，然后运行测量程序进行数据采集，共测量12组数据。阶梯轴理论模型及测量路径规划如图2(a)所示。

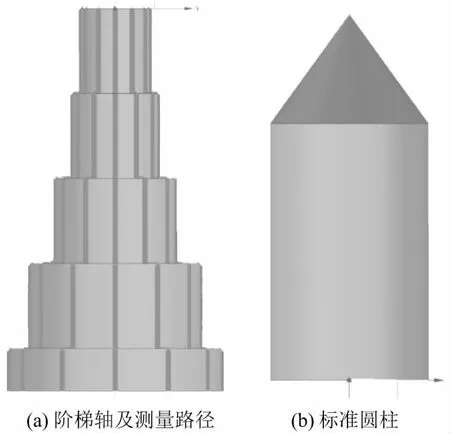
图2 阶梯轴和标准圆柱理论模型

在工件与尾架顶针间装配标准圆柱，其模型如图2(b)所示。圆柱两端分别与工件及顶针锥度连接，并且是线接触，可移动。通过数据处理将尾架偏差剔除，对不同角度下的卡盘跳动进行评价，并将该误差补偿进型面测量结果，实现高精度激光在机测量。

2 误差补偿算法

激光在机测量过程中，主轴跳动与尾架偏差的影响最大，且该类偏差不稳定，需实时检测，因此在阶梯轴与尾架间装夹标准件来表征误差。该标准件由高精密外圆磨工艺制成，圆度可达0.0005mm，两端分别有60°锥孔和锥尖，装夹过程中尽量保证阶梯轴、标准件、尾架顶针在同一高度上。随后对标准件表面测量数据进行最小二乘线性拟合，如图3所示。

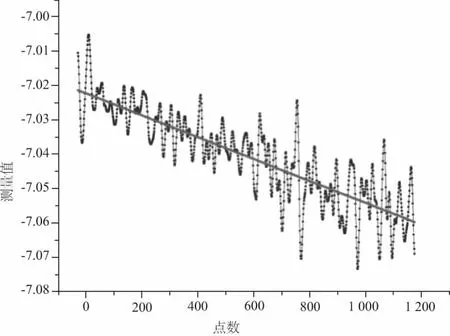
图3 最小二乘线性拟合

由图3可知，标准件圆柱面测点数据不规则，其总体趋势呈单调下降。为此，线性拟合后，计算两端点数据差，即为主轴跳动与尾架偏差之和，设为αi，则

αi=βi+γ(i∈[1,12] ,i∈N)

其中：αi为端点数据差；βi为主轴跳动误差；γ为主轴中心线与尾架偏差；N是自然数，表明i取整。

为确定不同角度测量数据的补偿值，以其中某一角度的偏差值为基准，设为α0；计算其他角度相对偏差值，得：

αi-α0=(βi+γ)-(β0+γ)=βi-β0

取阶梯轴各圆柱面测量值的平均值，为Lim(m=1,2,3,4,5)，基准角度测量值为L0m，因此，测量数据平均值之差为：

k∈[0,11] ,m,k∈N)

建立δi-(αi-α0)的线性关系，可由MATLAB线性拟合得到，程序如下：

p=polyfit(αi-α0,δi,1)

经计算，拟合得关系式：

δi=-0.674×(αi-α0)-0.0027

随后，代入不同αi-α0，计算相应的δi，作为其补偿值，结果如图4所示。

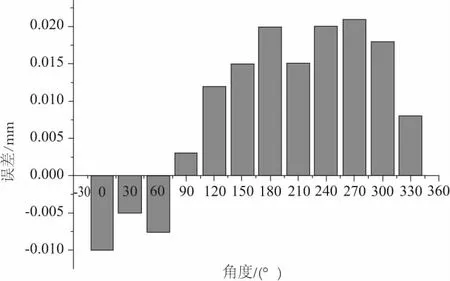
图4 不同角度下误差补偿值

3 结果与讨论

3.1 误差分析

首先进行误差补偿，并将坐标点云导入UG中并重构模型，通过“面到面”检查来分析其误差，结果如图5所示。

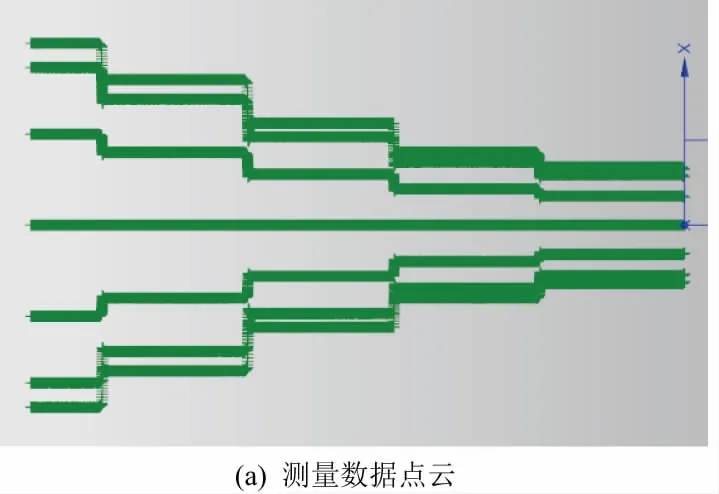
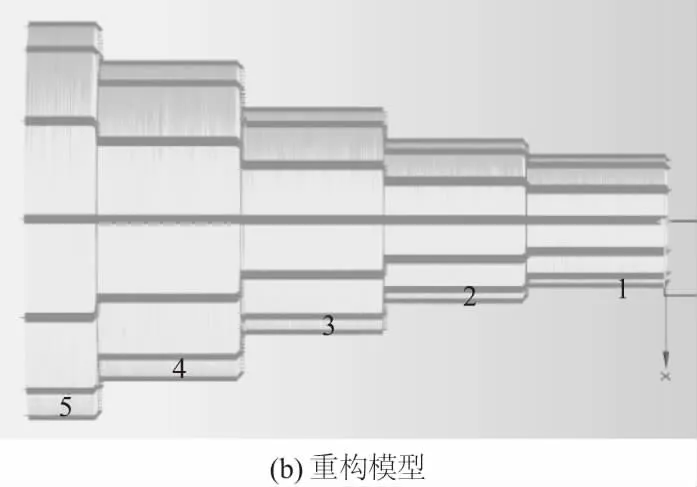
图5 数据点云及模型重构

为分析其误差，由图5(a)中的测量数据点云重构出图5(b)中的零件模型，并将其与三坐标测量结果对比分析。将模型各圆柱面沿z负向编号，分别为1、2、3、4、5，如图5(b)所示；调用“面-面”偏差指令来评价其补偿前后分别与三坐标修正模型间误差，如图6所示。

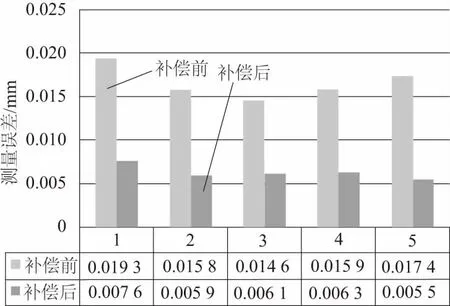
图6 补偿前后测量误差

由图6可知，在误差补偿前，测量重构精度在0.0146mm～0.0193mm之间，而经误差识别补偿后，精度可达0.0055mm～0.0076mm，可有效提高激光在机测量精度。

3.2 台阶面精确测量

复杂曲面零件常包含台阶等特征，如何对台阶面信息进行准确表达是个关键问题。主要原因有：接触式测头虽能满足大部分高精度测量要求，但由于测头半径的存在导致台阶面爬升起点和终点尖锐处难以测量，如图7(a)所示；而非接触式测头，如激光传感器等，则可能存在光线被遮挡等现象使得测量数据缺失，如图7(b)所示。

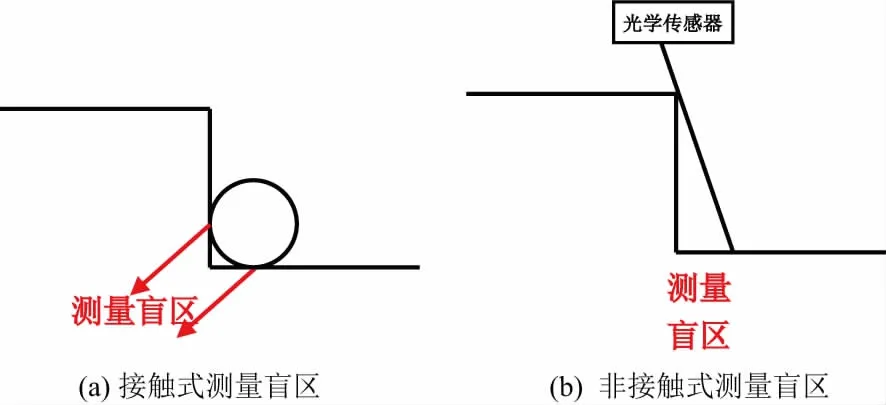
图7 台阶面测量盲区

为此，为完整获取台阶处特征信息，参考激光传感器斜射测量方式，将激光测头逆向偏转12.5°，使发射光束与接收光束之间夹角为25°。微调并运行测量程序，测量数据如图8所示。

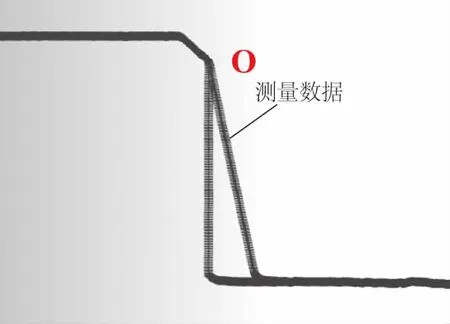
图8 测量点云

该特征与真实台阶之间也存在一个旋转角度，设为α，其关系如图9所示。

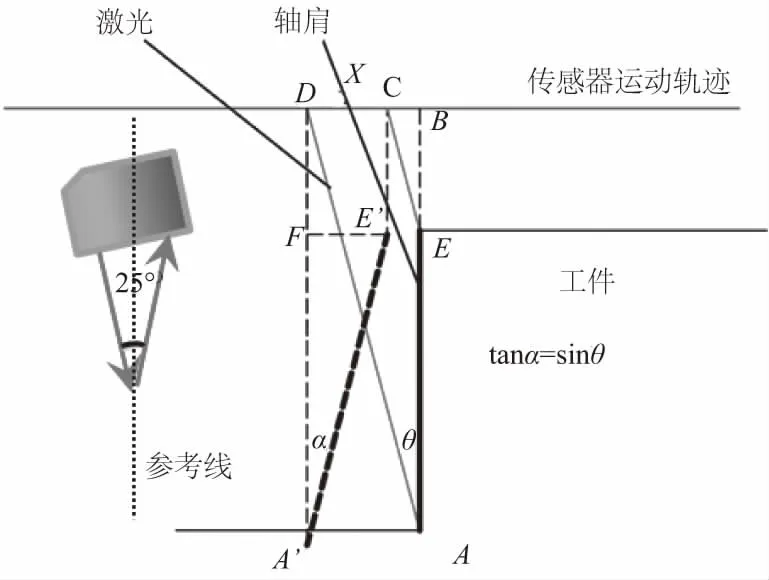
图9 拟合特征与真实台阶数学关系

已知：AD、CE'为红外光线长。其中A'E'为测量拟合值。

在△A'E'F中，

E'F=CD

A'F·tanα=A'F·sinθ

tanα=sinθ

由此可得α=12.213°，旋转后如图中箭头所示。台阶高度为6mm，因此平面度为：T=6×sin0.112=0.011mm，这与三坐标测量台阶平面度0.009mm非常接近，意味着台阶处数据拟合精度高。

4 结语

1) 设计并制作标准圆柱用于误差表征，提出误差补偿算法；通过测量及拟合，给出不同角度下误差补偿值在-0.01mm～0.021mm之间，该值主要是卡盘跳动误差及尾架偏差。

2) 误差补偿前后分别对测量点云进行模型重构，结果表明，补偿前测量偏差在0.0146mm～0.0193mm之间，补偿后精度可达0.0055mm～0.0076mm。

3) 激光测量台阶平面度为0.011mm，与三坐标测量机所测0.009mm相近，表明该测量方法可行。