基于流固耦合的航行体高速入水规律研究

魏洪亮，赵 静，徐志程，俞启东，李 明

基于流固耦合的航行体高速入水规律研究

魏洪亮，赵 静，徐志程，俞启东，李 明

（中国运载火箭技术研究院研究发展中心，北京，100076）

针对航行体高速入水过程中的流固耦合问题，采用有限元软件LS-DYNA中基于任意拉格朗日-欧拉（Arbitrary Lagrange-Euler，ALE）的流固耦合方法，首先对美国MK25鱼雷模型的入水过程进行动态模拟，获取模型入水过程中的冲击效应和随时间变化的过载，得到不同时刻的流固耦合形态，验证了仿真方法的有效性。然后针对某航行体模型的质量、缩比效应、速度、入水角度等因素进行了仿真研究，结果表明决定高速入水过载的最重要因素是入水速度，入水角度对过载的影响相对较小，分析缩比结果验证了缩比定律的有效性。

任意拉格朗日-欧拉；流固耦合；跨介质；高速入水

0 引 言

在空投鱼雷的入水、两栖飞机的水上降落等过程中，结构会激起周围流体的运动，同时流体对结构也施加反作用力，属于典型的流固耦合现象。入水是一个短暂、变化剧烈而又复杂的力学过程，特别是在入水冲击瞬间通常会形成很大的冲击载荷[1]。结构入水冲击过程中形成的轴向力作用可能导致航行体头部变形、仪器设备失效等；法向力作用会影响弹道，并可能使结构弯曲破坏[2]。因此，研究结构入水冲击问题具有重要的工程意义。对于具有复杂边界条件的流固耦合问题，可以采用有限元软件LS-DYNA中的任意拉格朗日-欧拉（Arbitrary Lagrange-Euler，ALE）方法进行求解。ALE方法处理物体入水冲击问题具有较大的优越性，它几乎不受几何外形、边界条件以及载荷情况的限制，可以对物体、空气和水进行非定常耦合计算，可以克服许多解析方法无法解决的困难，如入水引起的液面变化、结构的变形及入水的空气影响等。潘光[2]等采用LS-DYNA对空投鱼雷的入水载荷问题进行了仿真研究，孙琦[3]等对鱼雷弹体撞水过程进行了流固耦合动力分析，张虚怀[4]采用LS-DYNA对飞船返回舱的着水冲击问题进行了模拟。

本文采用LS-DYNA软件，以ALE方法来描述流体单元，并通过以罚函数为基础的耦合算法，与拉格朗日方法描述的结构进行流固耦合计算，来模拟某航行体高速入水过程，研究高速入水规律。

1 基于ALE的流固耦合方法

1.1 基本控制方程

基于ALE算法的质量守恒方程和动量守恒方程为

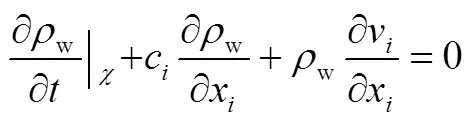
1.2 流体材料模型

在LS-DYNA软件中，对空气和水的性能模拟均采用空材料（*mat_null）模型描述粘性应力的本构关系，采用状态方程描述主应力的本构关系。水的模型采用Gruneisen状态方程[5]：

空气模型采用线性多项式状态方程，其压力计算公式为

1.3 耦合计算方法

LS-DYNA程序采用交替求解法求解流固耦合问题[6]。交替求解方法是将流体和结构分成两个单独的求解域，在数值求解过程各时刻交替求解这两个区域，并通过耦合界面进行有关物理量的传递。耦合界面上的结点速度传递给流体，作为流体区域的速度边界条件，利用ALE方法单独求解流体域；耦合界面上的结点力传递给结构，作为固体域的力边界条件，按传统方法单独求解动力学方程。当流体域和固体域同时达到精度要求时结束迭代，根据耦合界面的运动情况更新单元网格进入下一时间步的求解。

2 仿真方法验证

2.1 仿真模型

采用有限元软件LS-DYNA中基于ALE的流固耦合方法，首先对美国MK25鱼雷模型的入水过程进行模拟，验证仿真模型和仿真方法的有效性。MK25鱼雷模型为70°半球角的橄榄形头型，不考虑其变形，设为刚体，采用壳单元，共分为6751个单元， 6665个结点。空气和水材料间设置为共结点，上层为空气介质，采用实体单元，分为115 200个单元， 124 257个结点；下层为水介质，采用实体单元，分为230 400个单元，242 597个结点；整个模型共包括 352 351个单元，367 602个结点。MK25鱼雷模型入水仿真有限元网格如图1所示。

图1 MK25鱼雷模型入水仿真有限元网格

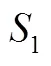
2.2 计算结果分析

图2分别为MK25鱼雷模型在3 ms、6 ms、9 ms、12 ms不同时刻的入水状态。由图2可知，模型入水后迅速与液体发生作用，形成侵入干扰区，该区域中充满空气，形成上下非对称的空泡形态，同时液体表面发生显著变化，部分液体因获得速度而被激起，形成水面浪花。随着结构不断入水，空泡区域逐渐增大。除头部与水介质接触外，模型尾部的部分区域也与水介质发生接触，形成部分沾湿区。图3为模型入水过程中加速度随时间变化曲线，由图3可知，模型触水（约2 ms）时刻加速度曲线出现阶跃，形成入水冲击效应，然后加速度曲线缓慢减小，在约9 ms时刻，加速度曲线出现一个尖峰值，是模型尾部与水接触所致。

图3 加速度随时间变化曲线

通过对图3中的时域加速度曲线进行快速傅里叶变换（Fast Fourier Transform，FFT），可以得到模型在入水过程中的静态过载值为38.8。文献[7]中针对本文中的缩比模型开展入水试验研究，并根据试验数据拟合得到不同头型的过载计算公式，对于本文中70°半球角的橄榄形头型，通过计算可以得到其过载试验值为30.4。因此，本文仿真结果误差为27.6%。可见，针对瞬态、非定常、复杂的流固耦合问题，基于ALE的方法能够再现模型入水过程的特点，过载结果的预示精度较高，可以通过仿真手段定性获取航行体跨介质入水过程的规律特性。

3 航行体入水规律研究

采用LS-DYNA 软件对航行体模型开展入水过程流固耦合建模和仿真。航行体、空气和水的材料性能参数与2.1节中设置的相同，航行体模型为尖锥头型，不考虑其变形，设为刚体，采用壳单元，通过设置单元壁厚来调整模型质量，其中航行体共分为8701个单元，8689个结点；空气与水共结点，空气分为 115 200个单元，124 257个结点；水分为230 400个单元，242 597个结点；整个模型共包括354 301个单元， 369 626个结点。航行体入水仿真有限元网格见图4。针对模型质量、缩比、速度、入水角度等因素的变化进行仿真研究，获取入水规律，仿真时间为40 ms，间隔0.5 ms读取一次结果数据。航行体入水状态如图5所示，随着航行体入水，液面隆起，干扰导致的涟漪向周围传播。

图4 航行体入水仿真有限元网格

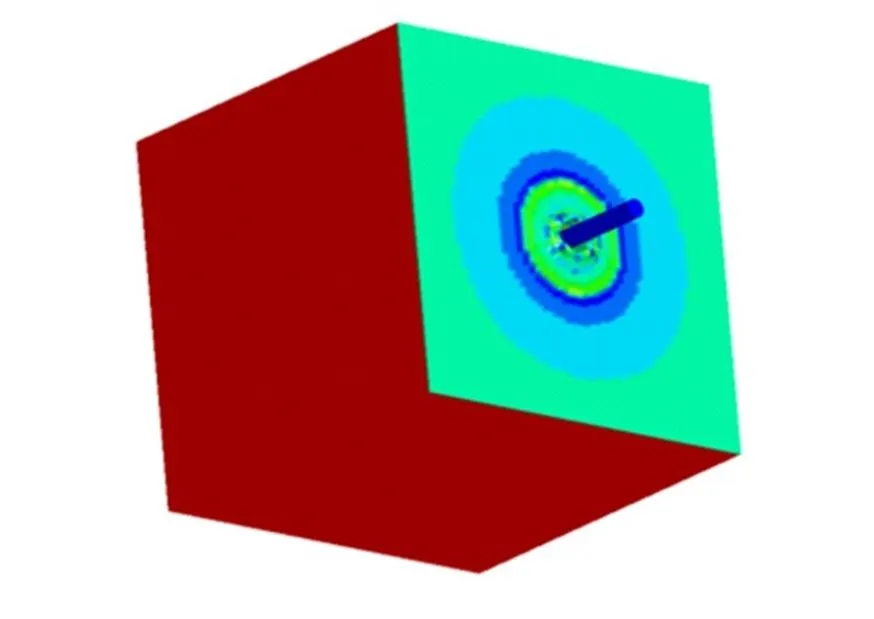
图5 航行体入水状态

共开展了10个工况的仿真研究，其中工况1～3考虑质量因素的影响，工况4和工况5考虑缩比效应的影响，工况6～8考虑入水速度因素的影响，工况9和工况10考虑入水角度的影响。工况2和工况3模型加速度随时间变化曲线见图6。

图6 工况2、3加速度随时间变化曲线

由图6可知，模型入水过程类似经历阶跃力作用，质量越小，阶跃加速度幅度越大。工况4和工况5模型加速度随时间变化曲线见图7，由图7可知，入水过程中，缩比1∶3模型与1∶1模型所受阶跃加速度幅值相当，但在静态过载的基础上还叠加着高频加速度，分析其原因，在高速碰撞计算中，突加载荷引起的强间断及其波传播，会引起数值振荡，与文献[8]中结论相符。

图7 工况4、5加速度随时间变化曲线

通过对各工况下加速度随时间变化曲线进行FFT变换可以得到模型入水过程的静态过载值，该过载值为考虑轴向与法向综合作用的合成过载。模型入水规律仿真结果如表1所示，其中1~4代表不同质量，1~4代表不同速度。工况1～3的仿真结果表明，航行体入水过载与质量成反比，相同速度条件下，质量越小，过载越大。工况4和工况5的仿真结果表明，外形、质量与速度同时缩比后，得到的最大过载值与1∶1模型相同，验证了缩比定律的有效性。工况6～8的仿真结果表明，静态过载与入水速度的平方成正比，与文献[7]中通过试验得到的结论相一致。工况9和工况10的仿真结果表明，垂直90°入水得到的过载稍大于倾斜20°入水，入水角度对过载影响较小。

表1 模型入水规律仿真结果

Tab.1 Simulation Results of Model Water-Entry Law

工况质量/kg入水速度/（m·s-1）静态过载备注 1M1V1275g质量不同 210M1V127.5g 347M1V16g 4M2V242g缩比1∶3模型 527M21.73V242g1∶1模型 6M3V35g入水速度不同 7M32V321g 8M33V346g 9M4V441.2g垂直90°入水 10M4V439.3倾斜20°入水

4 结 论

采用有限元软件LS-DYNA中基于ALE的流固耦合方法，对美国MK25鱼雷模型的入水过程进行了模拟，获取了模型入水过程中的冲击效应、过载及流固耦合形态等结果，验证了仿真方法的有效性。

针对航行体模型的质量、缩比、速度、入水角度等因素进行了仿真研究，结果表明，航行体入水过载与质量成反比，相同尺度、速度条件下，质量越小，过载越大。外形尺度、质量与速度同时缩比后，得到的最大过载值与1∶1模型相同，验证了缩比定律的有效性。仿真结果在静态过载的基础上叠加着高频加速度，分析其原因，在高速碰撞计算中，突加载荷引起的强间断及其波传播，会引起数值振荡。静态过载与入水速度的平方成正比；垂直90°入水得到的过载稍大于倾斜20°入水，与入水速度相比入水角度对过载影响较小。以上研究结果对于开展试验研究及总体设计具有指导意义。

[1] 王永虎, 石秀华. 入水冲击问题研究的现状与进展[J]. 爆炸与冲击, 2008, 28(3): 276-282.

Wang Yong-hu, Shi Xiu-hua. Review on research and development of water-entry impact problem[J]. Explosion and Shock Waves, 2008, 28(3): 276-282.

[2] 潘光, 杨悝. 空投鱼雷入水载荷[J]. 爆炸与冲击, 2014, 34(5): 521-526.

Pan Guang, Yang Kui. Impact force encountered by water-entry airborne torpedo[J]. Explosion and Shock Waves, 2014, 34(5): 521-526.

[3] 孙琦, 周军, 林鹏. 基于LS-DYNA的弹体撞水过程流固耦合动力分 析[J]. 系统仿真学报, 2010, 22(6): 1498-1501.

Sun Qi, Zhou Jun, Lin Peng. Dynamic analysis of fluid-structure interaction for water impact of projectile using LS-DYNA[J]. Journal of System Simulation, 2010, 22(6): 1498-1501.

[4] 张虚怀. 返回舱着水冲击模拟及其影响因素分析[D]. 北京: 清华大学, 2009.

Zhang Xuhuai. Water impact simulation of spacecraft capsule and the analysis of its factors influence[D]. Beijing: Tsinghua University, 2009.

[5] 李裕春, 时党勇, 赵远. ANSYS11.0/LS-DYNA基础理论与工程实践[M]. 北京: 中国水利水电出版社, 2008.

Li Yuchun, Shi Dangyong, Zhao Yuan. Basic theory and project practice of ANSYS11.0/LS-DYNA[M]. Beijing: Water Resources and Hydropower Press, 2008.

[6] 麻震宇. 超空泡航行体结构动力学仿真研究[D]. 北京: 国防科学技术大学, 2012.

Ma Zhenyu. Numerical research on dynamics of structures for supercavitating vehicles[D]. Beijing: National University of Defense Technology, 2012.

[7] John G. Water-Entry pitch modeling[J]. J. Hydronautics, 1968, 2(2): 87-92.

[8] 王爱俊, 戴棣, 乔新. 高速碰撞中Lagrange有限元方法及其应用[J]. 南京航空航天大学学报, 1998, 30(3): 675-679.

Wang Aijun, Dai Di, Qiao Xin. Lagrangian finite element method and its application in high velocity impact phenomena[J]. Journal of Nanjing University of Areonautics & Astronautics, 1998, 30(3): 675-679.

Study on High-speed Water Entry Law of Trans-media Vehicle Based onFluid Solid Coupling

Wei Hong-liang, Zhao Jing, Xu Zhi-cheng, Yu Qi-dong, Li Ming

(R&D Center, China Academy of Launch Vehicle Technology, Beijing, 100076)

To address the problem of fluid solid coupling during vehicles’ high-speed water entry, based on LS-DYNA software using fluid solid coupling method of ALE，the water entry process of US MK25 torpedo model is simulated. The impact effect and acceleration varying with time are both obtained. The results exhibit different forms of fluid solid coupling, and thus the validity of the simulation is verified. Then the influences of mass, scaling effect, velocity, and water entry angle for trans-media vehicle model are simulated using the ALE method. The simulation results show that the key point to determine acceleration of water entry is velocity, where the influence of water entry angle is minor. The results also verify the validity of scaling law.

Arbitrary Lagrange-Euler; fluid solid coupling; trans-media; high-speed water entry

V412

A

1004-7182(2020)02-0033-05

10.7654/j.issn.1004-7182.20200207

魏洪亮（1978-），男，博士，高级工程师，主要研究方向为载荷与力学环境设计、结构强度设计、水弹道与水载荷设计。

赵 静（1981-），女，博士，高级工程师，主要研究方向为计算流体力学。

徐志程（1982-），男，高级工程师，主要研究方向为水动力与水下发射总体设计。

俞启东（1985-），男，高级工程师，主要研究方向为水动力与水下发射总体设计。

李 明（1986-），男，博士，高级工程师，主要研究方向为流固耦合动力学。

2018-04-08；

2018-07-09

基础科研项目（JCKY2018203B025）