一种改进的开关磁阻电机无位置传感器控制方法

苗 盛，熊立新,，张明魁，夏 强

(1.山东理工大学 电气与电子工程学院，山东 淄博 255000；2.山东科汇电力自动化股份有限公司，山东 淄博 255087)

0 引 言

开关磁阻电机(SRM)是一种变磁阻双凸极式的电机，与其他电机相比，SRM电机结构简单牢固，成本低廉，性能优异，兼具交流和直流电机的优点。近年来随着电力电子技术的发展，开关磁阻电机受到了广泛关注，在机械机床、风力发电、航空航天等领域逐渐得到应用。

开关磁阻电机的运行原理是根据电机本体定转子相对位置，通过开关磁阻电机控制器对开关管施加换相信号，实现相绕组电流的轮流导通与关断。传统的定转子位置检测方案采用机械装置检测转子位置，其测量电路有接近开关式、旋转变压器式、光敏及霍尔位置式传感器，这些形式的传感器安装在电机本体上，不仅增加了电机结构的复杂度、生产成本和安装工作量，而且电机运行中易受干扰，降低了系统可靠性。基于以上原因，无位置传感器技术成为国内外学者研究的热点之一。

目前国内外已有许多无位置检测方案，如基于激励相检测的相电流波形法[1]、磁链法[2-3]、状态观测器法[4-5]；非激励相检测的脉冲注入法[6]；附加元件法[7]以及基于神经网络的智能控制检测法[8]。这些方法各有优缺点，例如简化磁链法与智能控制检测法需要大量的离线调试工作；状态观测器法计算复杂，对处理器实时性等要求很高，并且需要对电机模型等相关参数有深入的了解，整体动态性能较差；附加元件法需要添加额外设备，增加了系统的的复杂性和成本。其中脉冲注入法原理简单，无需外加元件，具有良好的发展前景，文献[9]在两个非导通相同时注入脉冲，根据两相响应电流大小的逻辑关系判断转子位置，这种方法解决了电压波动的问题，但未考虑上一导通相续流电流对电流比较造成的影响；文献[10]提出了一种电流斜率差值的脉冲注入法，该方法利用脉冲上升和下降的电流斜率之差，消除了反电动势的影响，但未考虑母线电压波动造成的误差；文献[11]提出了一种变电流双阈值脉冲注入法，该方法考虑了母线电压变化对电流阈值大小的影响，设定了双阈值将电感区间重新进行了划分，避开了电机定转子在齿与齿对齐和齿与槽对齐时电感值大小变化不明显、响应电流值区分度不大，位置估算精确度下降的问题；文献[12]提出了一种变脉冲宽度的方法，解决了响应电流较小，峰值变化不明显的问题，但仍存在单阈值方法受电路偏移、电压波动的问题。

本文以6/4结构的SRM为例，对传统的脉冲注入法进行了改进，提出了一种具有通用性的两相比较四点采样的开关磁阻电机无位置检测方案，并使用Matlab/Simulink软件进行了模型搭建与仿真验证，结果表明本方法可以有效解决电压波动、干扰噪声、电路漂移等引起的脉冲注入法实用性差、换相点模糊的问题。

1 脉冲注入法原理

开关磁阻电机的单相电压平衡方程为

U=Ri+Ldi/dt+iωdL/dθ

(1)

式中，U为母线电压，R为相绕组电阻，i为相绕组的电流，L为电机的电感，θ为转子角度，ω为角速度。

传统的脉冲注入法需要向电机非激励相注入高频脉冲，由于其注入时间极短，所引起的响应电流小，负转矩可忽略不计，且当电机工作于低速时，上式可忽略掉右侧第一项与最后一项，化简为

U/L=di/dt=Δi/Δt

(2)

因此当母线电压U不变，单个脉冲注入时间Δt一定时，电机的电感值L与响应电流峰值成反比。图1为理想线性模型下SRM高频激励脉冲与响应电流峰值在转子不同位置处的关系示意图。

图1 三相电感及响应电流峰值示意图

由上图可知，响应电流的峰值随着三相电感周期性的改变，也呈现出一种周期性变化的趋势，这使得我们可以从中解算出转子信息。传统的单阈值脉冲注入法即通过事先离线测得换相电感位置处所对应的响应电流峰值大小，并将其作为换相阈值存储，电机实际运行时向下一导通相注入检测脉冲，检测脉冲关断前对响应电流的峰值进行一次采样，并与换相阈值作比较，当测量值达到阈值时，即认为转子到达换相位置，此时进行换相操作，并继续向下一导通相注入检测脉冲。

但在实际运用时，由于SRM电机所处环境存在母线电压波动、电磁噪声、调理电路漂移等众多问题，这些干扰使得响应电流的测量值存在偏差，如果仅仅通过单采样点的电流值与阈值作比较时，易导致换相位置估算误差较大，电机会提前或延迟换相，影响系统效率与可靠性。同时单阈值方法需要离线测量存储换相阈值，较为繁琐，不同的电机、不同的工作电压会具有不同的阈值，根据阈值换相存在着换相点模糊的隐患，难以适应现场电压波动大的情况。

2 两相注入电流斜率比较法

为解决以上问题，提高脉冲注入法的实用性，本文对传统的脉冲注入法进行了改进，即在电机运行时同时向两个非导通相注入脉冲，每一相的注入信号都进行双点采样计算电流斜率，通过比较两相电流斜率的变化来实现换相点的精确判断。

2.1 换相控制方法

由式(2)我们可知：当母线电压U不变时，电感值L与响应电流的斜率成反比，两者在不同位置的对应关系同样可参照图1。根据此原理，换相方案可转换为对非导通相斜率大小关系的判断。图1中已将三相电感周期划分为6个区间，例如A相导通于2区间、3区间时，B相脉冲响应电流的斜率始终大于C相响应电流的斜率，但当转子到达3区间与4区间交界处时，B相与C相响应电流斜率相等，到达4区间后，变为C相响应电流斜率大于B相斜率。因此可以使A相导通于2、3区间，B相导通于4、5区间，将B、C间响应电流斜率大小关系作为判断换相的条件，并以此类推。

在两相比较的方法下，由于是同时注入两个非导通相，即使存在母线电压波动，对两个非导通相而言，电压大小是一致的，因此两非导通相响应电流斜率大小的相对关系并不会改变，所以能克服母线电压波动带来的缺陷，并且换相条件明确，不存在单阈值换相点模糊的缺点。

同时本方法是在SRM电机单相轮流导通的条件下，每个脉冲注入期间即响应电流上升阶段，对非导通相的响应电流分别采样两次，得到一相的i1、i2和另一相的i3、i4，两次采样的时间间隔固定为Δt1，利用两次采样值差值与对应时间差值的比值，据式(2)便可求出两非导通相响应电流的变化率，并加以比较。若在采样电流期间存在噪声干扰与电路漂移，使得采样值i1和i2偏差都为Δix，采样值i3和i4偏差都为Δiy，此时四点采样方法下的电流变化率仍不变，因此可有效克服电路漂移等干扰。

[(i1+Δix)-(i2+Δix)]/Δt1=(i1-i2)/Δt1

(3)

[(i3+Δiy)-(i4+Δiy)]/Δt1=(i3-i4)/Δt1

(4)

当两相响应电流的斜率关系满足换相条件时，证明转子到达换相位置，这时应关闭当前导通相，开通下一相为新的导通相，同时脉冲注入相也变更成新的非导通相。本文选取开通角为15°，关断角为45°，各相轮流导通两个区间。除此以外，为防止上一导通相关闭后续流电流影响换相判断，当上一导通相续流电流下降至接近于0的阈值Ith后，才开始对非导通相注入脉冲，综上所述，电机运行时的换相逻辑如表1所示。

表1 换相逻辑表

2.2 启动相选择方法

在电机初始启动时，需要知道转子位置确定最初的启动相，无位置运行方式下没有位置传感器回馈位置信号，结合前文运行时的换相控制方法，表2给出了电机初始启动时刻的位置判断逻辑：在上电运行初始时刻，向各相绕组同时注入短时间的高频脉冲，采样电流计算斜率，判断转子所在区间，选择启动相。

表2 启动相选择方法

3 仿真验证与误差分析

为验证上述控制方法的正确性和可行性，本文使用Matlab/Simulink进行了模型搭建与仿真，该模型设计基于三相6/4开关磁阻电机，额定功率15 kW，定转子对齐位置最大电感7 mh，不对齐位置最小电感0.7 mh，定子绕组采用转速电流双闭环调速系统，且转速调节器使用PI控制方式，转速调节器根据给定转速输出参考电流值，电流环采用电流斩波控制方式(CCC)，滞环宽度为±1.5 A，根据参考电流值和反馈电流控制开关的通断以达到调节电流大小的作用，最大电流限制为60 A，功率变化器模块由240 V直流电源供电，脉冲注入频率选择为10 kHz，占空比为15%，为验证该方法相较于单阈值方法能有效对抗噪声、电路偏移等问题，减小误差，电流采样通道添加了噪声发生器来模拟干扰环境。系统整体模型图如图2所示。

图2 系统整体模型图

电机在运行过程中，在一相导通期间，经过上一导通相续流电流降至阈值Ith(设为0.1 A)后，开始向非导通相注入脉冲，同时对响应电流采样计算电流斜率，直至两非导通相电流斜率满足换相条件，完成换相操作，电机运行期间的三相电流图如图3所示。

图3 三相电流波形图

将脉冲发生器分别延时1 μs和15 μs，且将其上升沿作为采样保持器使能信号，对响应电流完成脉冲单个周期上升阶段1 μs时刻和15 μs时刻的采样，后续依据式(2)计算出电流斜率，脉冲响应电流采样和斜率计算模块以及斜率计算图如图4与图5所示。

图4 电流采样和斜率计算模块

图5 斜率计算图

无位置控制方式下电机转速的估算为

nest=60×Δθ/360×ΔT=Δθ/6ΔT

(5)

式中，Δθ是两相导通间转子转过的角度，对于6/4的开关磁阻电机来说，该角度为机械角度30°，ΔT是相邻脉冲间的时间差，即上式用相邻相导通的角度差除以相邻相导通的时间差对电机进行转速估算。转速估算模块利用三相导通信号上升沿对当前时间进行采样，完成对转速的估算，实际转速与估算转速对比图如图6所示。

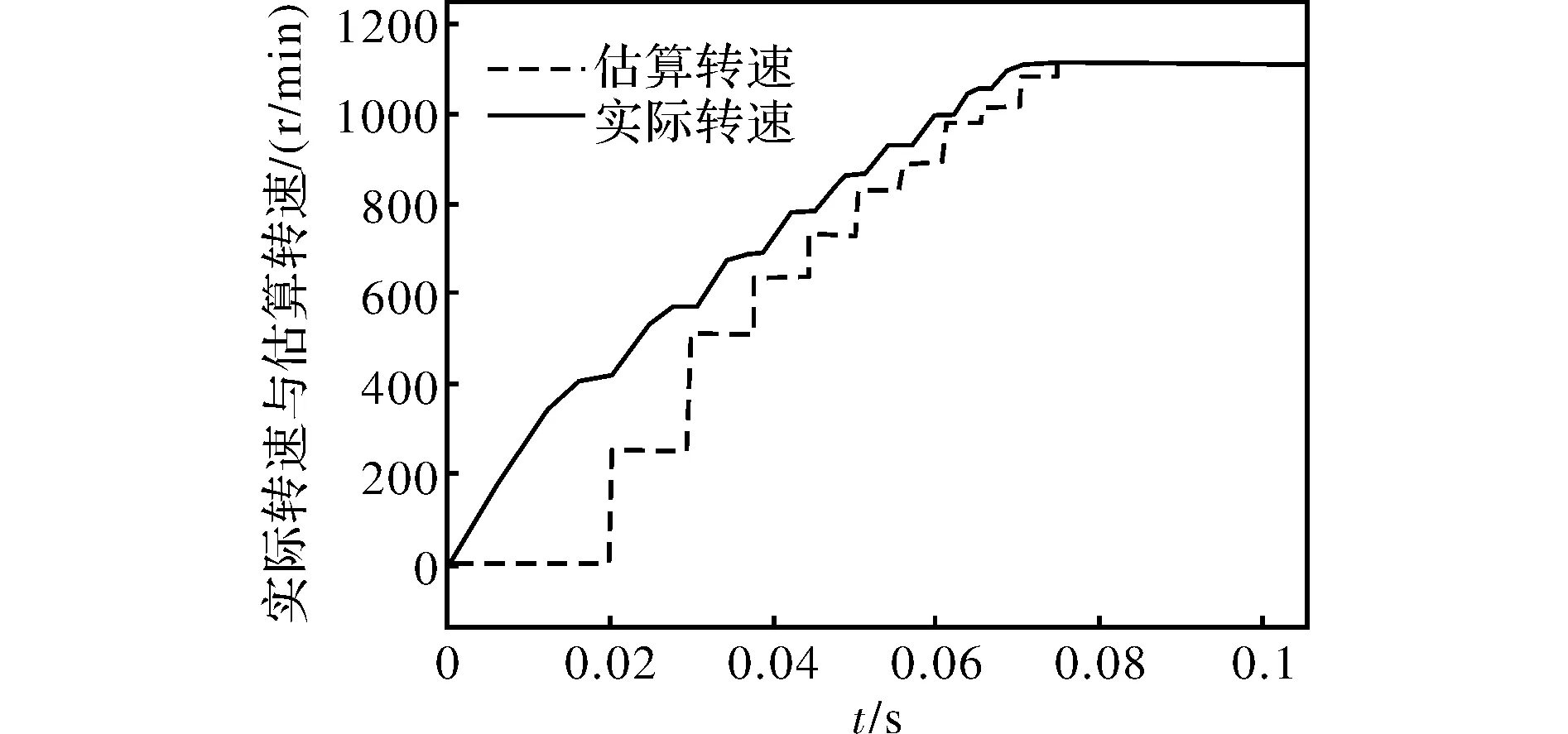
图6 实际转速与估算转速对比

在无噪声干扰时，对电机工作在500 r/min、1000 r/min、1500 r/min三种转速，分别测量了20个换相角度误差数据样本，并搭建了单阈值脉冲注入法模型，同样完成上述误差测量，两种方法在不同转速下的平均绝对误差对比如表3所示，可以看出，此时两种方法在不同转速下误差相差不大。

表3 无噪声平均绝对误差对比表

为验证新方法相较于单阈值方法在噪声干扰环境下的优越性，在三相电流采样通道分别加入了不同的噪声干扰，例如A相所加噪声波形如图7所示。

图7 噪声波形图

当存在噪声干扰时，重复上述误差测取步骤，两种方法在不同转速下的平均绝对误差对比如表4所示，此时单阈值方法误差明显增大，而新方法误差变化不明显。

表4 有噪声平均绝对误差对比表

4 结 论

通过两相注入脉冲进行电流斜率比较的方法来实现SRM无位置传感器控制，本文搭建模型进行了仿真，并与单阈值脉冲注入法对比分析，测量了两种方法在无噪声和有噪声、电路偏移环境下的换相角度误差，仿真结果表明该无位置控制方法能正常运行，并能有效克服干扰带来的采样电流值偏差问题，同时两相比较方式下可以有效减少电压波动和换相点模糊的问题，相较于单阈值方法有更小的位置估算误差，具有一定的工程应用价值。