基于OSELM 的路段行程时间预测算法仿真实验和算法评估

●阳敏辉

一、数据集的选取

为了验证算法的可行性和准确性，本文从Regiolab-delft 平台上选取了A13 快速路上两组数据集用来建模：一天的数据以及一个星期的数据（7 天数据为训练集，另加1 天数据为测试集）。一天的数据为2017年7月1日0:00 至24:00 一共476 组行程时间数据，其中前408 组数据作为训练集，后面68 组数据作为测试集；一个星期的数据为2017年6月1日到6月8日一共280 组6:00-9:00 早高峰期数据，前7 天一共245 组数据作为训练集，后面一天35 组数据作为测试集。数据集说明如表1。

表1 数据集说明

二、实验及结果分析

（一）一天数据集实验及结果分析

1.三种算法的参数设置。数据集中共有476 组数据，将前408组数据作为训练集，后68 组数据作为测试集，三种算法参数设置如下：（1）OSELM-TTP：算法中要设置的参数为隐层神经元个数和激励函数，通过试凑法得到的隐层神经元个数为8，学习函数设为sin。（2）OSVR：设置的核函数为RBF，参数C 和ε 分别为0.07 和0.01。（3）BPNN：MATLAB 中用newff()函数来建立3 层的BPNN 预测算法，在参数设置时，将隐层神经元个数设为3，学习函数为learngdm，输入层、隐层和输出层的激活函数分别为：tansig、logsig、tansig。训练函数设置为traingd。

2. 实验及结果分析。实验得到的预测值与真实值对比如图1、2、3。图中，横坐标表示预测行程时间值的总数，而纵坐标表示的是预测的行程时间，其单位为m。红色曲线代表待机的经过归一化预处理之后的真实数据，而蓝色曲线代表预测算法得到的行程时间预测值。从图中可以看出，添加了实时序列机制、自适应丢弃机制和优选激励函数机制的OSELM-TTP 算法，其预测结果基本接近实际监测数据。而基于OSVR 预测的数据浮动比较大，BPNN 预测曲线与真实数据之间的误差较大。三种预测算法的评估指标对比如表2 所示。

表2 一天的数据集OSELM-TTP、OSVR、BPNN 评估指标对比

从表2 分析得到：（1）从MSE 可以看出，OSELM-TTP 得到MSE 比OSVR 和BPNN 小，相比之下，OSELM-TTP 预测效果最好。（2）从MAE 和MRE 可以看出，OSELM-TTP 的值比BPNN 要小，两者相差不大，而BPNN 的值比OSVR 要小，表明OSELM-TTP 预测效果最好。而由于OSVR 在预测时波动较大，值也就最大，因此得到的效果最差。（3）从EC 可以看出，ELM的EC 值为0.989171566，大于0.9，而SVR 和BPNN 的值分别为0.979352813 和0.807924733，均低于OSELM-TTP 的EC 值。表明OSELM-TTP 得到的预测值和真实值的拟合效果最好，精确度比OSVR 和BPNN 的精确度要高。

（二）一周数据集实验及结果分析

表3 一周的数据集OSELM-TTP、OSVR、BPNN 评估指标对比

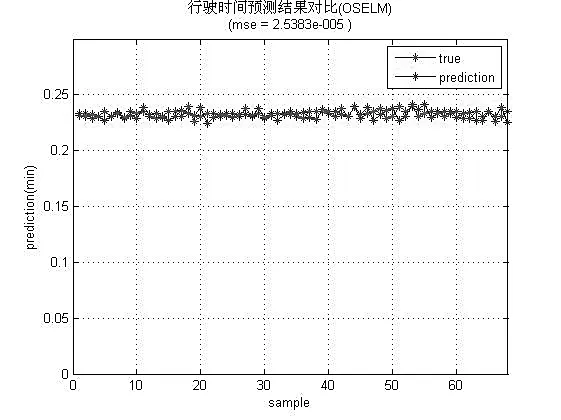
图1 一天的数据集中OSELM-TTP预测值与真实值对比图

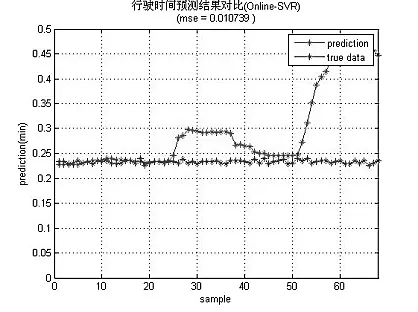
图2 一天的数据集中OSVR算法预测值与真实值对比图

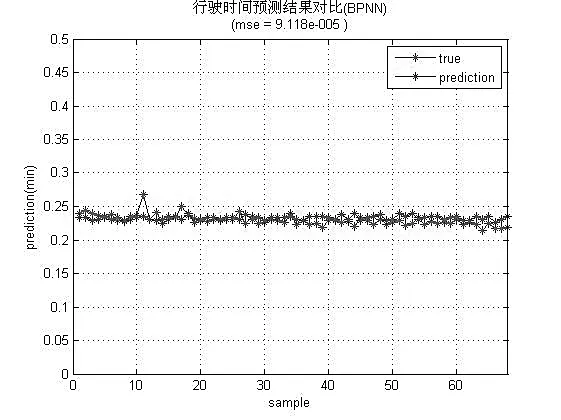
图3 一天的数据集中BPNN算法预测值与真实值对比

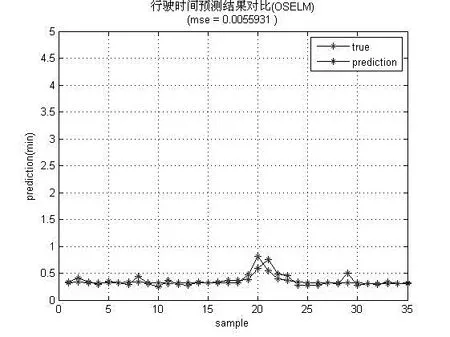
图4 一周的数据集中OSELMTTP 算法预测值与真实值对比图

图5 一周的数据集中BPN N 算法预测值与真实值对比图

图6 一周的数据集中OSVR算法预测值与真实值对比图

1. 三种算法的参数设置。数据集中共有280 组数据，将前245 组数据作为训练集，后35 组数据作为测试集，三种算法参数设置如下：（1）OSELM-TTP：算法中要设置的参数为隐层神经元个数和激活函数，通过试凑法得到的隐层神经元个数为10，学习函数设为sin。（2）OSVR：设置的核函数为RBF, 参数C 和ε 分别为0.3 和0.01。（3）BPNN：MATLAB 中用newff()函数来建立3 层的BPNN 预测算法，在参数设置时，将隐层神经元个数设为8，学习函数为learngdm，输入层、隐层和输出层的激活函数分别为：tansig、tansig、tansig。训练函数设置为traingdm。

2.实验及结果分析。实验得到的预测值与真实值对比如图4、图5、图6。横坐标表示预测行程时间值的总数，而纵坐标表示的是预测的行程时间，其单位为m。从图中可以看出，OSELM-TTP 的预测曲线与真实数据曲线的波动相似，而OSVR 算法在数据出现波动时，预测的曲线却呈现出一个平滑的状态，这说明算法时变性不强，而BPNN 预测的曲线波动较多，不能体现BPNN 预测的稳定性，因此，综合来看，OSELM-TTP 的预测结果更接近于真实结果，预测的精度最高。三种预测算法的评估指标对比如表3 所示。

从表3 分析得到：(1)从MSE 可以看出，OSELM-TTP 得到的值为0.005594，而OSVR 和BPNN 得到的值分别为0.008720 和0.030222，相比之下，OSELM-TTP 的误差最小，预测精确度最好。(2) 从MAE 和MRE 可以看出，OSELM-TTP 的值比OSVR 要小，两者相差不大，而OSVR 的值比BPNN 要小，表明OSELM 预测的效果最好。(3) 从EC 可以看出，OSELM-TTP 的EC 值为0.897106，而OSVR 和BPNN 的值分别为0.869912 和0.785791，均低于OSELM-TTP 的EC 值。表明OSELM-TTP 得到的预测值和真实值的拟合效果最好，精确度比OSVR 和BPNN 的精确度要高。

综合以上两种数据集的实验结果，可以表明OSELM-TTP 所得到的预测结果比OSVR 和BPNN 更接近于真实数据。因此OSELM-TTP 在行程时间预测具有实际应用价值，适用于行程时间预测。