亏格4周期纤维的陈数结果

张宇鑫

【摘 要】 2012年，陆俊、谈胜利提出了对任意奇异纤维关于陈数上下界的猜想。本文主要计算 了亏格4的周期纤维的陈数和Euler - Pomcare特征标，并结合龚成亏格2与符玄龙亏格3的分类结果，验证了在亏格4周期纤维的情况下，陆俊、谈胜利猜想的正确性。

【关键词】 陈数;周期纤维;纤维化

在复代数曲面的研究中，（代数）纤维化是一类常见的研究对象。我们称光滑既约的射影代数曲面S到光滑既约的射影代数曲线，C的满的态射?：S是纤维化，且? 的每条纤维都是连通的[1]。与射影代数曲面的双有理几何的情况不同，纤维化的理论可以说是研究代数曲面上有理函数的几何学[2]。事实上，因为非常的有理函数可以看作曲面到射影直线的支配的有理映射，而通过奇点解消以及Stein便可以得到上面的纤维化的形状。由于代数簇的研究本质上是其上有理函数的研究，故纤维化的研究可以反映曲面的数值不变量[3]。下面考虑纤维化?：S，由于/的临界值的全体是C的Zariski闭集，故是 有限集。故 ? 的一般纤维都是光滑射影曲线。我们称 ? 是亏格g的纤维化，若其一般纤维F的亏格g，这与一般纤维的选取无关。特别地，若纤维化 ? 的亏格为0，即 ? 的每条纤维都是P时，称 ? 为直纹;称亏格为1的纤维化为椭圆纤维化。当 ? 是亏格g的 纤维化时，? 的任意纤维的算数亏格也为g 。

一、亏格相关定理

我们有以下重要的引理：

由算数亏格这一整体的不变量，我们可以得到曲面的奇点解消理论：光滑代数曲面上的既约曲线的奇点可以通过有限次blowing up解消，进一步的，曲面间的双有理映射都是有限个blowing up以及其逆映射blowing down的复合。通过blowing up可以产 生（-1）曲线，反之，Castelnuovo收缩定理证明了任意（-1）曲线也都是通过blowing up 产生的。由此，曲面的极小模型不存在（-1）曲线，于是我们便得到了相对极小模型的观点：即称纤维化 ? ：S是相对极小的，如果 ? 的每条纤维都不含（-1）曲线。

类似极小模型时的情况，对于任意的纤维化 ?0：S，一定存在其相对极小模型[2]：因若?0存在（-1）曲线，E0将其收缩，得到的新的光滑曲面X1与纤维化 ?1：S且满足 ?0=?10。其中 ：是收缩映射。接下来归纳的，收缩 ?i中的（-1）曲线，Ei，最终可以得到一个不含（-1）曲线的代数纤维化。另一方面，若g>0，则相对极小模型唯一。但当g>0时，相对极小模型可能是不唯一的。然而这样的纤维化有非常 简单的结构，即f是一个直纹，并且可以证明任意g>0时，两个相对极小模型可通过有限次基本变换相互转换。这样我们在一定程度上得到了更适合数值不变量的分类。

接下来，我们引入稳定性的概念。稳定性本来是构造曲，局部自由层模空间时引入的概念，但在纤维化理论中有很重要的应用。我们称相对极小纤维F是半稳定的，若F 是既约，具有正规交，任何相对极小纤维F总是可以通过blowing up其上的奇点，得到一个只有结点的纤维F，并且F的每条（-1）曲线至少要和其他分支相交3个点，这样的F是唯一确定的，称之为F的极小正规交模型。

为计算不变量，我们介绍一些数值不变量：设n是基变换，F是?的奇异纤维，我们定义F的一些数值不变量陈数与Euler-Pouncare'特征标，其定义如下：

二、周期纤维的陈数

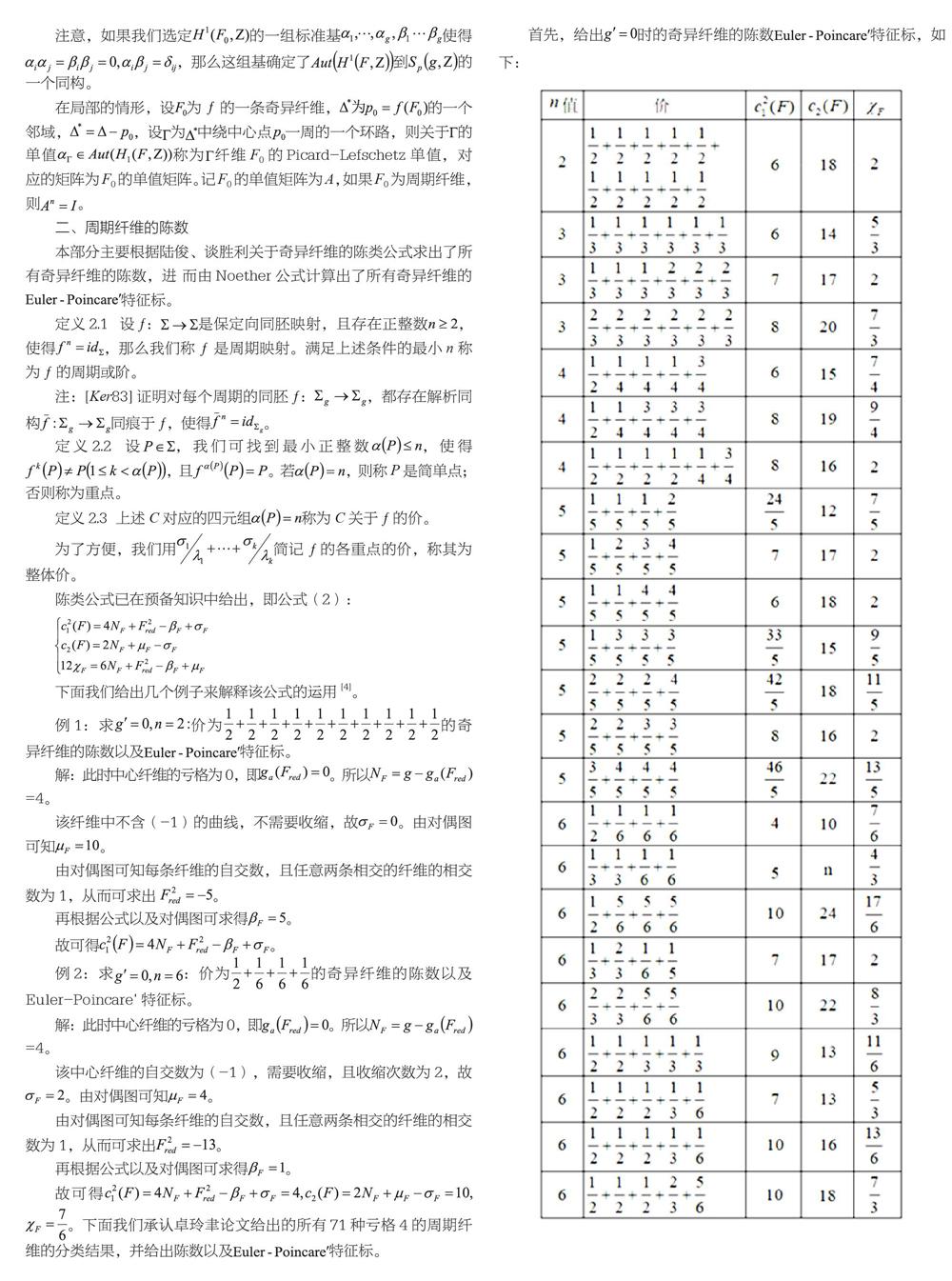
本部分主要根据陆俊、谈胜利关于奇异纤维的陈类公式求出了所有奇异纤维的陈数，进 而由Noether公式计算出了所有奇异纤维的特征标。

【参考文献】

[1]J.Harvey.Cyclic groups of automorphisms of compact Riemann surfaces[J].Quart.J.Math. Oxford Ser.1996（2）：86-97.

[2]T.Ashikaga，M.Ishizaka.Classification of degenerations of Castelnuovo surfaces[M]. J. Math.Soc.Japan，1991（3）：229-246.

[3]Sheng-Li Tan.Chern numbers of a singular fiber，modular invariants and isotrivial families of curves[J].acta mathematica vietnamica，2010（10）：159-172.

[4]肖刚.代数曲面的纤维化[M].上海：上海科技出版社，1992（3）：72-80.

[5]龚成.上具有兩条或三条奇异纤维的曲面纤维化[D].华东师范大学，2012.

[6]符玄龙.曲线上具有两条奇异纤维的亏格3纤维化[D].华东师范大学，2012.

[7]卓玲聿.亏格为4的周期纤维的分类及其应用[D].苏州大学，2012.