厘“逆”之理实“顺”之基——《加法和减法》教学与评析

执教/朱孟迪 评析/刘善娜（特级教师）

《加法和减法》这节课有两个重点：其一是建构加法和减法的意义，其二是回顾并整理加、减法各部分间的关系，建立完整的知识结构。教材以青藏铁路为现实背景，解决西宁——格尔木——拉萨铁路线问题。先解决西宁到拉萨的铁路长多少千米，以此来建构加法的意义，接着变换已知数和未知数，呈现问题，在解决的过程中引导学生概括减法的意义。在此基础上，回忆加、减法中的各部分名称，探究各部分之间的关系。

这节课常见教学流程是：呈现加法学习素材→建构加法概念→举一反三丰富素材→发现加法各部分关系→建构减法概念→讨论各部分关系→练习深化。但是这样的过程会因为学习内容缺乏挑战性、概念的抽象过程具有枯燥性而让学生觉得索然无味。那么，是不是能找到一个点，将散乱抽象的点状学习材料都“串”起来呢？我们进行了这样的尝试：

一、课前谈话初识“逆”

师：（课件出示“逆”）同学们，认识这个字吗？说一说你对它的理解？

生：倒过来、反过来、反着来。

师：数学中，有时也会用到这个字，一起读一读：“减法是加法的逆运算。”你能根据自己的经验解释一下这句话吗？你可以列一列算式，画一画草图，写一写文字，来表示自己的想法。

二、自主表征感知“逆”

作品一：（算式）

5+3=8 8-3=5

生：加法是把两个加数加起来，减法是从和里面减去一个加数。

师：你的意思是加法是告诉加数和加数，求和；而减法呢？

生：减法是告诉和与其中一个加数，求另一个加数。

师：是吗？让我们找一找——减法中的8，相当于和；减法中的3，相当于加数；减法中的结果，相当于另一个加数。形成板书：

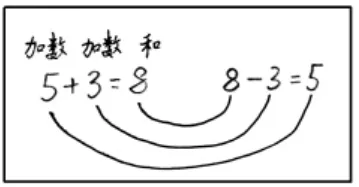
师：他发现——加法是告诉我们加数和加数，求和；减法是告诉我们和与其中一个加数，求另一个加数。这就是你们心目当中的逆运算，对不对？

作品二：（线段图）

师：这幅线段图逆在哪里呢？

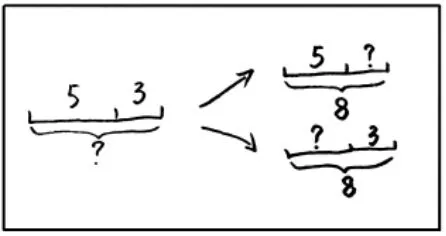
生：左边是把两个数5 和3加起来；右边是已知一个加数5与和8，求另一个加数，或者是已知一个加数3 与和8，求另一个加数。

师：你的意思是左边这幅图告诉我们加数与加数，求和；右边两幅图告诉我们和与一个加数，求另一个加数。这位同学还从一道加法，变出两道减法来，真不错。

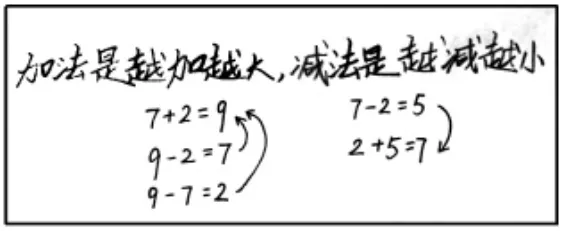
作品三：（文字）加法是越加越大，减法是越减越小。

生：加法是越加越大，减法是越减越小，所以减法是加法的逆运算。

师：你能举个例子吗？

（7+2=9 7-2=5）

师：你能看着这个加法算式（7+2=9），变出两道减法吗？

生：9-2=7，9-7=2。

师：你们看下图，一变就变出了逆的感觉。同学们看看，这道题（7-2=5）是这道题的逆运算吗？（不是的）那它是怎么逆过来的呢？（2+5=7）

三、厘清关系构建“逆”

师：同学们真厉害，借助自己的经验，想到多种方法来解释“减法是加法的逆运算”。现在你来说说看，什么是加法？什么又是减法？

师：你们看，减法好可怜呀！它没有专属自己的核心词，而是仅仅依靠加法中的“加数”、“和”这样的核心词。正因为如此，更让我们感受到减法是加法的逆运算。来，让我们再来读一读——你读出“逆”的感觉了吗？真好！在数学上，相加的两个数叫做加数，加得的数叫做和。

四、充实素材再议“逆”

题组1：在求解中强化关系理解。

快问快答——已知什么？要求什么？

【设计意图：这是一组针对性练习，针对加减法的各部分关系而设计。学生回答后要追问：“你认为哪些题要逆过来进行思考？”进一步引导学生关注“逆”关系。】

题组2：具体问题中抽象内化运算意义。

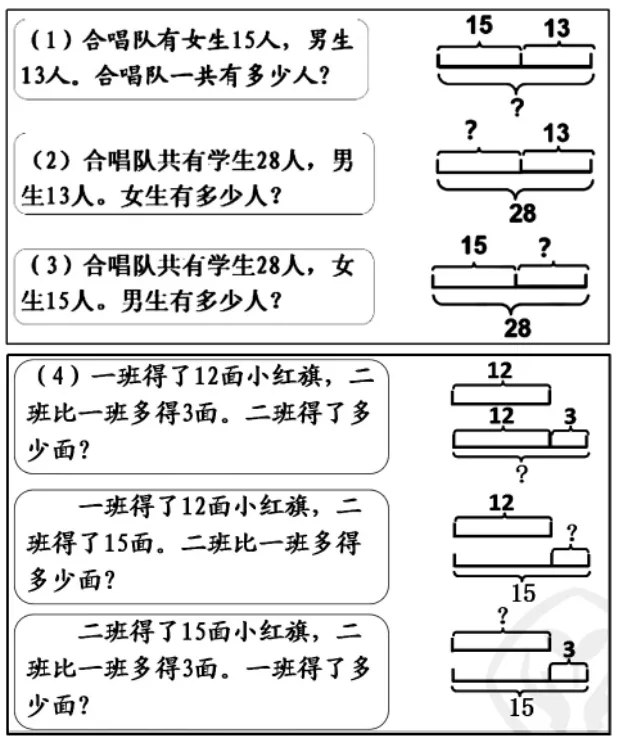
【设计意图：这一层练习，分为两层推进，感受不同的“加法”和“减法”结构所体现的相同意义。学生发现同一个“数学故事”，随着信息和问题的交换，解决问题的方式就会“互逆”。线段图，则使学生对加减法的意义有更好的理解。】

题组3：编题中感受“互逆转化”。

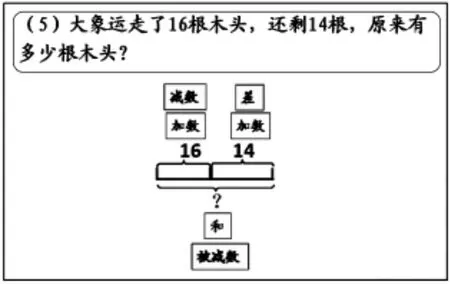
【设计意图：“运走”、“剩下”是减法问题常见的信息描述语。求“原来”是逆推。通过这一题的解答以及随后的自行编题“你能把这道题的问题和信息逆过来，改编成用减法解决的问题吗”让学生从题组中对比感知问题中蕴含的加减法关系。】

五、理清关系深化“逆”

1.回忆旧知，进行联系。

师：同学们，回忆旧知，你们有没有发现“减法是加法的逆运算”这个原理，我们似曾相识？

检验减法计算结果是否正确，我们可以用加数来验算。一图四式中，既有加法，又有减法，计算减法时，也可以利用逆运算快速得到答案。

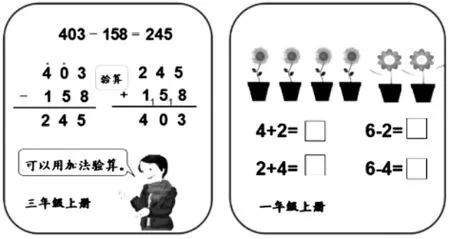
2.整合理解各部分关系。

（1）动笔解答。

23 +（ ）=125，125 -（ ）=23，125+23=（）；

（）-125=23，（）-23=125，125-23=（）。

（2）分类观察。

师：根据答案给它们分分类，你有什么新的发现？

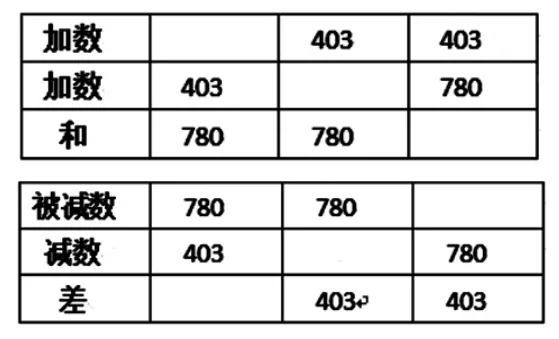
生1：我发现，和=加数+加数，加数=和-另一个加数；被减数=减数+差，减数=被减数-差，差=被减数-减数。

生2：我发现，求和与求被减数竟是一样的！

师：有这么神奇吗？

（学生再观察算式，并形成这样的板书：和=加数+加数 被减数=减数+差）

生3：我还发现，求加数，与求差，求减数，也是一样的。

（板书：加数=和-另一个加数，减数=被减数-差，差=被减数-减数）

师：同学们，这些加减算式中，竟然还存在如此多的关系，我们看到了它们“变中有不变”的意蕴！现在，你认为加法和减法，哪个更基础？（加法）是呀，有时它这样呈现——告诉我们两个加数；有时它这样呈现——只告诉我们一个加数，只要我们找到基本关系，火眼金睛进行辨析，就可以很快得到答案。你掌握这些方法了吗？马上完成“学习单”第2 题。

?

六、强化练习完善“逆”

1.算一算，破难点。

【设计意图：针对学生的易错点设计。追问“为什么题目中有‘加’，却用减法做”“为什么题目中有‘减’，却用加法做”？让学生明白加减法互逆关系，如第2 小题的“我”既可以理解成“求和”，也可以理解成“求被减数”，能加深互逆关系理解。】

2.填一填，练重点。

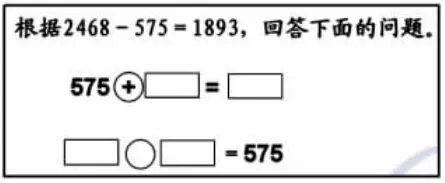
【设计意图：通过追问第2 小题“为什么想到是一道减法呢”，学生既可以想到“被减数-差=减数”，也可以想到“求一个加数要用减法”。】

【设计意图：利用没有学过的异分母分数加法，考查学生灵活应用加减法的关系来解决问题的能力，尤其是呈现图形之间的关系，更是考查了学生对加减法意义与各部分关系的理解程度。】

【评析】

这节课的学习内容看似非常简单，课后习题就算不教学生也会做，但整个学习材料较多、板块琐碎，加减法的“意义”、“关系”的表述都比较抽象，与儿童的经验性语言并不契合，都需要加以引导和提炼。因此寻求清晰的教学路径、生动地组织起所有学习材料，是执教者设计本课教学的出发点。

朱老师寻求到了很好的一个点，使整节课有“探”有“论”，有概念理解也有难点挑战，将一节看似无味的课上得有深度又有趣味。而这个“点”，就是“减法是加法的逆运算”的“逆”。这个“逆”关系不仅体现在“加减法的意义”上，更体现在“加减法各部分之间的关系”上。“逆”为核心的教学，就是关系角度的教学。学生借助“逆”关系的探究，建构加、减法的概念，形成加减“逆”关系的感悟。与此同时，借助“逆”关系，架起了加法内部关系式、减法内部关系式、加减关系式的桥梁，形成了以“加法模型”为基础的加减法关系网。主要凸显了三个特色：

1．“逆”字切入，探究先行。

为什么说“减法是加法的逆运算”？这个问题并不好回答。所以，朱老师分两步走：你认识的“逆”字是什么意思→“逆运算”又是什么意思。学生对“逆”字的理解，基本会表达为“逆反”、“相反”、“反着来”。这番轻松的对话，有助于所有学生对“逆运算”的理解。而什么是“逆运算”，朱老师则放手让学生自己探究“你能根据自己的经验解释一下这句话吗？你可以列一列算式，画一画草图，写一写文字，来表示自己的想法”。

自主探究与表征，学生会出现几个层次，其中以加减法算式举例居多，集合图与线段图相对少，文字表达的更少，体现了学生具象表达能力占优的特点。让学生自己思考、表征贴近了学生已有的四则运算经验，在后续的交流中，朱老师利用学生的表征图式引导学生进行了抽象和提炼，“从学生中来”的探究素材，使学生的认知经验得到了有效的提升。

2．紧扣“逆”意，搭建框架。

概念教学的一般路径为：建立表象→丰富表象→完善概念。倘若按这样的思路设计教学，通常是这样的流程：学生表征加法→教师补充素材→形成加法概念→加法变式→建构减法概念→教学加减关系。

本课的教学显然又与之不同，框架简洁清晰：学生表征“逆”关系→借助“逆”建构加法与减法概念→利用“逆”关系重构关系网。“逆”关系架起了本课框架，呈现了两个特点：（1）“逆”为载体，能同时呈现加法与减法的概念。（2）“逆”为根源，构成关系网。这样，就将“多”、“散”“乏味”的素材串了起来，其中的关联与意义表达成了学生感觉“神奇”的知识点。

3．厘“逆”之理，实“顺”之基。

“加减关系”存在着千丝万缕的关系，加法是基础，是学生顺向的思维方式，这为学生进一步理解减法和后续学习提供了思维支撑。扎实“加法模型”，将推导出的其他关系式梳理成网，能够帮助学生减轻名称上的记忆负担，进而提高学习的实效。