渗透模型思想 提升核心素养——《解决问题的策略—画线段图》教学设计

颜春红（特级教师）

【教学内容】

苏教版四年级下册第48 页例1、练一练和练习八1～4 题。

【教学过程】

一、引入：创设情境，激活经验

创设情境：每年的3月12日是什么节？（植树节）

师：植树节这天，学校组织学生一起参加了植树活动。

出示两行树实物图，让学生说说哪行多，接着用直条图演示遮盖部分树，让学生猜一猜哪一行树多，为什么？感受同样长的直条表示同样多的数量，再抽象成线段，说说两条线段有怎样的关系？得到：如果用其中的一条线段表示一份，另一条线段表示它的3 倍。

揭示课题：线段图是我们的老朋友了，这节课我们就来研究用画线段图的策略解决实际问题。

【设计意图：创设植树情境，通过出示实物图、半遮盖直条图、直条图让学生再次经历从实物图——半遮盖直条图——直条图——线段图的形成过程，逐步抽象简化了两种事物比较多少的形式，唤醒与激活了学生头脑中对线段图所积累的经验，理解示意图的功能，初步形成线段图的模型，为本节课的学习奠定了基础。】

出示准备题：四年级和五年级共植树72 棵，两个年级植树棵数同样多，两个年级各植树多少棵？

师：这幅线段图能表示两个年级植树棵树间的数量关系吗？

师：谁能口头列式解答？

师：为什么除以2 就能求出每个年级植树的棵数了？

预设：棵数相等。

师：因为两个年级植树棵数相等，所以只要用72÷2＝36（棵）。这道题数量关系非常清晰，我们很快就解决了问题。

【设计意图：在本节课学习之前，学生已经具备画线段图分析与解决问题的经验，让学生在读准备题以后，给出线段图让学生将图与文字对应起来，解释图的意思，感受到线段图在表达数量关系中的优越性，同时也为例题的教学做好准备。】

二、展开：探究讨论，构建模型

出示例1（改口答题为例1）：四年级和五年级共植树72 棵树，五年级比四年级多植12 棵。两个年级各植树多少棵？

1.审题。

师：谁来读一读？

师：题目中告诉我们哪几个条件？求什么问题？

预设：有两个条件，是……，问题是……

师：通过读题我们弄懂了题目的意思，看来在解决问题时读题审题这一步骤不能马虎！

师：还能口答这道题吗？

生：不能。

师：比一比这两道题，有什么不同？

预设：虽然只变化了一个条件，但数量关系复杂多了。

师：那有什么好的方法可以将数量关系清楚地表示出来呢？

预设：可以画线段图解决。

2.画图。

师：想一想，应该怎么画图？独立思考后，在学习单上试着画一画。

（展示学生画的图，逐步完善，得到完整的图）

【设计意图：四年级的学生已经积累了丰富的画图经验，完全有能力独立画出线段图。只是学生在画线段图的过程中由于个人经验不同、学习水平与能力也有所不同，所画的线段图有可能不规范不完整，通过对不同学生所画的线段图的展示与评价，让学生理解一幅完整的线段图所具有的要素，并对自己所画的线段图进行完善，得到规范完整的线段图，将文字表达的实际问题，通过线段图模型进行了简化，使数量关系变得直观易于理解。】

3.看图分析数量关系。

师：接下来，请大家仔细看线段图，分析数量关系，想一想，解决这道题的关键是什么？

预设：上一道题之所以简单，是因为四、五年级植树棵数相等，如果将这道题的四、五年级棵数变成相等的，解决起来就非常容易了！

师：如何能让四、五年级植树棵数相等？你有哪些好方法？想到的就和你的同桌说一说，并在《学习单》上写出解题过程，如果没有思路，可以看屏幕（二年级让两数相等的三种方法例题图），是否能给你一些启发？

过渡：老师已经看到不少同学列出算式解答完毕，下面就结合图来分享一下你的想法。

预设一：把五年级多植的12棵减去，总数就减去12 棵，这时等于四年级植树棵数的2 倍，先算出四年级的植树棵数。

预设二：把四年级增加12棵，总数就加上12 棵，这时等于五年级植树棵数的2 倍，先算五年级的植树棵数。

预设三：先把五年级多植的12 棵平均分成2 份，给四年级6棵，这样两个年级就一样多，都是72 除以2 得36 棵，36 减6 得30棵是四年级植树的棵数，36 加6得42 棵是五年级植树的棵数。

师：通过画线段图分析数量关系我们找到了三种解题思路，虽然思路不同，本质上却是一样的，都是先想办法让两个年级植树棵数相等，这正是解决这道题的关键。

【设计意图：让学生根据线段图分析数量关系，说一说解决这道题的关键是什么？如果学生无法回答，让学生比较准备题和例题，讨论得出解决问题的关键是将四、五年级植树棵数变相等。再结合二年级上学期将花片变相等的三种方法教材图，说说如何将四、五年级植树棵数变相等。解决这道题有三种思路，虽然思路不同，本质却是相同的，都是将不相等的两种数量变相等再解决。通过比较，让学生抓住解决问题的关键，感悟数学的本质。】

4.比较不同情境，抽象数学模型。

师：请同学们打开数学书第48 页，根据题意把线段图补充完整，再列式解答。

师：书上这道题与屏幕上的这道题有哪些相同和不同？

预设：数相同、线段图相同、解题思路相同，不同的只是一个是植树问题，一个是邮票问题。

师：也就是说除了解决的是植树问题和邮票问题不同外，其他都是相同的。根据这样的数量关系，你还能想到解决什么问题？你能将数据也换了吗？

【设计意图：教学中要注重让学生经历从特殊走向一般的归纳推理过程，通过抽象数学模型，帮助学生建构数学概念的意义，真正理解新学知识的内涵与本质。因此这个环节我设计了比较植树问题与教材例题中的邮票问题的相同点和不同点这个活动，通过比较，舍弃了具体问题情境，发现两个问题之间的本质联系，再通过举大量的实例使学生真正理解和差问题的数量关系，抽象出和差问题的数量关系模型。】

5.检验作答。

师：要想检验求得的结果是否正确可以怎么办？

师：我们可以“把得数代入原题”进行检验，42+30＝72（棵）42－30＝12（棵），与题目中所给的条件完全相符，所以我们再次肯定答题正确。

6.回顾反思。

师：回顾一下解决问题的过程，你有什么想说的吗？画线段图分析数量关系有什么好处？

（板书：清楚、直观，便于分析）

三、总结：运用模型，循环提升

1.出示线段图。

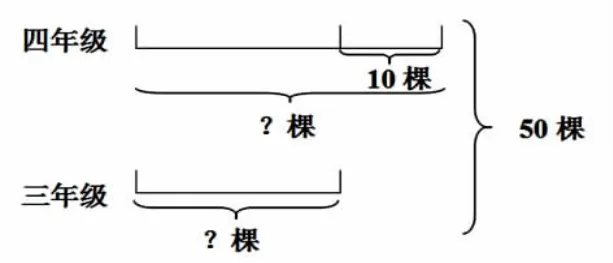
让学生根据图意说说条件和问题。口头列式，课件呈现算式。

将一、二年级植树线段在原有线段图下面出示，问学生：一、二年级植树多少棵？你怎么知道的？那你知道现在一共植树多少棵吗？（将50 棵改成90 棵）如果不知道一、二、三年级的植树棵数，根据线段图可以怎么列式？

2.挑战想像力。

（1）一个双层书架，上层书的本数是下层的3 倍。

师：根据这个条件，能在头脑里想像出线段图的样子吗？（学生想象后呈现线段图）和你想的一样吗？

（2）出示：上层书比下层书多120 本。

师：这个条件怎样在图中表示？（让学生用手比划再呈现图）说说和你画的一样吗?

学生口答：上、下层各有多少本书。

3.练习第4 题。

一个双层书架，上层书的本数是下层的3 倍。如果从上层搬60 本书到下层，那么两层书的本数正好相等。原来上、下层各有图书多少本？

师：你能看着线段图告诉大家怎么搬吗？

说明：题目要求是从上层搬到下层60 本，上、下层本数相等，看图就能发现从上层搬三份中的一份到下层，上、下层的本数相同，所以这一份就是60 本。

5.练习第5 题。（机动）

一个双层书架上共放了72本书，上层书的本数比下层的3倍多12 本。上、下层各有图书多少本？

师：复杂多了，怎么办呢？（生：画线段图。）和老师想到一起去了（PPT 呈现）。

师：有了线段图，更清楚直观！分析线段图，想想怎样解答！

【设计意图：运用数学模型去解决现实生活中的问题，学生要学会把错综复杂的实际问题充分简化和抽象为合理的数学结构，要学会抓住问题的主要矛盾，寻找和发现反映实际问题的数量关系。习题的设计采用由浅入深、逐步拓展的方法，使学生在解决问题的过程中不仅沟通了问题之间的联系、抓住了问题的本质，也使学生真正将数学模型的构建作为自主行为，积极主动地参与数学问题的解决过程中。】

四、课堂总结

师：今天我们重点研究了解决问题的哪种策略？（画线段图）线段图帮助我们解决了这么多复杂的问题，你不想对这个老朋友说点啥？画线段图分析的确是一种有效的解决问题的策略，同学们以后要学着用好它！

【设计意图：本节课基于整体视角，让学生充分经历了经验唤醒、问题提出、直观操作、分析推理、比较抽象、应用拓展的数学建模全过程，帮助学生构造数学模型，体会数学知识内在关联，理解数学本质，灵活用数学模型去描述与刻画现实世界，在探究讨论活动中促进学生对数学知识与数学意义的建构，真正提升学生的数学核心素养。】