振弦式陀螺电磁驱动结构设计与电磁分析
2020-04-15陈志龙于庆奎
陈志龙,刘 鹏,舒 凯,黄 鸣,于庆奎
(1. 南昌理工学院, 南昌 330044;2. 华东交通大学机电与车辆工程学院, 南昌 330013;3. 中国航天宇航元器件工程中心, 北京 100094)
0 引 言
振动式陀螺是应用微机械加工技术与微电子工艺技术制作的一种惯性传感器[1],它具有体积小、重量轻、功耗低、易于集成等特点,在车辆驱动防滑控制系统、数码摄像机防抖动控制系统、机器人姿态感知与控制系统、平台稳定系统、炮弹制导等领域得到了广泛的应用[2-3]。振动式陀螺是通过高频振动的质量在被基座带动旋转时所产生的哥氏效应来敏感角运动,振弦式传感器是通过检测振弦上频率的改变量来敏感外力,而振弦式陀螺是把振动式陀螺的工作机理与振弦式传感器的测量机理相结合的一种陀螺。
驱动系统是振动式陀螺重要组成部分,它的主要功能是使敏感部件产生高频振动,振动陀螺的驱动方式主要是运用场力来驱动,如静电力、电磁力等。文献[4-8]报道的振动陀螺都是采用静电驱动,虽然静电驱动具有功耗低的特点,但工作电压高与目前片上常用的工作电压(小于5 V)不兼容,难以适应系统集成与微电子器件的发展趋势[9]。早在1998年文献[10]就报道一种基于电磁驱动原理的硅片摆角速度传感器,驱动时可获得高达50 μm的振动幅值,芯片在常压、100 Hz带宽下,能获得0.3 (°)/s的分辨率。文献[11]提出了一种环状振动微陀螺,工作方式为电磁驱动,其中需要安装一个永磁体,其偏置稳定性达到0.6 (°)/h。文献[12]提出了一款内外环具有独立线圈的电磁驱动振动陀螺,在平行磁场中,通过线圈对内环施加磁场力,平行磁场方向与扭杆呈45°夹角,灵敏度达0.87 mV/((°)· s-1)。文献[13]利用了电流驱动线圈和永磁铁之间的作用力设计了一种电磁驱动装置,该装置实现了可控刚度作为参数刚度激励装置的数值模拟。文献[14]在电磁场激励下,研究了永磁驱动器,建立了励磁电流与永久磁铁的理论模型,并进行了实验验证,结果表明可以获得更好的驱动力。近年来随着高深宽比微结构加工的半导体工艺、设备的发展,原先困扰电磁驱动研究的加工手段问题已不再突出,电磁驱动具有工作电压低且具有响应速度快、驱动力较大、适用范围广等优点,并且电源相对容易提供[15-16]。
本文依据振弦式陀螺工作原理提出一种电磁驱动方案,采用平面线圈与对称磁体组合的驱动装置驱动振弦式陀螺。振弦式陀螺采用电磁驱动、频率检测的工作方式,获得了较大的驱动力、较高的频率分辨率和控制精度,具有结构简单,容易实现的优点。
1 振弦式陀螺的工作原理与电磁驱动模型
1.1 振弦式陀螺的工作原理
图1为振弦式陀螺的简化模型。质量块m固连在旋转坐标系的xy平面内,模型具有2个振动模式,每个模型都简化为弹簧-阻尼-质量模型。假定质量块在y方向受到某种激励作用而受迫振动,而z轴有角速度Ω输入时,质量块在x方向就会受到交变的哥氏力作用而沿x轴方向产生诱发振动,从而可通过振弦的频率检测,测出角速度输入量。
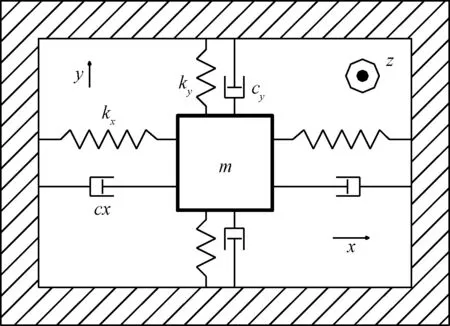
图1 振弦式陀螺的简化模型Fig.1 Simplified model of vibrating string gyro
1.2 振弦式陀螺电磁驱动电学模型
振弦式陀螺电磁驱动是基于安培力设计的一种驱动方式:位于均匀磁场中的通电线圈切割磁感线产生安培力,并通过安培力作用带动框架进行直线往复运动。要建立电磁驱动的电学模型首先需要对电磁驱动电力系统进行简化,图2所示为经过简化后的电磁驱动等效图。
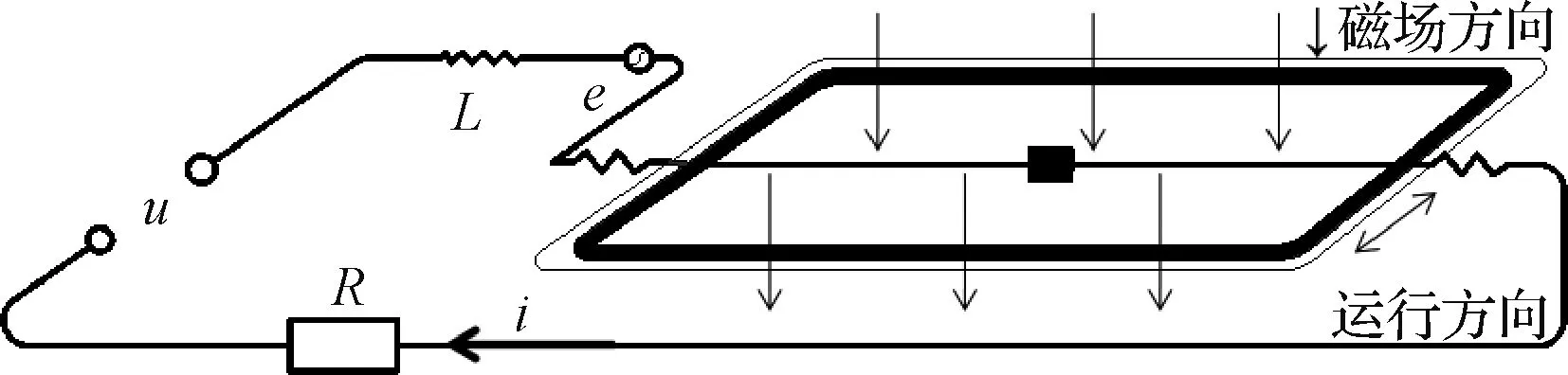
图2 电磁驱动电路简化模型Fig.2 Simplified model of electromagnetic drive circuit
按图2所示,线圈框架外部驱动电压为u,线圈的等效电感及等效电阻分别为L,R,电流i在磁场中产生的感生电动势为e。由电路的基尔霍夫第二定律可得到上述模型电压动态平衡方程:
(1)
e=δBlv
(2)
(3)
1.3 振弦式陀螺电磁驱动动力学模型
对电磁驱动电学结构进行分析,永磁体与线圈框架之间要产生相对运动,首先需要电磁力FV能够克服框架运动的阻尼力FC。在实际应用中,框架通常需要完成加减速运动,此时要求电磁力FV能够克服框架产生的惯性力FM。框架还需承受弹簧支撑阻力Fk。从而可以得到电磁驱动动力学平衡方程式如下:
(4)
2 振弦式陀螺的电磁驱动结构设计与电磁仿真分析
2.1 电磁驱动整体结构设计
振弦式陀螺采用电磁驱动、频率检测的工作方式,电磁驱动能够获得较大的驱动力,并且结构简单,容易实现[17]。电磁驱动作为振弦式陀螺的主要部件,线性良好的电磁驱动结构有利于提高振弦式陀螺的性能,简化控制难度。振弦式陀螺电磁驱动初步结构模型如图3所示。它是由一对背轭架为支撑的对杆磁铁和一个带有支架的线圈框架组成的,线圈框架位于永磁体边界内,获得均匀的磁感应强度。
利用铝合金等有色金属材料作为线圈框架的支架,可以避免磁滞、涡流损耗以及铁磁材料的非线性特性影响[18]。树脂材料可以作为磁场通道的轭架,磁场的相对磁导率可以达到几百甚至更多;线圈采用并联布线,以此来减少线圈的总电阻值。永磁体和线圈框架的尺寸参数如图4所示。α,γ,δ分别为永磁体的长度、厚度、宽度。Ν,Η,Κ分别为线圈框架厚度、宽度、长度。电磁驱动的力、线圈框架的重量和总散热都取决于结构的尺寸,线圈框架所在气隙中的磁感应强度受磁铁尺寸和轭架结构的影响。
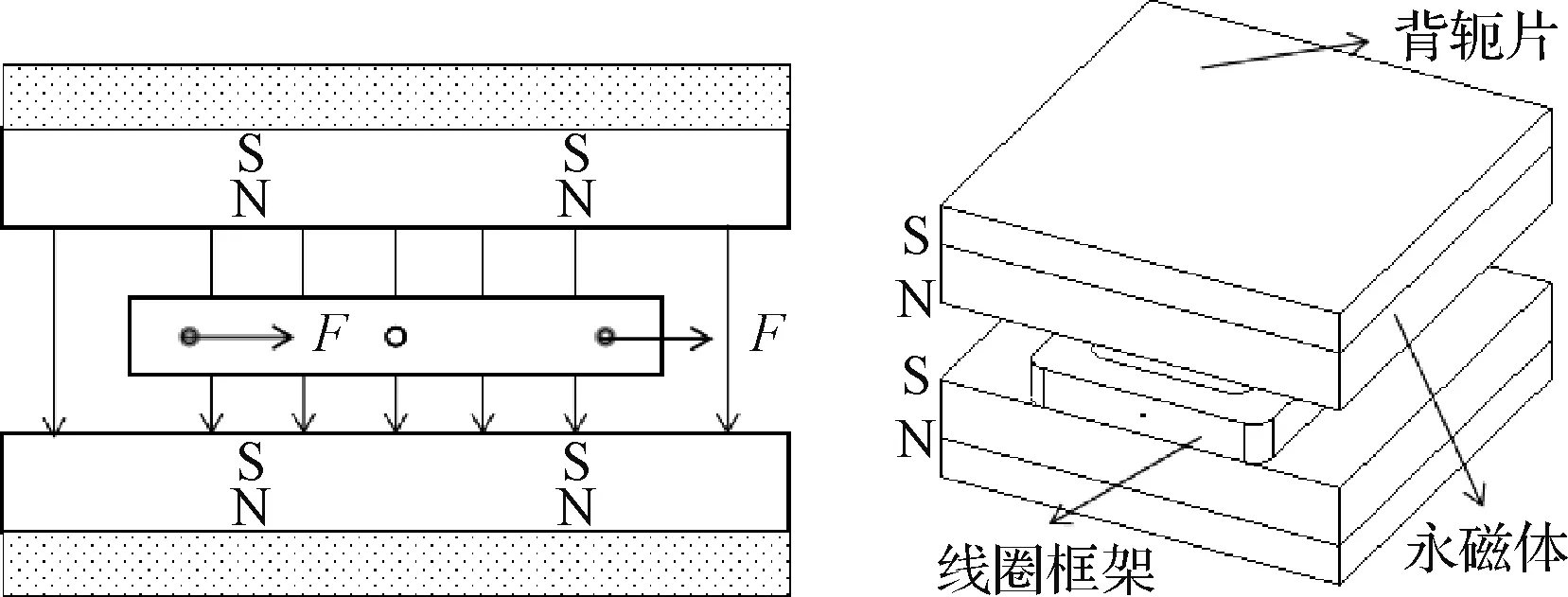
图3 电磁驱动结构设计示意图Fig.3 Schematic diagram of electromagnetic drive structure design
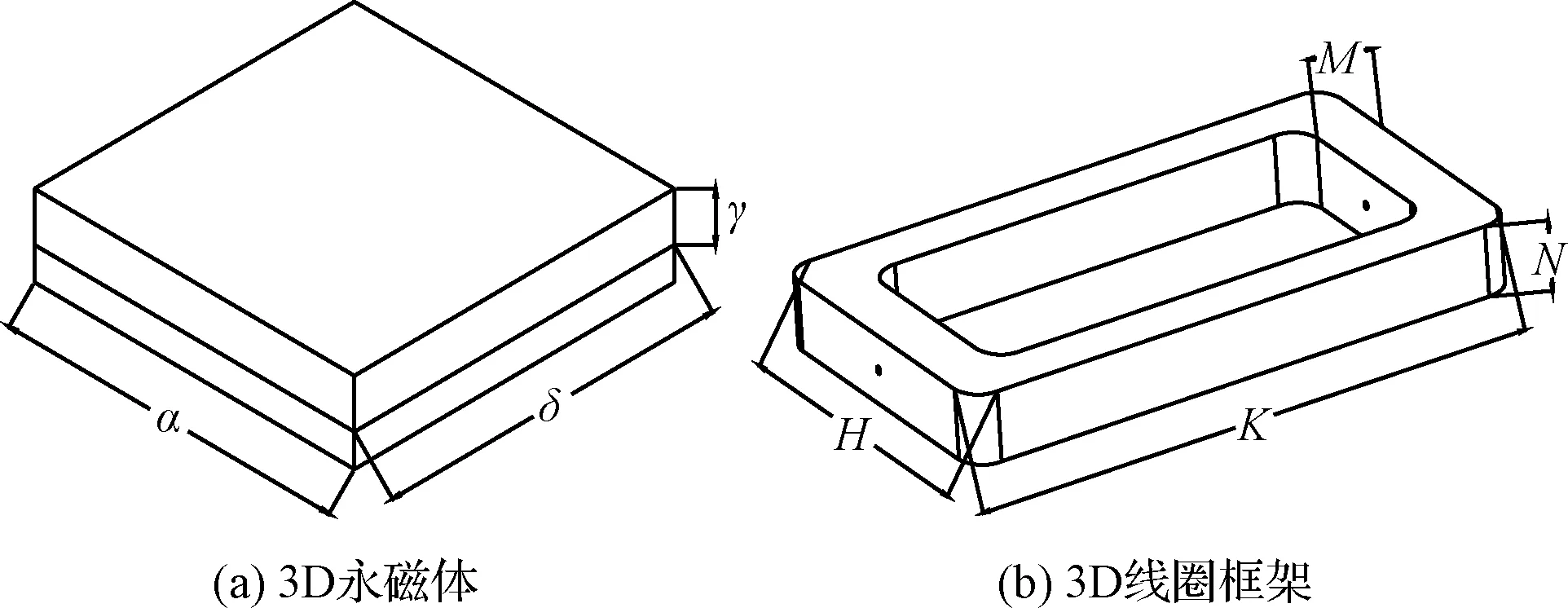
图4 永磁体和线圈框架的尺寸参数示意图Fig.4 Schematic diagram of size parameters of permanent magnet and coil frame
永磁体和线圈框架的相对位置如图5所示,其中h,y,e是电磁驱动机构的最大尺寸,f是线圈框架的最大单边运动行程,p和q是线圈框架内圈的基本尺寸。永磁体材料的性能对电磁驱动系统具有重要作用,铷铁硼永磁体具有较高的矫顽性和剩磁性,在高温下稳定性能好,既能增加磁力,又能降低消磁效果。初选N38H作为永磁体材料,其剩磁率为1.24 T。根据振弦式陀螺的工作原理,当电磁驱动工作时,间隙距离应足够大,以避免线圈框架在响应时间内与永磁体碰撞,因此,间隙距离应大于最大振幅和线圈厚度的两倍。假设线圈总厚度为c,间隙距离与线圈框架厚度的关系可以表示为s≥N+2b+c,根据磁通量密度方程,由于振弦式陀螺的模型是对称的,所以永磁体与永磁体之间的相对位置关系是对称的,该线圈框架是由以下条件设计的,即δ≥2M+P+2f,K≤δ。
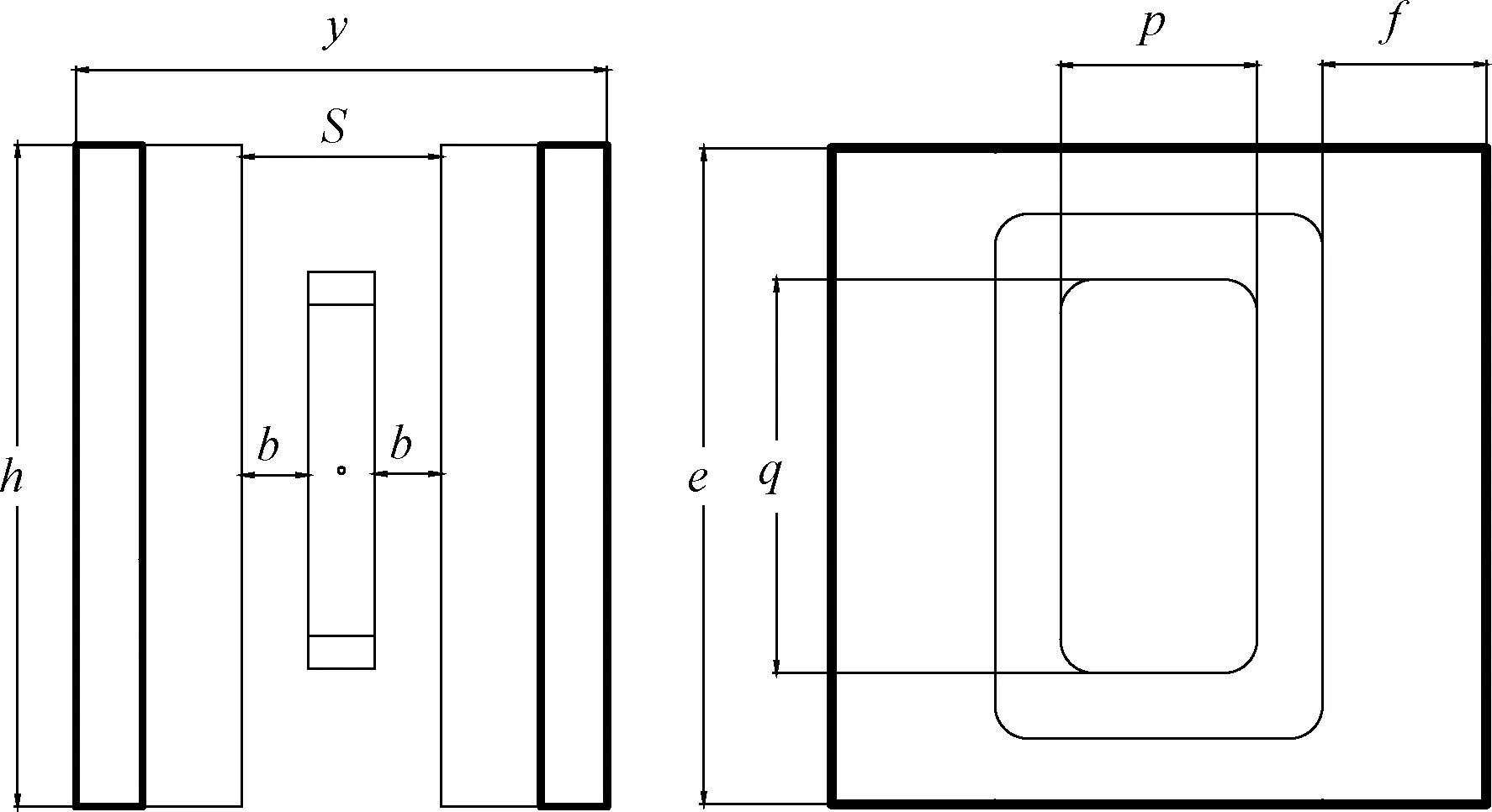
图5 永磁体和线圈框架的相对位置示意图Fig.5 Schematic diagram of the relative position of the permanent magnet and the coil frame
安培力可以表示为:
F=2NcBsIK
(5)
式中:Nc为线圈的总匝数。
因为间隙距离是S,线圈框架的最大单边间隙是b,铜线的厚度为dc,各层厚度可以写成L:
(6)
线圈的重量Mc:
Mc=ρηpackVc
(7)
式中:ρ为铜线密度,Vc线圈的体积,ηpack是线圈的填充系数。
热耗散为Q:
(8)
根据安培力方程,利用MATLAB软件设计目标和初始参数计算[18],可以初步得到永磁体与线圈之间的相对位置关系、线圈框架的尺寸、安培力、线圈重量和散热。假设电磁驱动初始需要5 N安培力,根据设计方案,电磁驱动机构初始参数如表1所示。

表1 电磁驱动机构初始参数Table 1 Initial parameters of electromagnetic drive mechanism
2.2 振弦式陀螺电磁驱动电磁分析
通过ANSYS Maxwell电磁分析软件对振弦式陀螺电磁驱动结构的磁路进行仿真分析,得到永磁体的磁力线分布与磁路走向,在线圈的工作区域内形成了一个相对均匀的磁场,永磁体边界内的磁感应强度几乎是恒定的,一旦线圈超过边界,磁通就会大大减小。在振弦式陀螺中,框架的驱动力则以运动方向的电磁力大小为衡量。框架的驱动力由式(9)和式(10)决定:
(9)
F=-∮B×Idn
(10)
其中,
I=JdS
式中:永磁体的极化强度为M,线圈框架中的电流密度为J,其大小是用流过线圈横截面的总电流与横截面积的比值表示,方向是沿着电流方向。式(10)计算永磁体在空中某一点的磁感应强度大小,式(11)则计算通电线圈在永磁体所产生的磁场中的受力。
从式(11)可以看出,通电电流和磁感应强度是影响振弦式陀螺线圈框架受力的主要因素,现主要分析线圈框架在平衡位置时,永磁体在陀螺纵向范围内气隙磁感应强度的变化情况,如图6所示,永磁体边线位置为零点,向下为正方向;以及永磁体在陀螺横向范围内气隙磁感应强度的变化情况,如图6所示,中间位置为起始零点,向右为正方向。在电流一定的情况下,振弦式陀螺线圈框架驱动力的大小是由永磁体在陀螺气隙中所形成的磁感应强度决定,因此仅考虑线圈通电电流一定的情况下,气隙处的磁感应强度分布情况,此外忽略重力场因素的影响。为了得到相对较大的磁感应强度,选择剩磁和矫顽力较大的型号的永磁体,综合磁特性性能和经济效应,选择型号为N38H的NdFeB材料,剩磁为1.24 T,矫顽力为880 kA/m,选择通电电流为10 mA。
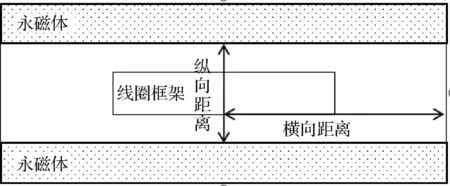
图6 电磁驱动分析横向与纵向范围示意图Fig.6 Schematic diagram of transverse and longitudinal range of electromagnetic drive analysis
2.2.1永磁体尺寸对气隙磁感应强度的影响
在对永磁体宽度进行仿真分析时仿真条件为:永磁体极化强度M=1.24 T,矫顽力为880 kA/m,厚度为5 mm,永磁体间隙为5 mm;背磁片为铁片DT4C,磁导率μ=0.02 H/m;设计背磁片与永磁体尺寸相同,考虑振弦式陀螺尺寸匹配问题,选择宽度尺寸为45 mm、50 mm、55 mm、60 mm进行分析。
从图7(a)可以看出,不同宽度尺寸的永磁体产生的磁感应强度是比较均匀的,增加永磁体尺寸后,气隙处的磁感应强度略微减小;减小永磁体宽度尺寸后,气隙处的纵向磁感应强度反而增大,且增大的幅度也呈增大的趋势。从图7(b)可以看出,线圈框架在有效行程内磁感应强度比较均匀,宽度尺寸相对较小,则磁感应强度略微大些,在线圈框架行程的两极端具有气隙磁感应强度突增的现象,这种现象来源于磁场的泄漏,在振弦式陀螺外框架设计时,要考虑磁场屏蔽,防止驱动框架磁场外漏。在此分析条件下永磁体宽度尺寸具有尺寸相对越小,磁感应强度越强的优点。因此在设计振弦式陀螺电磁驱动时,应尽量选取宽度尺寸较小且符合陀螺框架尺寸的永磁体。
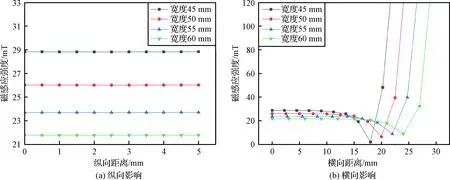
图7 永磁体宽度对气隙磁感应强度的影响Fig.7 Effect of permanent magnet width on air gap magnetic induction intensity
在对永磁体厚度进行仿真分析时仿真条件为:磁体极化强度大小M=1.24 T,矫顽力为880 kA/m,永磁体宽度为30 mm,永磁体间隙为5 mm;背磁片为铁片DT4C,磁导率μ=0.02 H/m。考虑振弦式陀螺总体尺寸与重量因素,永磁体厚度尺寸取3 mm、5 mm、8 mm、10 mm。
从图8(a)可以看出,纵向磁感应强度分布相对均匀,当增大永磁体厚度后,气隙处的纵向磁感应强度相对增大,但增大的幅度也呈减小的趋势。从图8(b)可以看出,线圈框架在有效行程内磁感应强度比较均匀,厚度尺寸相对较厚,则磁感应强度较大。
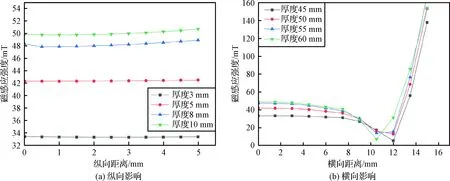
图8 永磁体厚度对气隙磁感应强度的影响Fig.8 Effect of permanent magnet thickness on air gap magnetic induction intensity
2.2.2永磁体间距对气隙磁感应强度的影响
在进行永磁体间距仿真分析时仿真条件为:磁体极化强度大小M=1.24 T,矫顽力为880 kA/m,厚度为5 mm,永磁体宽度为30 mm;背磁片为铁片DT4C,磁导率μ=0.02 H/m,保持其余参数均不变,仅改变永磁体间距的参数。考虑线圈框架实际尺寸,实验分析间距选择3 mm、5 mm、8 mm、10 mm。由图9(a)可知,增加永磁体间距后,气隙处的纵向磁感应强度减小,但过小的永磁体间距,会影响气隙中所形成的磁感应强度,达不到磁感应强度增大的效果,当间隙一定时,气隙处的纵向磁感应强度处于稳态,在一小范围内波动。由图9(b)可知,线圈框架在有效行程内磁感应强度比较均匀,但相对永磁体间隙越大,磁感应强度越低,且有磁漏现象。
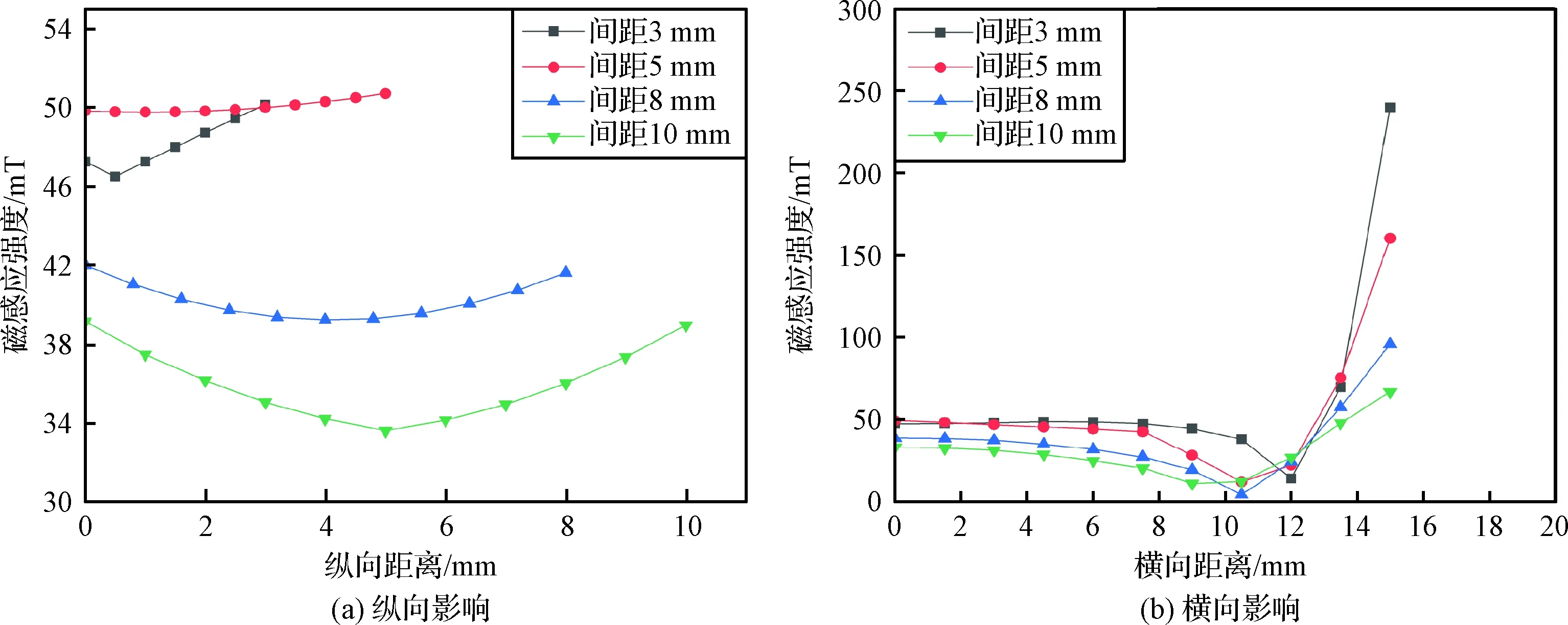
图9 永磁体间距对气隙磁感应强度的影响Fig.9 Effect of permanent magnet spacing on air gap magnetic induction intensity
2.2.3背磁片对气隙磁感应强度的影响
振弦式陀螺电磁驱动中永磁体的磁力线是一个闭环线,一定磁感应强度的永磁体的总磁通量是固定不变的,而背磁片的作用是可以用磁路设计的方法来聚集磁通以增强磁感应强度,主要在于聚集磁力线,防止驱动框架磁场纵向外漏。由图10可知,在气隙处的纵向气隙磁感应强度和横向气隙磁感应强度,有背磁片处的磁力线聚集效果很好,磁感应强度得到较大提高。
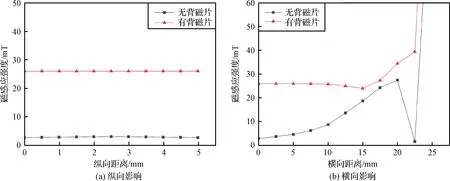
图10 背磁片对气隙磁感应强度的影响Fig.10 Effect of back iron on air gap magnetic induction intensity
永磁体磁路的聚集效果越好,则气隙侧的磁感应强度就越大,一般会使用厚度较厚的背磁片来聚集磁路,但是由于总磁通是不变的,所以背磁片厚度达到一定值时,再增加厚度,气隙侧的磁感应强度是不会再增加。在设计磁屏蔽时,一般用纯铁片DT4C作为背磁片来实现磁力线引导与屏蔽效果,在对背磁片厚度进行仿真分析时,考虑背磁片材料的选取与加工,背磁片厚度尺寸取1 mm、2 mm、3 mm。从图11可以看出,纵向磁感应强度分布相对均匀,且不同厚度的背磁片对气隙磁感应强度影响不是很大,横向磁感应强度值几乎重合,所取背磁片厚度对磁力线聚集效果一样,在考虑振弦式陀螺驱动设计时,宜选取较薄的背磁片。
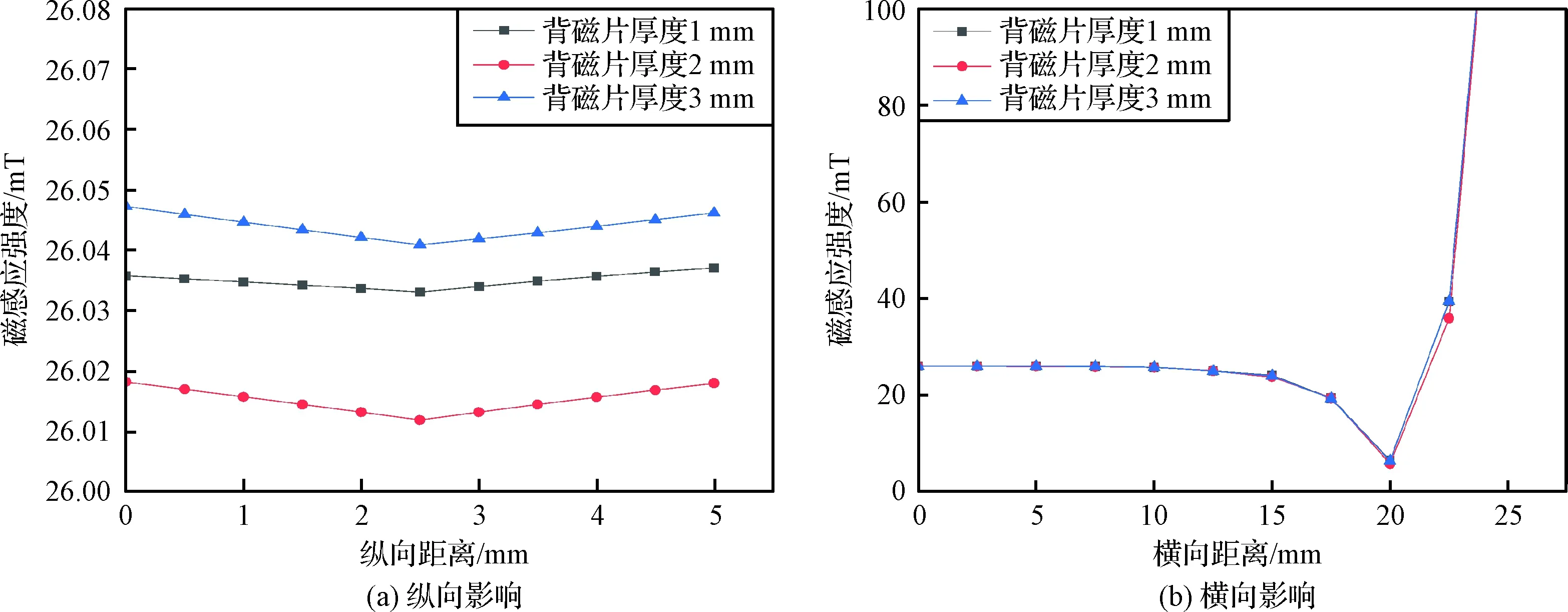
图11 背磁片厚度对气隙磁感应强度的影响Fig.11 The influence of thickness of back iron plate on air gap magnetic induction intensity
2.2.4Halbach永磁体排列对气隙磁感应强度的影响
在进行永磁体阵列设计时,为了使线圈框架获得有效的驱动力从而能很好的实现运动,永磁体需要满足外漏磁场较小,线圈框架所处的空间磁场较为均匀且磁场强度较大等要求。Halbach永磁阵列是一种新型永磁体排列方式,该阵列由若干块磁化强度相同的永磁体组成,相邻两块永磁体间磁化方向相差一个固定角度,由此可使得永磁体一侧磁场强度得到强化。
在对Halbach永磁阵列仿真分析时仿真条件为:磁体极化强度大小M=1.24 T,矫顽力为880 kA/m,厚度为5 mm,永磁体间隙为5 mm;背磁片为铁片DT4C,磁导率μ=0.02 H/m,选择单体永磁体与Halbach永磁体阵列进行气隙磁感应强度比较。从图12可以看出,Halbach永磁体阵列纵向磁感应强度在行程内最小值远大于单体永磁体磁感应强度,当采用Halbach永磁体阵列时,气隙处的纵向磁感应强度相对增大;而Halbach永磁体阵列横向磁感应强度在行程中间位置会出现波峰值,且整体气隙磁感应强度远大于单体永磁体磁感应强度,波峰位置刚好与线圈框架电流处相重合,对线圈框架产生较强的气隙磁感应强度。
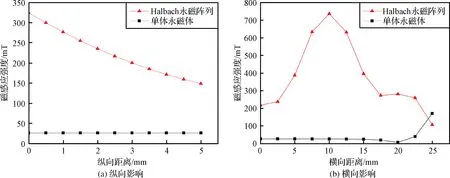
图12 Halbach永磁阵列排列对气隙磁感应强度的影响Fig.12 Effect of Halbach permanent magnet array arrangement on air gap magnetic induction intensity
3 振弦式陀螺电磁驱动整体结构仿真分析
为了验证设计的振弦式陀螺电磁驱动结构的可行性,通过ANSYS Maxwell的电磁分析模块建立振弦式陀螺电磁驱动整体结构二维仿真模型(见图13),并进行电磁驱动整体结构模型仿真;为了提高建模与运算的简便快捷性,将电磁驱动整体三维结构简化成二维平面问题,考虑其截面为轴对称图形,选择智能网格划分以及四边形网格结构单元,施加无磁漏的磁力线平行边界,并在线圈单元施加电流密度输入励磁载荷。如图14所示,仿真结果表明,电磁驱动整体结构模型气隙磁感应强度得到很大提高,纵向磁感应强度波动范围小,横向磁感应强度出现平稳波峰,有利于线圈框架设计时的位置调节;在电流一定的情况下,可以很好的提高陀螺框架驱动力,有利于优化陀螺结构尺寸,降低陀螺功耗,验证了振弦式陀螺电磁驱动方案模型的可行性。
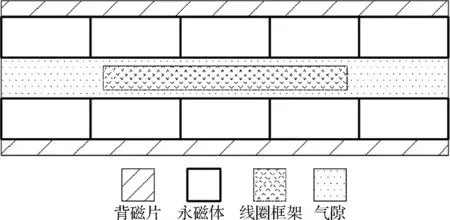
图13 电磁驱动结构二维仿真实体模型Fig.13 Electromagnetic drive structure two-dimensional simulation entity mode
4 结束语
振弦式陀螺电磁驱动方式采用了永磁体加电流的方案,利用电磁场中的安培力驱动线圈框架运动。本文从对振弦式陀螺电磁驱动设计方案进行推导计算和仿真,得出振弦式陀螺电磁驱动系统主要受永磁体尺寸、永磁体间距、背磁片、永磁体阵列等因素的影响,合理地选择这些参数可以有效提高电磁驱动性能。永磁体宽度具有尺寸相对越小,磁感应强度越强,而当增大永磁体厚度后,气隙处的纵向磁感应强度相对增大,但增大的幅度也呈减小的趋势;永磁体间隙越大,磁感应强度越低,且带有磁漏现象;背磁片的使用会对磁力线聚集产生很好的效果,Halbach永磁阵列对磁力线单边聚集具有很好的效果,且对线圈框架产生了较强的气隙磁感应强度。综合考虑振弦式陀螺电磁驱动影响因素,优化设计振弦式陀螺结构模型并进行振弦式陀螺电磁驱动结构模型仿真分析。结果表明,电磁驱动结构模型气隙磁感应强度得到倍增,验证了振弦式陀螺电磁驱动方案模型的可行性,研究结果为后续振弦式陀螺的结构优化设计与实际产品试制研究奠定了理论基础。
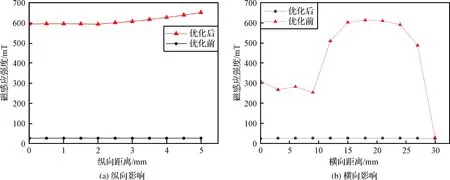
图14 振弦式陀螺电磁驱动结构模型气隙磁感应强度Fig.14 Model of vibrating string gyro electromagnetic drive structure: air gap magnetic induction intensity
