高超声速飞行器的抗饱和切换控制

刘田禾，安 昊，王常虹

(哈尔滨工业大学空间控制与惯性技术研究中心，哈尔滨150001)

0 引 言

高超声速飞行器主要指飞行速度马赫数在5以上的飞行器。该类飞行器具有飞行速度快、飞行空域广、作战距离长等特点，自问世以来就得到了各个航空航天大国的重视[1]。随着电子技术、超燃冲压发动机、复合材料学等高新科技相继取得重大突破，高超声速飞行器的制导控制、气动布局、热防护等关键技术的研究也有了长足的进展[2]。根据所使用的动力系统不同，高超声速飞行器主要分为火箭助推式和吸气式。其中，吸气式高超声速飞行器主要依靠超燃冲压发动机作为动力，具有结构简单、维护方便、有效载荷高等优点，是目前国内外的研究重点[3]。

高超声速飞行器的动力学特性带有的强非线性、飞行器模型中存在的不确定参数以及飞行过程中需要满足苛刻的工作条件均为高超声速飞行器控制带来了非常大的挑战[4-5]。众多研究人员致力于研究高超声速飞行器的建模及控制问题，并尝试了包括反步法[6-7]、自适应控制[8]、滑模变结构控制[9-10]、模糊控制[11-12]等众多控制方法。在诸多控制方法当中，反馈线性化由于先期研究成果较为丰富、设计流程简单而受到众多学者的青睐[13-15]。然而，由于一般的反馈线性化控制方法需要满足线性化条件，使得高超声速飞行器在进行大幅度机动时容易造成模型失真，且使用Lie导数求取需要大量的运算，难以保证系统实时性，使得实际工程上难以直接实现。切换系统通过在多个子系统模型之间进行切换的方式为复杂动态系统的控制问题提供了简单而有效的解决方案。本文提出一种基于切换系统的高超声速飞行器建模方法。通过将高超声速飞行器的飞行包线进行分区，为各个区域建立独立的系统模型，使得飞行器在单个区域内机动时的模型参数变化可以忽略。当飞行器需要进行大范围机动时，可通过在不同区域之间切换的方式，自主选取对应的系统模型，降低模型失真所带来的影响。

在建立高超声速飞行器切换系统模型基础上，为了进一步提升飞行控制器性能，可为不同的子系统单独设计控制器。其优势在于可以进一步细化各控制器对应的飞行空域，提升控制效率。然而，在系统模态进行切换时，可能会遇到信号传输时滞等问题，使得控制器的切换滞后于系统模态的切换，通常称这种现象为异步切换。异步切换会使得本应单调递减的Lyapunov函数出现上升的可能，进而影响切换系统的稳定性。因此，在设计切换控制器时，还有必要将异步切换的影响纳入考虑。此外，切换信号的选择同样是切换系统控制的一部分。通过适当地选择切换信号，能够对子系统模态的切换进行正确的描述，有助于控制器的设计以及系统稳定性的保障。驻留时间信号(Dwell time, DT)和平均驻留时间信号(Average dwell-time,ADT)作为两类常见的切换信号而受到众多学者的广泛关注，也在众多工程问题上得到了应用[16-18]。然而，对于具有复杂动态模型的高超声速飞行器而言，尽管DT和ADT信号能够对多数情况下的飞行器飞行状态进行描述，但在飞行器进行复杂机动等极端情况下，飞行器的系统模态切换频率可能会超出该类切换信号所允许的极限。为了更精确地对高超声速飞行器的飞行过程进行描述，并确保控制器能够始终保持有效，本文所考虑的切换信号为持续驻留时间(Persistent dwell-time,PDT)信号。该类切换信号由子系统模态不可切换的τ部和子系统模态可任意切换的T部构成。通过适当调整两者的长度，PDT可涵盖包括DT、ADT、随机切换等多种切换信号。因此PDT具有更强的一般性及对快速切换的描述能力。然而，由于PDT信号较为复杂，目前对该类信号的研究相对较少[19]。

另一方面，高超声速飞行器由于自身物理特性的限制使得执行机构输出幅值不能无限增大，在执行飞行任务中可能会受到执行器饱和的影响[20]。例如，超燃冲压发动机燃流量存在限制；鸭翼、升降舵等偏角无法任意转动等。因此，在设计控制器的同时还需要考虑执行器饱和的问题，以避免由于控制器的控制量与被控对象的执行程度不匹配而造成系统性能退化甚至不稳定[21]。目前，对饱和非线性的处理方法主要分为两种：单步法和两步法。其中，单步法的特点在于不回避饱和环节，根据系统性能需求从底层设计控制器。尽管单步法从原理上可行，但存在着一些问题：1)在线性区域内(即执行器未发生饱和时)，系统性能会受到一定影响；2)在一些带有约束的系统中，该方法的控制器保守性较高，缺乏实用性[22]。相对而言，两步法的思路更为直观：首先不考虑饱和约束，直接为系统设计控制器，然后通过加入抗饱和补偿器处理饱和约束。本文针对高超声速飞行器的切换系统模型，以线性矩阵不等式的形式给出了一类抗饱和切换控制器的设计方法，使得受到饱和非线性约束的切换系统能够在特定切换信号的作用下保持全局一致渐近稳定性。

本文主要研究了高超声速飞行器的抗饱和切换控制问题。首先使用Jacobin矩阵的方式，将高超声速飞行器模型线性化，并将飞行包线分区以建立切换系统模型。在该模型的基础上，为高超声速飞行器设计了抗饱和切换控制器。

1 高超声速飞行器的面向控制的切换系统模型

1.1 高超声速飞行器的刚体动力学模型

吸气式高超声速飞行器的动力学模型非常复杂。本文采用目前较为常见的高超声速飞行器纵向动力学模型[23-24]，其具体表达式如下

(1)

式中：V为飞行器速度；h为飞行高度；α,θ和Q分别为攻角、俯仰角和俯仰角速率；T,D和L分别是推力、阻力和升力；Myy为俯仰力矩；Iyy为俯仰转动惯量；m和g为质量和重力加速度。

式(1)中的推力、阻力、升力和俯仰力矩可通过下式进行拟合

(2)

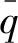
为了进一步模拟发动机内的燃烧过程，引入二阶动态环节如下

(3)

式中：Φc为发动机的控制输入；ξΦ和ωΦ均为二阶动态中的常数，且有0<ξΦ<1，ωΦ>0。则式(1)可改写如下

(4)

经过上述变换，可以得到高超声速飞行器的刚体动力学模型。显然地，该模型具有很强的非线性以及系统状态和控制输入间的耦合，难以直接用于控制器设计，因此需要对模型进行简化。根据式(4)，可以写出非线性控制系统的标准形式如下

(5)

式中：系统状态变量为x=[V,h,α,θ,Q,Φ,Ψ]T，控制输入为u=[Φc,δe,δc]T；dl为扰动；系统输出为y(t)=[V-Vref,h-href]T，其中，Vref和href分别为速度和高度的参考轨迹。

令xeq=[Veq,heq,αeq,θeq,Qeq,Φeq,Ψeq]T，定义xδ≜x-xeq，使用Jacobin矩阵线性化的方式得线性系统模型如下

(6)

式中：

1.2 高超声速飞行器的切换系统模型

由于高超声速飞行器的高度、速度、动压的变化均呈现复杂的非线性函数关系，且高超声速飞行器的飞行运动通道之间存在着强耦合特性，导致其飞行过程中的气动导数不仅与飞行器高度和速度的变化相关，还呈现出复杂的非线性变化特点[27]。这使得以动力学模型为基础的控制方法很难在高超声速飞行器进行机动时始终保持稳定。为提升系统模型精度并使动力学模型为基础的控制方法能够得到良好的应用，本节提出一种根据飞行器飞行包线分区并分别建模的高超声速飞行器切换系统模型。

图1是高超声速飞行器的飞行包线示例。可以看到，根据飞行器动压和速度将飞行包线分割成了九个区域，其具体划分方式可参见表1。根据划分方式可以得到切换律如下

σ(t)=i， (V,h)∈Ai

(7)

值得一提的是，尽管根据飞行器的速度和高度进行包线分割更为直观，但是动压的计算方式并非根据飞行速度和高度进行线性变化，因此这种分区方式会使得单一工作区内的动压存在巨大变化。飞行器动压可根据下式进行计算[28]

(8)

式中：ρ0=0.03514 kg/m3，h0=25908 m，hs=6510 m。

结合式(7)中的切换信号，可以得到高超声速飞行器面向控制的切换系统模型如下

(9)

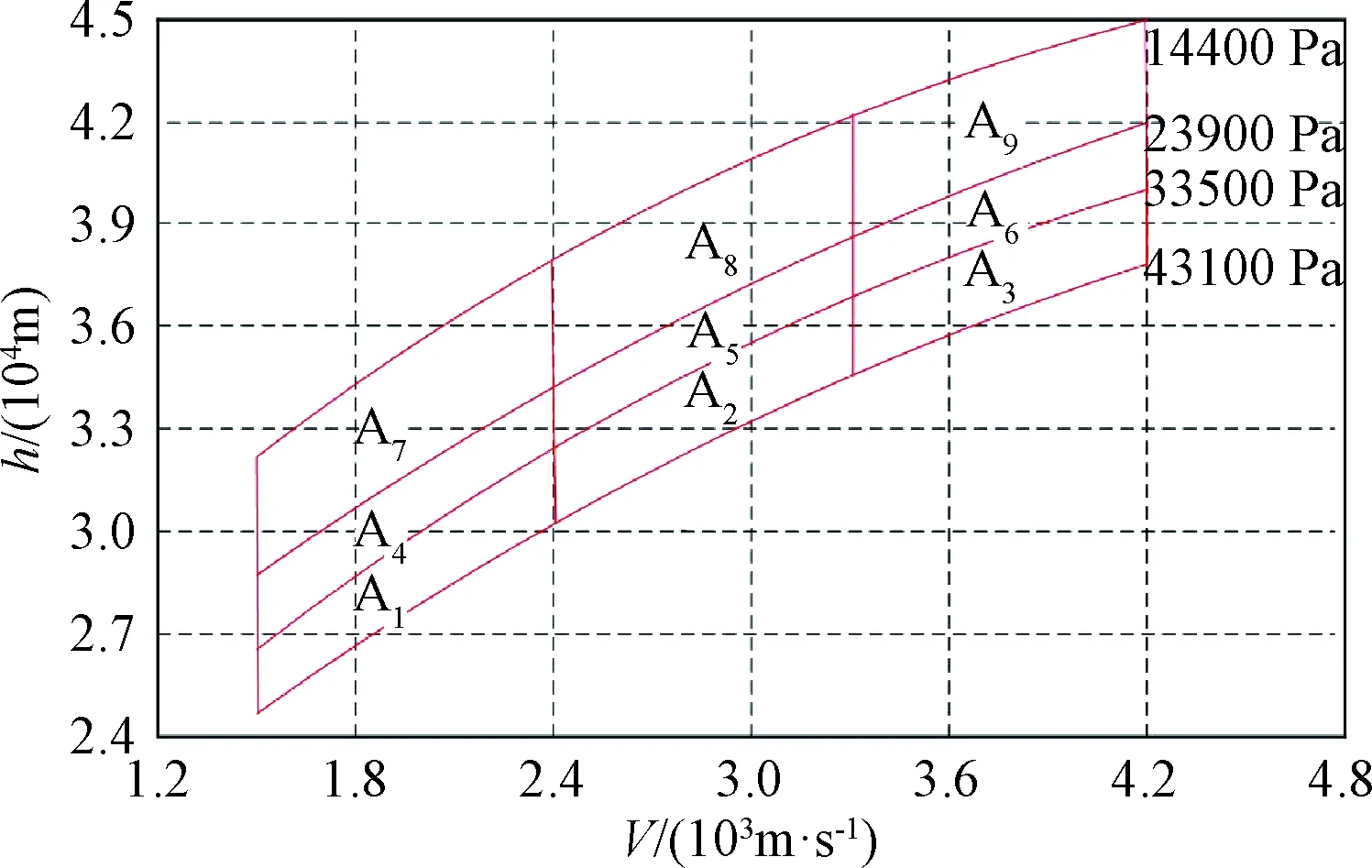
图1 飞行包线示意图Fig.1 Illustration of flight envelope

表1 飞行包线分区方式Table 1 Partition of flight envelope

本文中切换系统(9)的切换序列假定未知，但可以实时获得，其切换规律受到PDT切换信号的约束，其定义如下

定义1[29].考虑切换信号σ和切换时刻k0，k1，…，其中k0=0。若存在无限多个长度不小于τ的不相交区间，在区间内σ为常值，并且带有该性质的两个相邻区间间隔不超过TP，则称τ为持续驻留时间，称TP为持续周期。

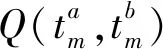
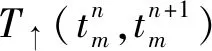
在给出高超声速飞行器抗饱和切换控制器的设计方法之前，首先给出如下引理:

(10)

(11)

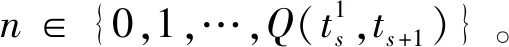
Vi(x(t))≤μVj(x(t)), ∀i≠j

(12)

若PDT信号满足

(13)

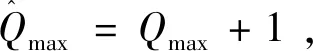
2 高超声速飞行器抗饱和切换控制器设计

高超声速飞行器在实际飞行过程中不可避免地会遇到执行器饱和的问题。因此，设计的飞行控制器需要带有一定的抗饱和机制。本节将针对高超声速飞行器建立带有执行器饱和的切换系统模型，并给出抗饱和控制器的设计方法。

2.1 带有执行器饱和的切换系统模型

考虑一类带有执行器饱和的切换系统

(14)

式中：x为系统状态；uσ(t)为控制输入；y为系统输出；σ(t)=i为切换信号。sat(ui(t))为受到执行器饱和约束的控制输入，其元素uk可由下式给出

(15)

令σ(t)=i，σ(t-τd)=j，则带有异步时滞的无约束切换控制器可由下式给出

(16)

式中：xc为控制器状态；yc,j为控制器输出(无执行器饱和时等价于系统控制输入)；Ac,j，Bc,j，Cc,j，Dc,j为具有适当维数的控制器矩阵。这里假定该控制器已经设计完毕，并且当系统不受到执行器饱和约束时，该控制器可以良好地镇定系统。

为了对执行器饱和带来的负面效果进行补偿，考虑一类具有如下形式的抗饱和补偿器

(17)

经过抗饱和补偿的控制器的形式如下

(18)

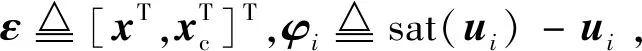
(19)

式中：

2.2 抗饱和补偿器设计

本节将针对带有执行器饱和的切换系统(14)，给出形如式(17)的抗饱和补偿器的设计方法，使得闭环系统(19)是全局一致渐近稳定的。

根据文献[31]，饱和控制输入满足如下扇形条件

(20)

式中：Wi为正定对角矩阵。根据式(17)及φi的定义可知，当ui处于饱和非线性区时，φi与φi+ui的符号相反；当ui处于非饱和线性区时，φi=0。因此扇形条件(20)必然成立。

下面给出抗饱和切换补偿器的设计方法。

定理1.考虑带有执行器饱和的切换系统(14)，令α>0，β>0，μ>1为已知常数。对于预先给定的持续周期TP，若存在正定矩阵Si，正定对角矩阵Mi，矩阵Zi，使得∀σ(t)=i，σ(t-τd)=j，i≠j，下列不等式成立

(21)

(22)

Sj-μSi≤0

(23)

式中：“*”为对应的矩阵模块的转置。

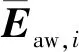
(24)

证.式(21)可分解为如下形式

(25)

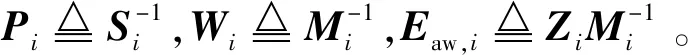
(26)

(27)

令Lyapunov函数具有如下形式

Vi(ε)=εTPiε, ∀i∈

(28)

则式(27)可改写为

(29)

同理，当式(22)成立时，可得

(30)

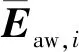
3 仿真校验

本节将通过仿真算例来对文中提出的抗饱和控制器的有效性进行校验。高超声速飞行器的初始状态如表2所示。首先根据表1中给出的分区方式，选取各区域中心点为平衡点，则可以得到形如式(11)的切换系统模型。飞行器的机动方式由下式给出高超声速飞行器系统参数的选取可参考文献[21]。其他系统相关参数给定如下：α=0.83，β=1.12，μ=1.24，采样周期Ts=0.1 s，持续周期TP=10 s，最大异步时滞τdmax=0.2 s，切换次数上限Qmax=10次。

(31)

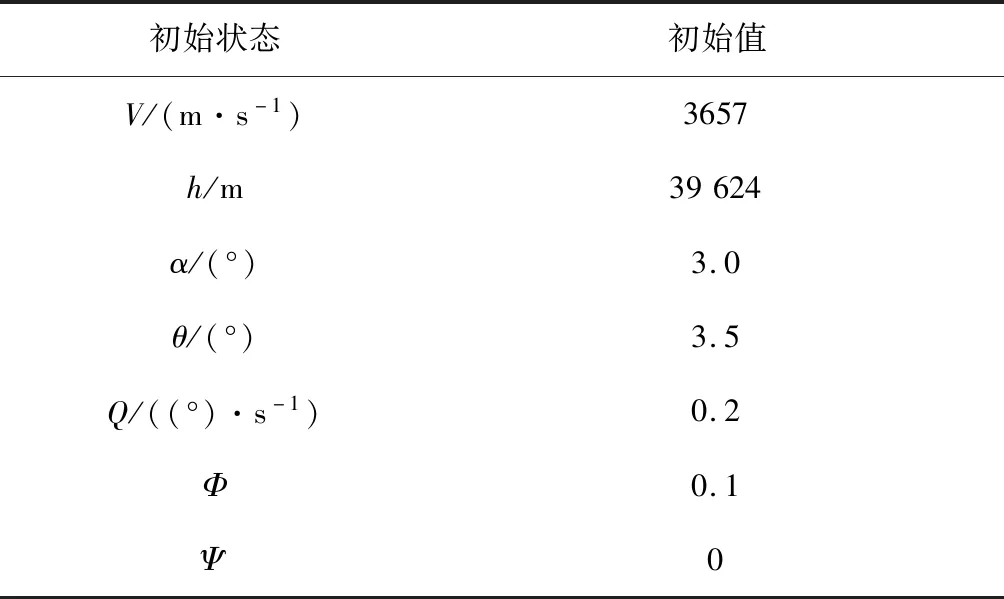
表2 高超声速飞行器初始状态Table 2 Initial state of hypersonic vehicle

为验证切换控制方法的有效性和优越性，首先对比切换控制器和一般非切换控制器的跟踪效果。采用文献[32]中的方法为各子系统分别设计控制器，并使用定理1设计抗饱和补偿器来对控制输入的饱和非线性进行补偿。通过对比使用多个子系统切换和仅使用单个子系统(本文使用A5对应的控制器)之间的跟踪效果，可以得到图2～图4中给出的仿真结果。从图2可以看出，切换控制器作用下的高超声速飞行器的运动轨迹与参考轨迹基本相符，而由非切换控制器得到的飞行轨迹则与参考轨迹之间存在着明显差距。可见切换控制器的跟踪效果要优于一般的非切换控制器。

图3和图4进一步给出了飞行速度误差和飞行高度误差的变化曲线。可以看出，切换控制器的速度误差在15 m/s左右，最大高度误差不超过150 m，而非切换控制器的速度误差可达120 m/s，最大高度误差超过760 m，两者之间的差距较为明显。造成两种跟踪控制器的跟踪误差差异明显的主要原因在于非切换控制器的系统模型中仅存在单一的平衡点，因此在高超声速飞行器跨越较大幅度的空域进行机动时，其系统模型参数的变化较大，模型失真较为明显，进而导致跟踪误差明显增大。

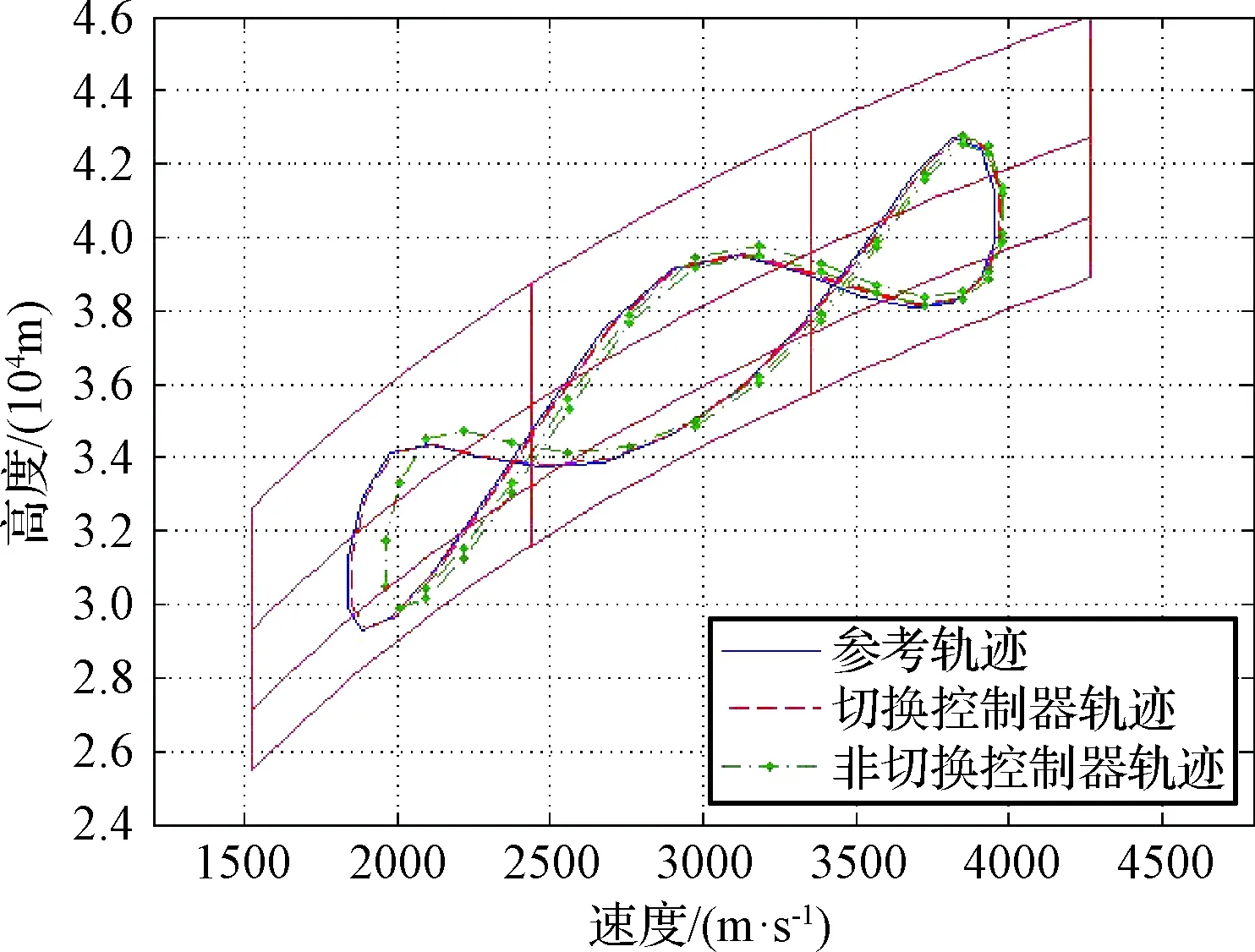
图2 飞行轨迹对比Fig.2 Comparison between flight trajectories

此外，切换控制器可将攻角的变化幅度限制在1°以内，而非切换控制器作用下的攻角变化幅度则相对较大。由于高超飞行器飞行过程中需要避免攻角过大引起的飞行器失速，可见切换控制器的效果要优于非切换控制器。由于篇幅所限，在此省略攻角的变化曲线图。

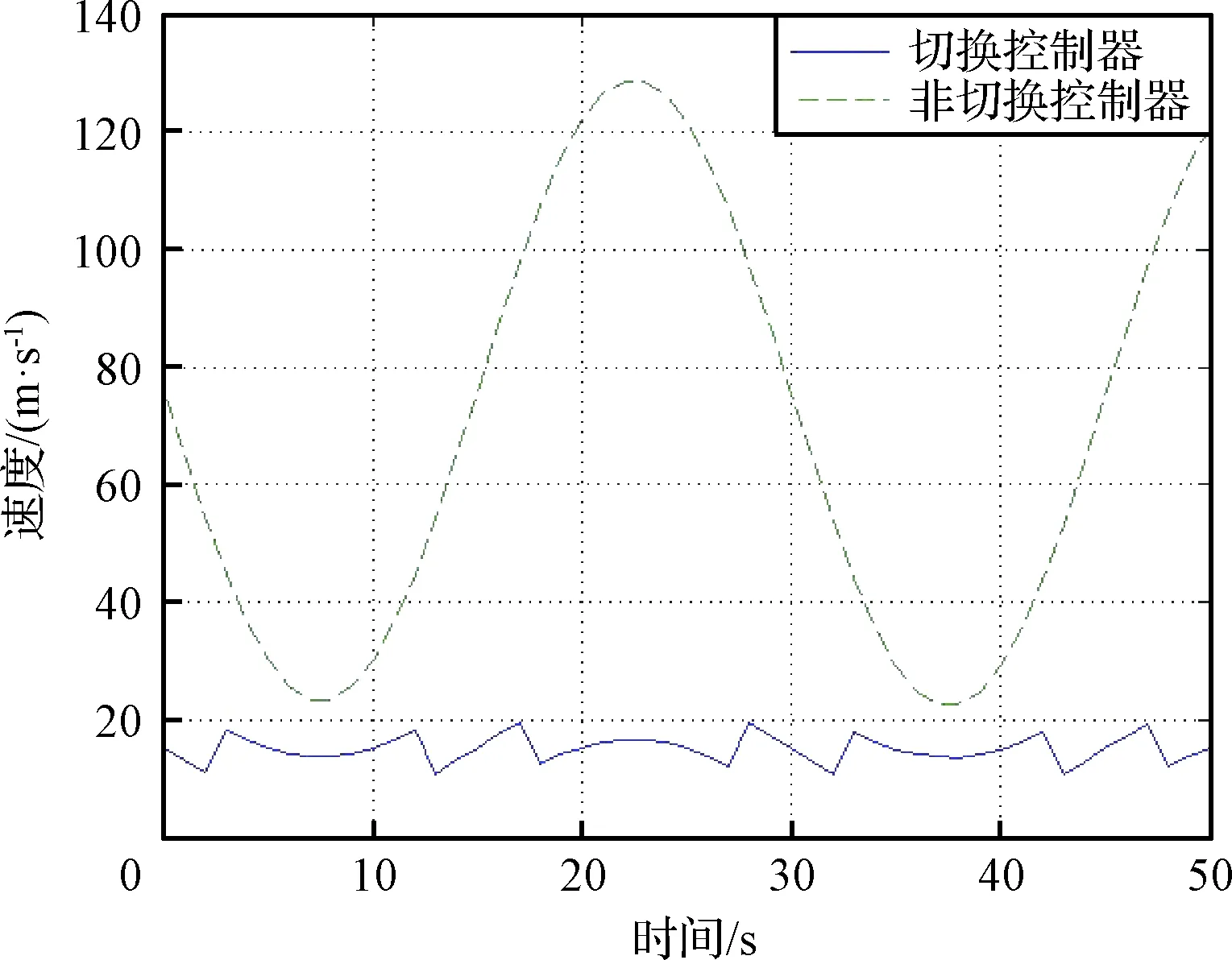
图3 飞行速度误差Fig.3 Flight velocity error

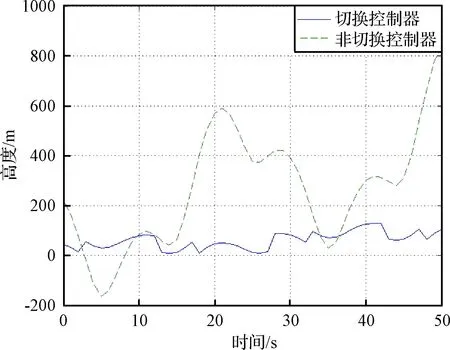
图4 飞行高度误差Fig.4 Flight altitude error

下面将对抗饱和补偿器的有效性进行进一步的验证。图5给出了是否带有抗饱和补偿器对飞行轨迹影响的对比图。可以看出，带有抗饱和补偿的控制器可以良好地跟踪参考轨迹。相对地，当失去抗饱和补偿时，飞行器无法跟踪参考轨迹且飞行轨迹超出既定的飞行包线。显然地，抗饱和补偿器是有效且必要的。

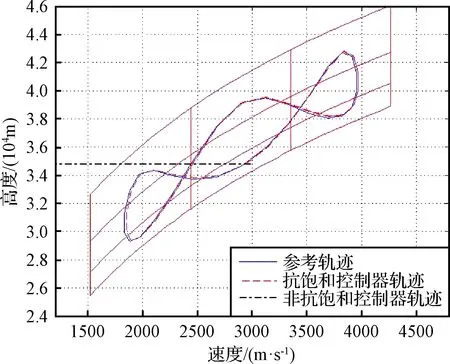
图5 是否带有抗饱和补偿器的飞行轨迹对比Fig.5 Trajectory with and without anti-windup compensator

4 结 论

本文主要研究了高超声速飞行器的抗饱和切换控制问题。首先通过对飞行包线划分区域并选取多个平衡点的方式，建立了高超声速飞行器切换系统模型。在该切换系统模型的基础上，以线性矩阵不等式的形式给出了高超声速飞行器抗饱和补偿器的设计方法，使得高超声速飞行器能够在受到执行饱和约束时进行较为复杂的机动，并能够保持系统的全局一致渐近稳定性。最后，通过仿真算例对比了切换系统模型和一般控制系统模型之间的差异，校验了切换系统模型的优越性以及抗饱和补偿器的有效性。