微型固体推进器阵列与磁力矩器联合姿态控制方法

侯晓磊，周康博，刘 勇，潘 泉

(西北工业大学自动化学院，西安 710072)

0 引 言

微型固体推进器阵列是一种近年来在皮纳卫星位姿控制中常用的新型推进器，具有体积小、重量轻、推力大、功耗低等特点[1-3]。微型固体推进器阵列的控制精度取决于单个推进器单元的推力大小，而整体推进能力取决于推进器的单元推力及阵列规模。当单个推进器推力较大时，姿态控制精度将无法保证；而推进器推力较小时，在完成大角度机动或多次机动任务中，需要的推进器规模庞大，难以达到功耗、质量以及体积等方面的限制。因此单独采用微型固体推进器阵列进行姿态控制无法满足很多实际飞行任务的需求。

为充分利用微型固体推进器的优势，需探索与其他姿态控制器联合的组合姿态控制方法。Vatankhahghadim和Damaren[4]提出的一种以脉冲动力作为辅助控制用以消除纯磁控[5-8]的增益局限和逐点不可控问题。本文以此为基础，通过设计优化点火模型并设置微型固体推进器阵列补偿控制时间，对联合控制算法进行改进，针对大角速度阻尼问题和大角度姿态捕获问题，提出了以磁力矩器作为主执行器，以微型固体推进器阵列作为辅助控制执行器的皮纳卫星姿态联合控制算法[9-11]。本文所提算法充分利用微型固体推进器阵列大推力的特点，将微型固体推进器阵列作为高机动状态下的速度控制以及磁控能力较弱时的姿态辅助控制，在保证卫星姿态控制精度的前提下，提高了姿态控制的响应速度，扩大了控制器在不同空间环境条件下的适用性。

1 优化点火模型

为输出参考控制力矩而对指定位置的推进单元进行点火的组合点火算法是基于固体脉冲式推进器阵列的皮纳卫星的姿态控制系统的核心问题。本文采用0-1规划[12]建立微型固体推进器阵列优化点火模型，并解决推进器阵列的组合选择问题。

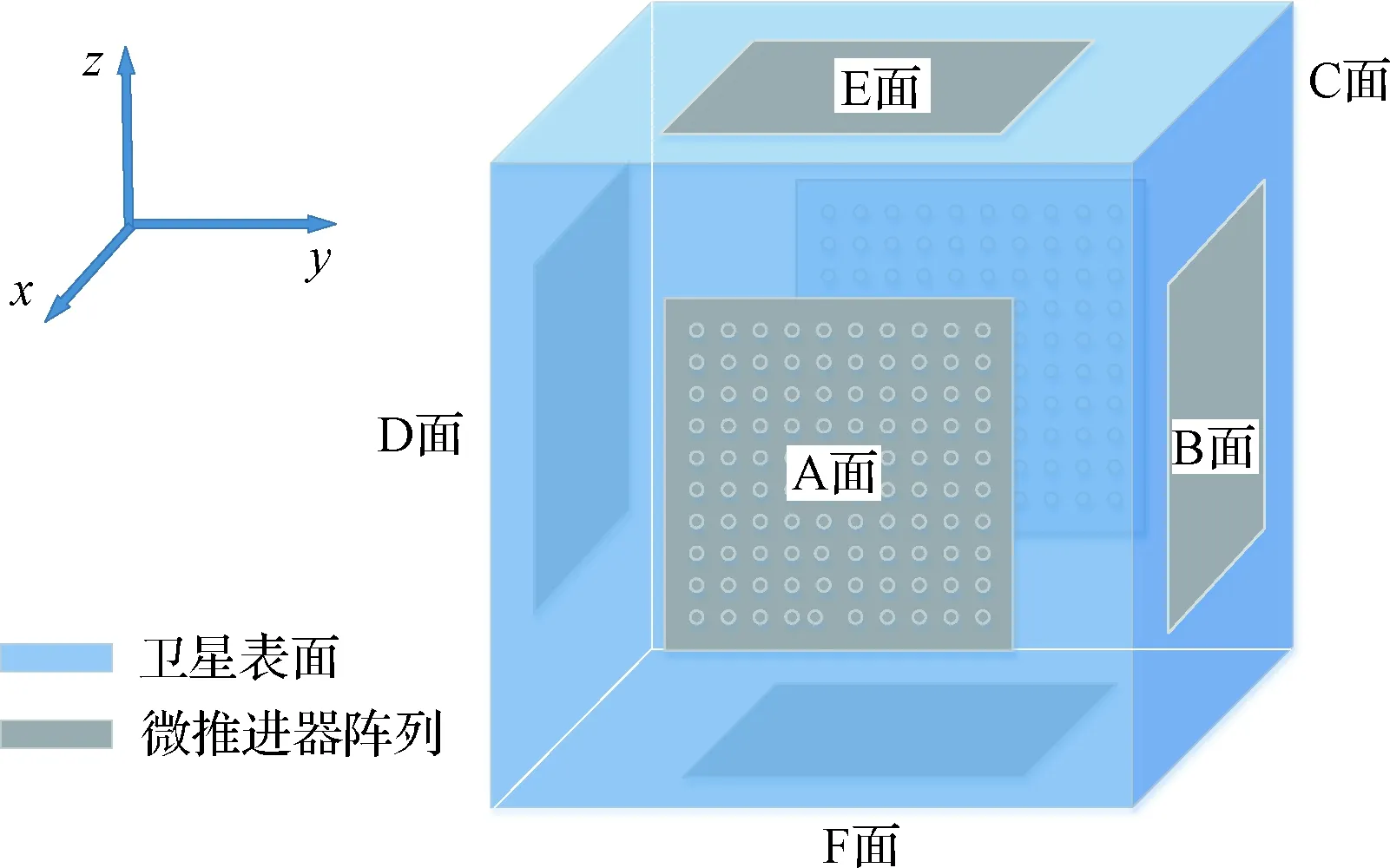
图1 卫星表面阵列配置示意图Fig.1 Distribution of MEMS solid propellant thruster array on satellite surface

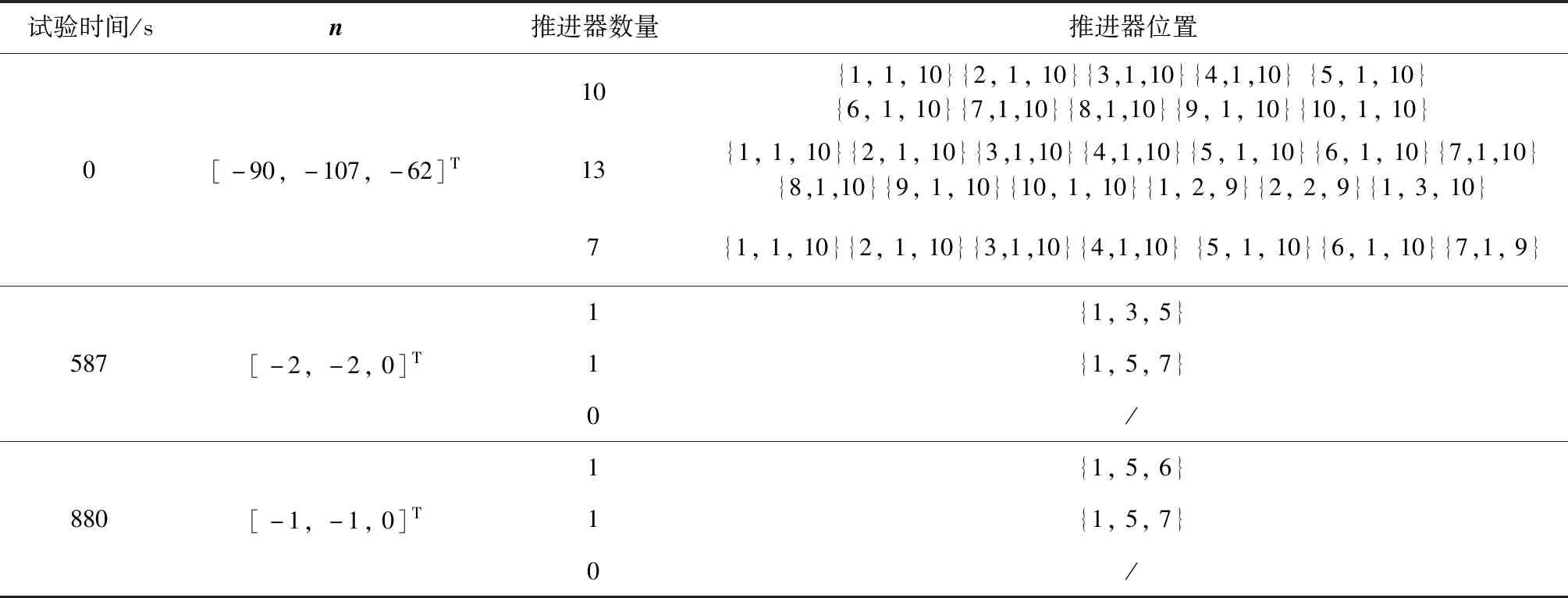
本文采用解耦方法，按照相对的两个阵列为一组的方式将6个推力器阵列分为3组，按照力偶的形式提供控制冲量矩，且要求每组力偶仅在一轴的方向上产生作用，每个面上微型固体微推进器阵列形心与所在卫星表面形心相重合。表1给出了三组控制量的分配方式。

以Z轴控制为例介绍点火方案。图2为10×10的A面微型固体推进器阵列，相邻两个推进器之间的距离均为lmin，分别沿Y轴正方向和Z轴负方向将点火点编号，每个推进器为单粒装药。根据表1结果，A面阵列控制星体系Z轴方向，以中轴线为界将阵列分为两部分，图2中6～10列控制Z轴正方向，1～5列控制Z轴负方向。为了避免产生通过星体质心的推力，应使C面点火点与A面的点火点同排，使得产生的力偶方向与Z轴方向重合。

表1 控制量分配表Table 1 Control allocation

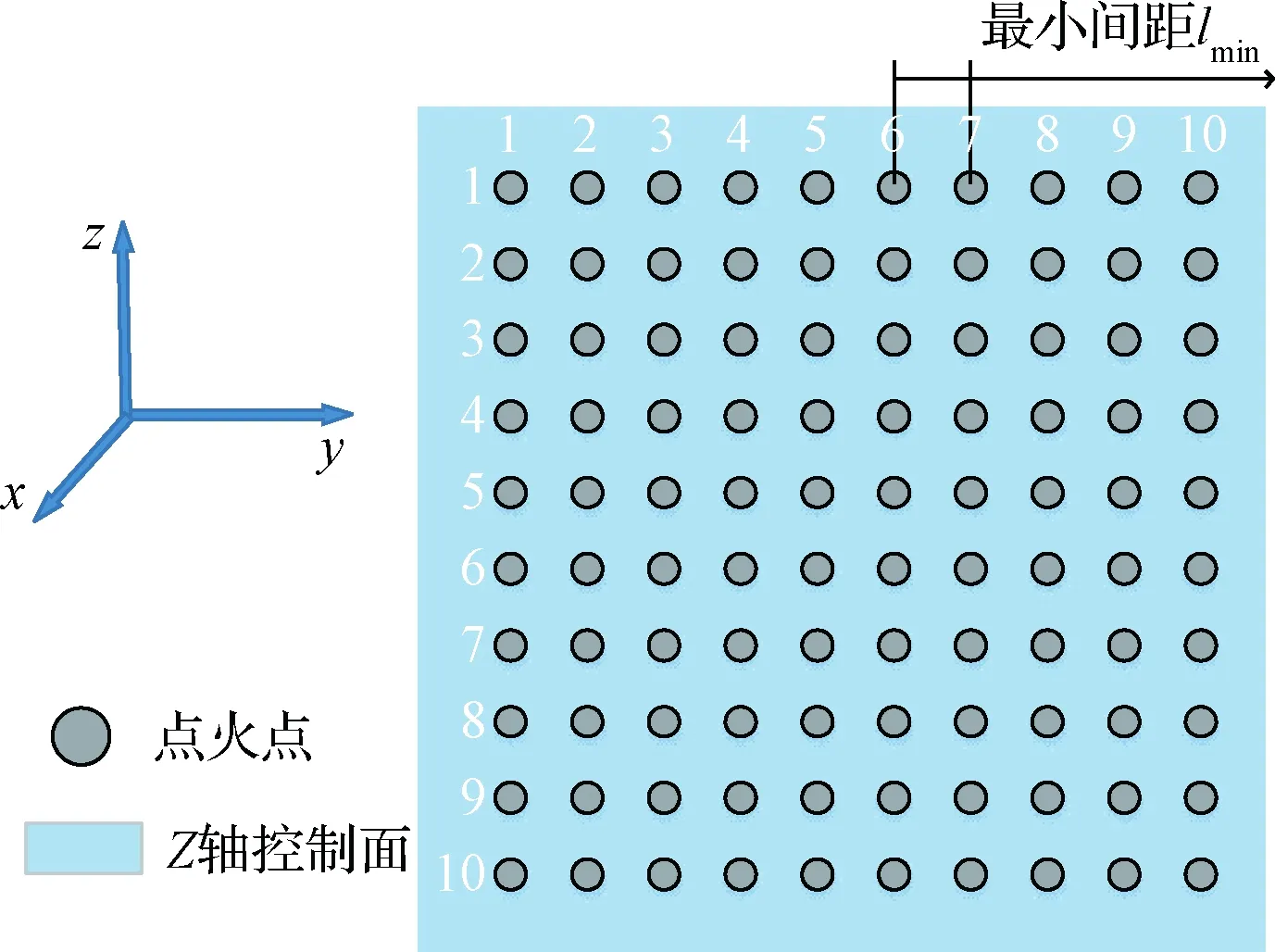
图2 A面阵列控制方向示意图Fig.2 Attitude control via A-side

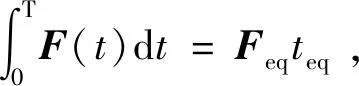
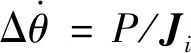
在此前提下，提出了微型固体推进器阵列优化点火模型设计：

1) 使用的推进器组合数量最少。

2) 同行不同列的推进器的优先级相同。

3) 同列不同行的推进器的优先级取决于该行剩余推进器数量。剩余数量越多，优先级越高。

下文以X轴为例介绍微型固体推进器阵列优化点火算法。

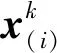
(1)

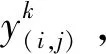
(2)

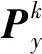
(3)

根据上述定义，第k次点火后的状态矩阵表示为：

(4)

定义Sk为第k次点火时的目标函数，满足上述约束条件，则微型固体推进器阵列优化点火模型目标函数为：

(5)

式中:|x|表示向量x中元素的个数。

综上，微型固体推进器阵列的优化点火问题可以描述为：

i∈[1,N]，j∈[1,N]

(6)

上述问题是典型的0/1规划问题，由于计算机性能限制，为简化计算，本文采用贪心算法[15]进行模型求解，即可得到具体的推进器组合。

2 微型固体推进器阵列补偿控制时间设置

由于磁力矩器输出力矩在轨道中不同位置的差异导致采用纯磁力矩器的皮纳卫星姿态控制系统在特定轨道时间内存在控制能力缺陷，导致姿态控制响应慢、指向精度差等问题。在磁力矩器控制能力较差的轨道时间内，采用微型固体推进器阵列进行补偿控制，可以有效的提高皮纳卫星在此时段内的控制能力，从而保证姿态控制响应速度以及指向精度。

本文通过计算小时间窗的宽度Δt跨越总旅行时间的可控性来评估皮纳卫星姿态控制系统中磁力矩器的控制性能。

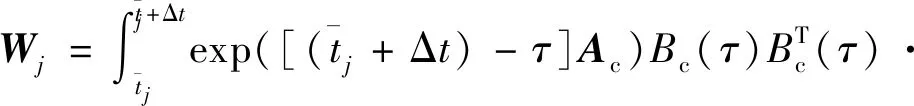
(7)

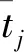
Wj若是非奇异的，则系统是可控的。Wj的值主要根据轨道倾角以及轨道高度的不同产生变化。通过确定该矩阵的最小特征值到达每轨的局部最小值来选择微型固体推进器阵列进行补偿控制的时间。

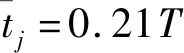
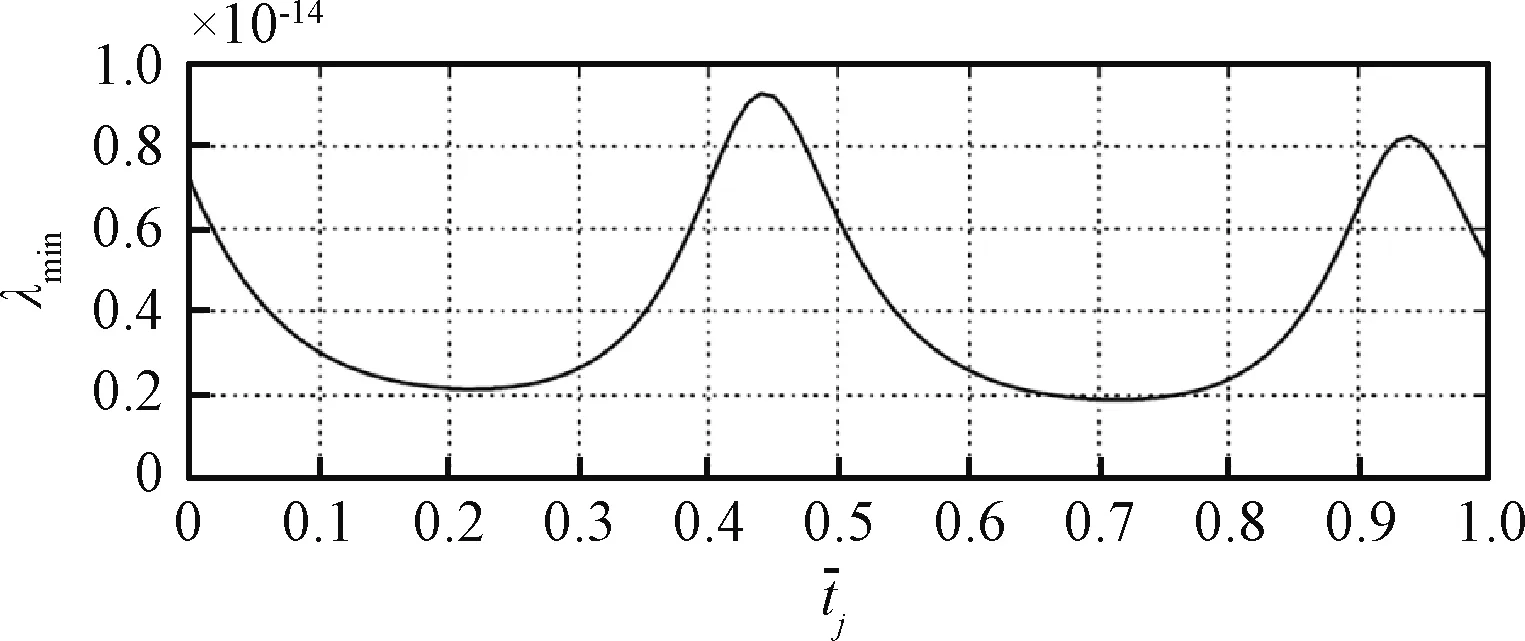
图3 Gramian矩阵的最小特征值[4]Fig.3 The minimum eigenvalue of Gramian matrix

3 速度阻尼联合控制律设计

3.1 控制律设计流程图

根据微型固体推进器阵列以及磁力矩器各自的力矩输出特点，在皮纳卫星联合速度阻尼控制过程中，首先利用微型固体推进器阵列的大机动能力，使卫星角速度状态迅速变化到既定阈值以内，再根据B-dot控制律[16]利用磁力矩器进行微调，此外，在磁力矩器控制能力较弱的区域，利用微型固体推进器进行补偿控制，从而大幅度提高控制响应速度、缩短控制周期。微型固体推进器阵列与磁力矩器联合速度阻尼控制流程如图4所示。

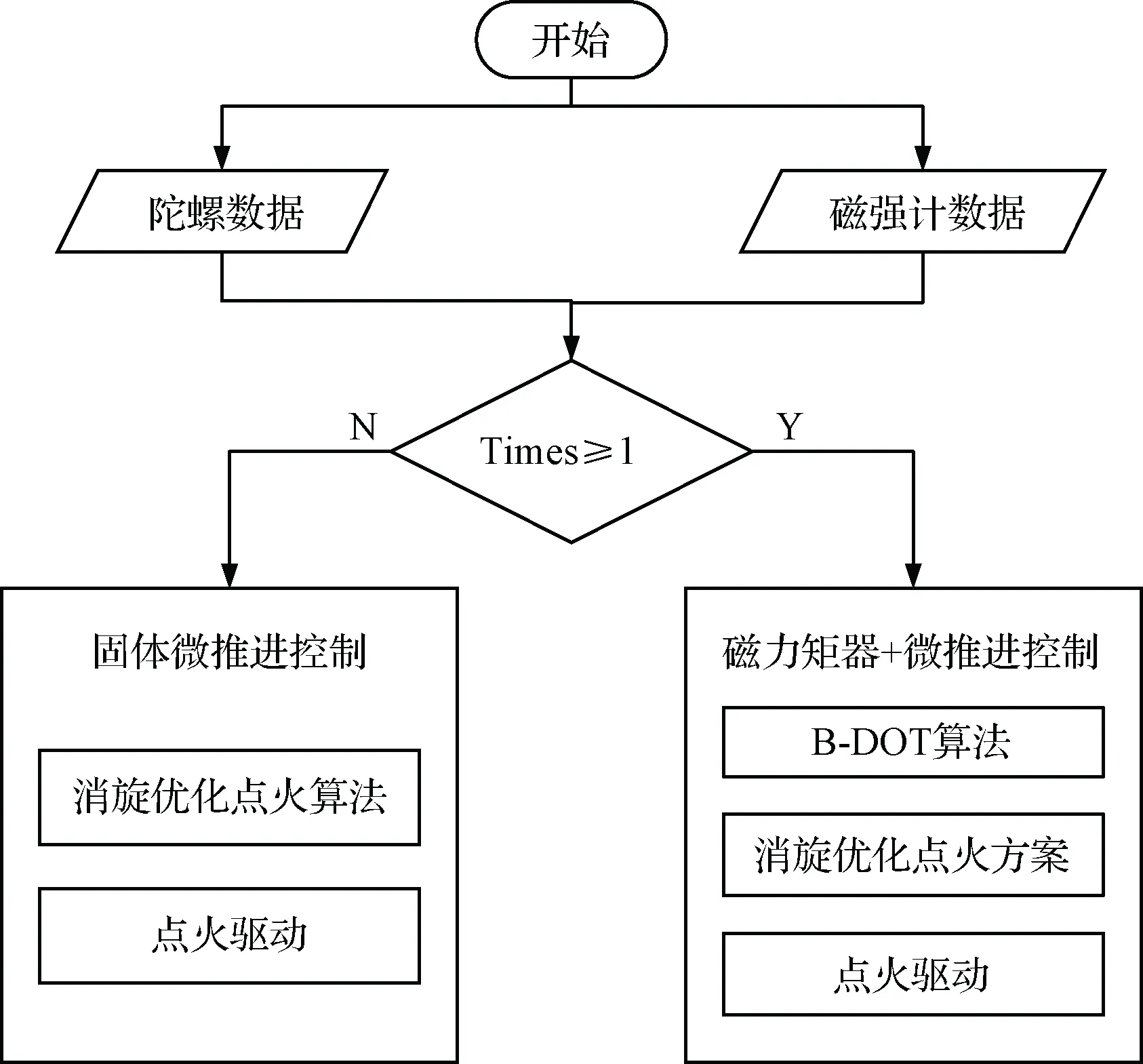
图4 微型固体推进器阵列与磁力矩器联合速度阻尼控制流程图Fig.4 Flow chart of joint velocity damping control for MEMS solid propellant thruster array and magnetic torquer

3.2 微型固体推进器阵列大角速度阻尼控制律

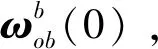
3.3 微型固体推进器阵列辅助速度阻尼控制律

作用在卫星上的总力矩由磁力矩器输出力矩和微型固体推进器阵列的输出力矩共同输出，假设微型固体推进器阵列作用时间为tk，k∈{1,2,…,M}。忽略其他干扰力矩，卫星的动力学方程为：

(8)

用δ(t-tk)描述微型固体推进器阵列用以描述脉冲输出的特性，因此选取卫星相对于惯性系的旋转能量作为Lyapunov函数V(x)，可以表示为：

(9)

(10)

忽略其他干扰力矩，作用于星体上的力矩全部由磁力矩器和推进器产生，则式可以整理为：

(11)

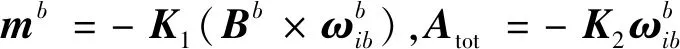
(12)

式中:S(ε)为斜对称矩阵，表示为:

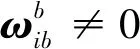
(13)

综上，则连续/脉冲混合系统速度阻尼控制律为：

(14)

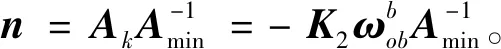
4 基于混合系统模型的姿态捕获联合控制律设计

4.1 控制律设计流程图

在皮纳卫星进行姿态捕获过程中，由于微推进器阵列无法避免空间环境力矩干扰，且控制精度有限，因此仍采用磁力矩器作为主要执行器，而微型固体推进器阵列作为辅助执行器；在磁力矩器控制能力较弱时，则采用连续/脉冲结合的联合控制方案增强控制性能，从而缩短姿态捕获周期，提高控制精度。微型固体推进器阵列与磁力矩器联合姿态捕获控制流程如图5所示。

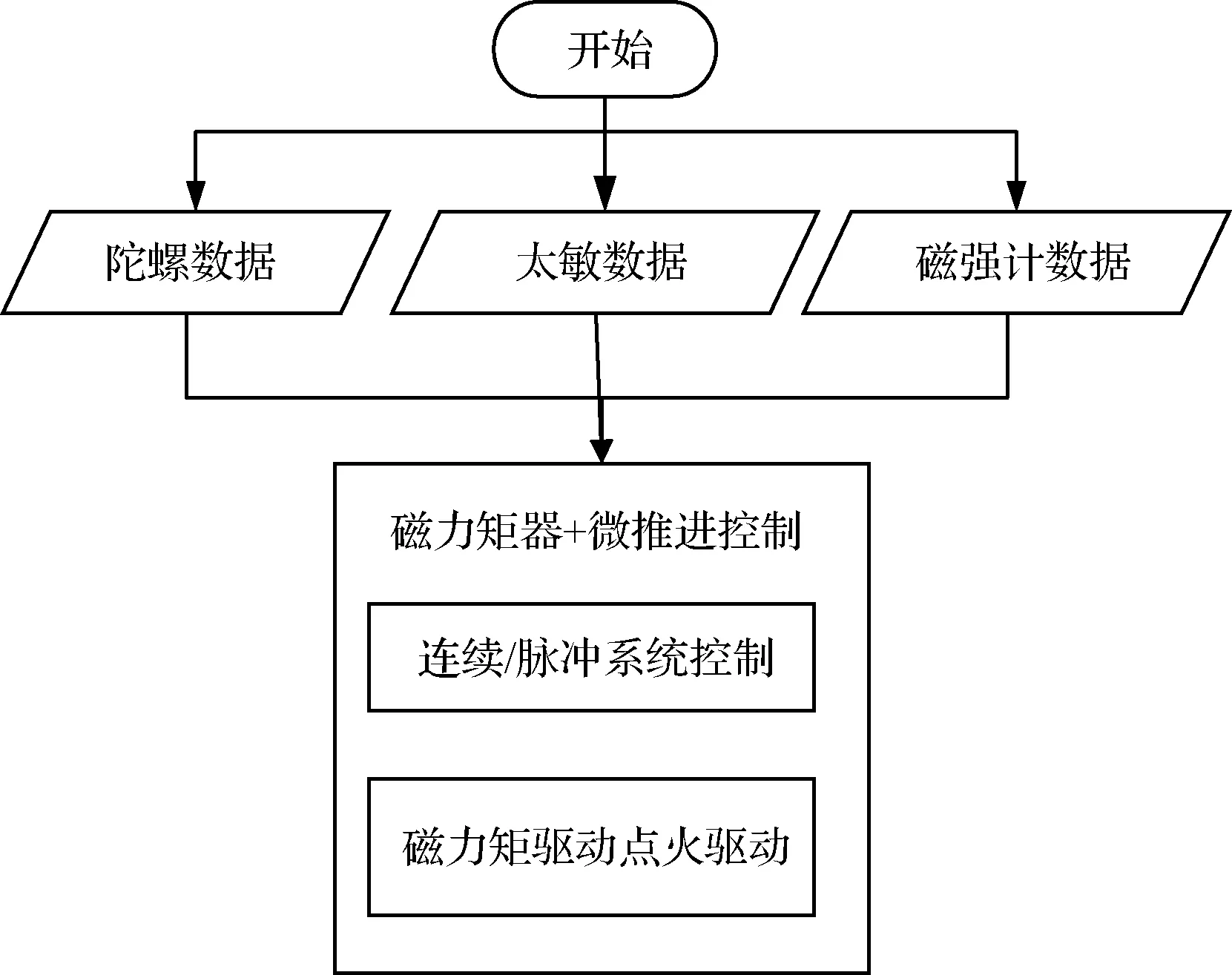
图5 微型固体推进器阵列与磁力矩器联合姿态捕获控制流程图Fig.5 Flow chart of joint attitude acquisition control for MEMS solid propellant thruster array and magnetic torquer

4.2 姿态捕获联合控制律设计

1)连续/脉冲的混合系统模型

对于一个连续/脉冲的混合系统，脉冲施加在tk，tk∈N时刻，可以表示为y=ζhu，其中，u={uc(t),udk}同时包含连续和离散的控制输入，同理，y={yc(t),ydk}同时包含连续和离散系统的输出。假设uc和yc,udk和ydk分别具有相同的维数。

设初始状态量x(t0)=x0，可以得到在t≠tk的连续函数表达式为

(15)

同理，得到在t=tk的离散函数表达式为：

(16)

式中:x(t):R+→Rn×1为状态矢量，uc(t):R+→Rmc×1和udk:N+→Rmd×1为控制输入，yc(t):R+→Rmc×1和ydk:R+→Rmd×1为控制输出。且连续状态空间函数Ac，Bc，Cc和Dc以及离散状态空间函数Adk，Bdk，Cdk和Ddk维数相同。

根据姿态运动学和动力学方程，得到如下所示的混合系统的线性模型

(17)

2)控制律设计与证明

系统输入表示为：

(18)

令P=[P1,P2]，将系统输入带入混合系统线性模型，得到：

(19)

(20)

(21)

为了方便讨论，令

k∈{1,2,…,M}，t∈[tk-1,tk)

(22)

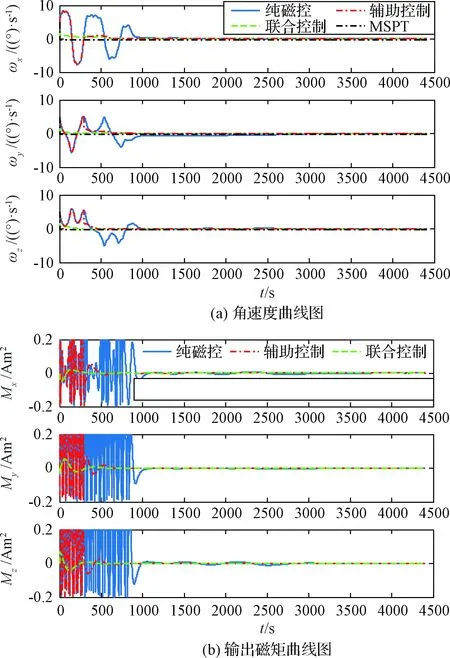
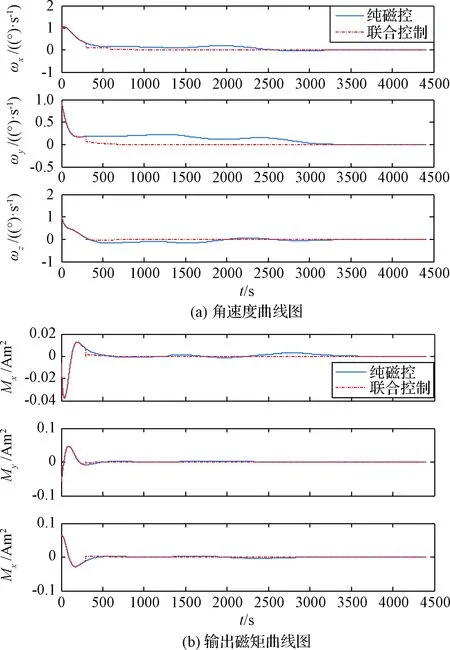
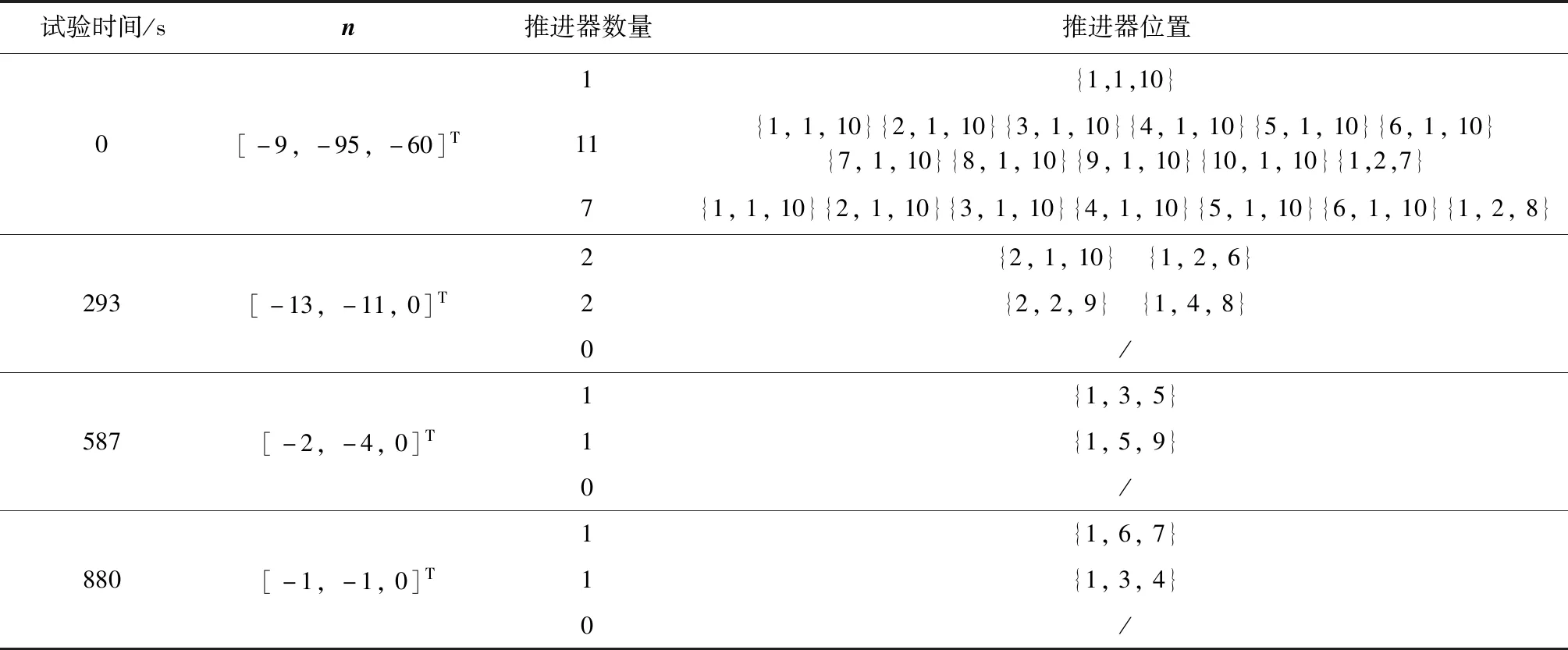
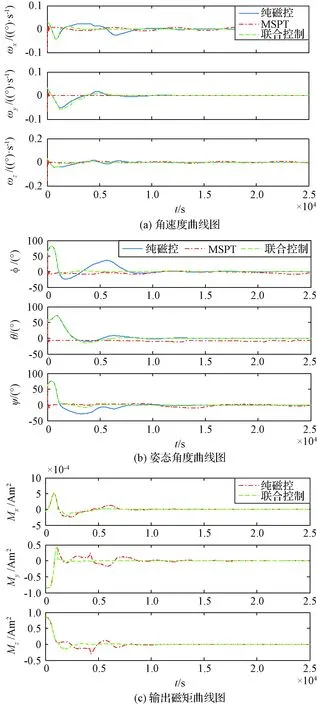
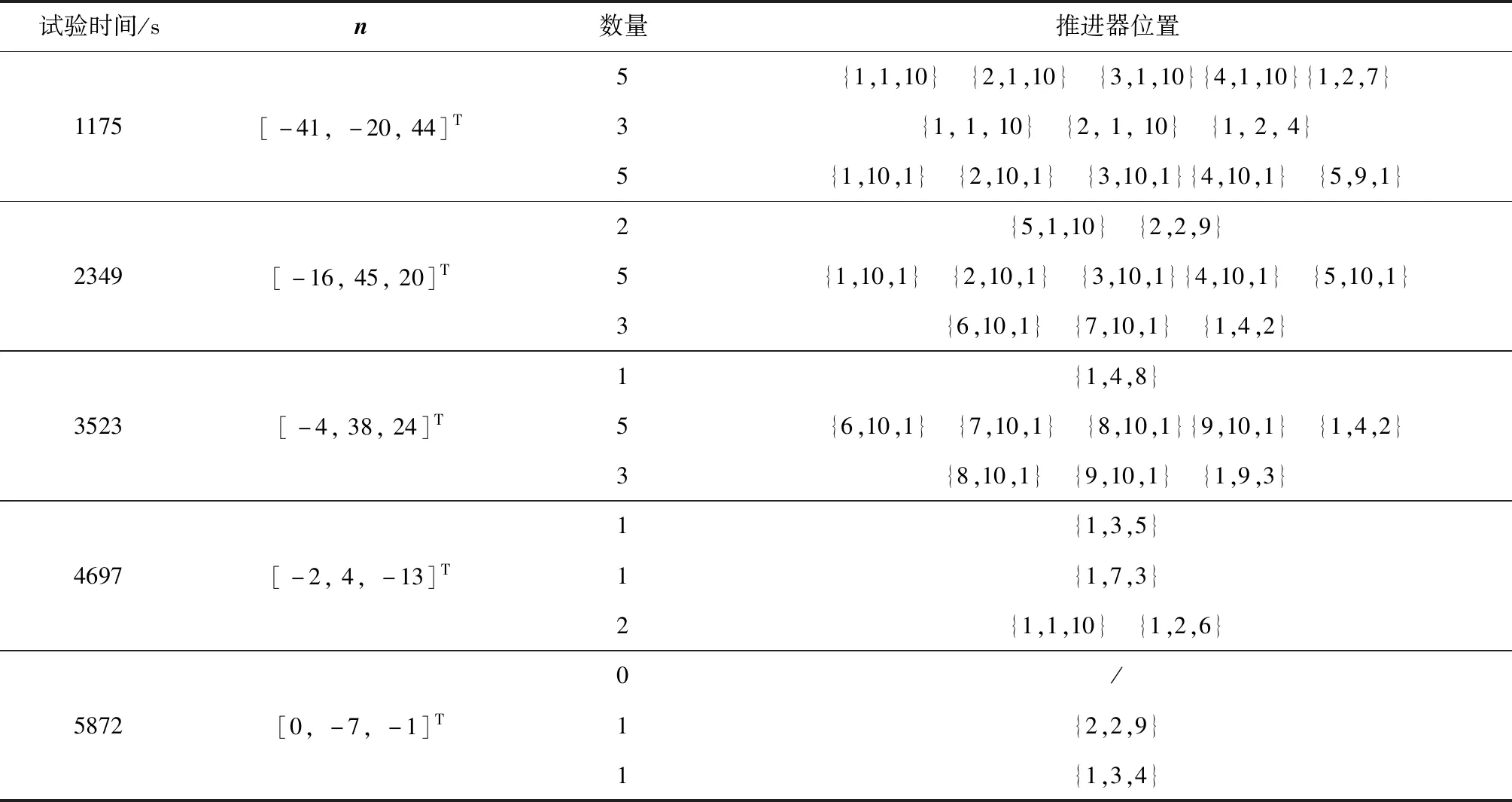
若矩阵Ψk对所有k

5 仿真校验

不考虑其他干扰力矩的影响，卫星轨道高度为682 km，轨道倾角为97°，惯性矩阵J=diag(1.5×10-1,1.8×10-1,1.1×10-1) kg·m2，初始姿态角为[60°, 60°, 60°]，磁力矩器最大输出磁矩0.2 Am2，固体微推进器单位推力为42.6 N·m。

5.1 速度阻尼联合控制律校验

根据初始角速度大小，设计两组仿真对比实验。磁控增益系数矩阵K1=diag(1.2×105,1.2×105,1.2×105)，控制律为K2=diag(0.91×10-2,1.08×10-2,0.62×10-2)。大角速度阻尼实验的初始角速度为[5 °/s, 5 °/s, 5 °/s]，小角速度阻尼实验的初始角速度为[1 °/s, 1 °/s, 1 °/s]。

大角速度阻尼实验结果如图6 (a)、(b)所示，微型固体推进器阵列与磁力矩器联合速度阻尼方法的稳定周期为1602 s，1752 s和1643 s，后控制精度可以达到5×10-3°/s, 0.017°/s和0.013°/s。由仿真结果可以看出，联合控制方法所需的角速度收敛时间与输出磁矩明显低于其他传统算法；辅助控制方法的角速度收敛速度和所需的输出磁矩在290 s之后三轴角速度的收敛速度都明显快于纯磁控方法，所需磁矩也明显降低。从表2中结果可以看出，微型固体推进器阵列共进行了3次点火，三轴消耗的推进器数量分别为12，15和7。

纯磁控方法三轴稳定周期为3045 s，3815 s和3351 s，三轴稳定精度为0.015 °/s，0.013 °/s和8×10-3°/s。对比表明，联合控制方法相较于传统磁控方法在相同的控制精度的前提下，控制角速度周期缩短了48%，54%和51%，且大幅度降低了振荡幅度；同时降低了系统的能量输出。

表2 大角速度联合阻尼控制微型固体推进器阵列点火位置表Table 2 Ignition position of MEMS solid propellant thruster array under large angular velocity using joint velocity damping control

纯微型固体推进器阵列控制虽能快速降低卫星旋转，但是控制精度受限于本身推进器的性能以及敏感器误差。仿真结果显示其三轴控制精度仅有0.3325°/s，0.2823°/s和0.3143°/s，无法满足实际任务需求和姿态捕获任务的初始精度要求，且可靠性无法得以保证。

图6 大角速度阻尼Fig.6 Large angular velocity damping

图7 小角速度阻尼Fig.7 Small angular velocity damping

本文同时对只采用微型固体推进器阵列辅助控制的方案进行验证，其控制精度与纯磁控方法以及联合控制方法相近，约为0.011°/s,0.012°/s和0.015°/s。控制时长处于两者之间，约为2103 s，2245 s和1986 s。表3中结果表明，微型固体推进器阵列共进行了4次点火，三轴消耗的推进器数量分别为5，15和7对，略小于联合控制所需要的微推进器数量。

小角速度阻尼实验结果如图7 (a)、(b)所示，纯磁控方法角速度控制周期平均约为3102 s，而联合控制方法周期平均仅有722 s，相比纯磁控方法提高了76.72%。表4结果表明，联合控制方法仅需两次脉冲，三轴共消耗4对微推进器阵列。因此在初始角速度较小时，在保证控制精度相同的前提下，联合控制律仅需消耗较少的微推进器组合，能有效缩短控制周期，降低振荡幅度。

表3 大角速度辅助阻尼控制微型固体推进器阵列点火位置表Table 3 Ignition position of MEMS solid propellant thruster array under large angular velocity using auxiliary velocity damping control

综上所述，微型固体推进器阵列与磁力矩器联合速度阻尼控制方法在保证角速度的精度的前提下，能够有效缩短控制周期，同时降低系统的振荡幅度。

表4 小角度微型固体推进器阵列点火位置表Table 4 Ignition position of MEMS solid propellant thruster array under small angel

5.2 姿态捕获联合控制律校验

将本文提出的联合控制方法与传统的纯磁控方法以及纯微型固体推进器阵列控制方法进行比较。旋转角速度为[0.05°/s, 0.05°/s, 0.05°/s]。纯磁控方法角速度增益系数矩阵为K1=diag(3.11×102,3.11×102,3.11×102)，欧拉角增益系数矩阵为K2=K2/1000；微型固体推进器阵列控制角速度增益矩阵为Kmspt1=diag(2×10-2,2×10-2,2×10-2)。欧拉角增益系数矩阵为Kmspt2=Kmspt1/1000。仿真结果如图8所示。

图8(a)是四种控制算法的角速度曲线图，其中微型固体推进器阵列与磁力矩器联合姿态控制方法的姿态稳定周期为5466 s，6165 s和6435 s。20 000 s后，欧拉角控制精度可以达到0.3°,0.2°和0.4°，角速度控制精度可达0.8×10-3°/s，1.1×10-3°/s和2×10-3°/s。与纯磁控方法相比，联合控制方法中三轴所需的输出磁矩明显降低。从表5中结果可以看出，微型固体推进器阵列共进行了5次点火，三轴消耗的推进器数量分别为9，15和14对。

图8 姿态捕获控制Fig.8 Attitude acquisition control

相比而言，纯磁控方法达到上述姿态稳定精度时需要16 874 s，17 923 s和18 567 s，因此微型固体推进器阵列与磁力矩器联合捕获控制的效率相比于该算法三轴分别提高约208%，191%和188%，从而大大缩短捕获周期。20 000 s后，联合控制方法平均角速度控制精度为1.3×10-3°/s，相比纯磁控方法的5×10-3°/s提高了约2.3倍。对比表明，联合控制方法相较与传统磁控方法在相同的控制精度的前提下，能有效缩短姿态控制周期，降低振荡幅度，节省系统输出能量。

纯微型固体推进器阵列控制所需要的推进器数量为70，35和100对，远多于联合控制方法所用推进器数量，其欧拉角和角速度的稳定精度分别为8°和1.3°/s。另外，Z轴角速度曲线一直处于持续振荡，直至所有推进器耗光，可靠性无法得以保证，因此无法满足对地指向和对地通信等实际任务需求。

综上所述，微型固体推进器阵列与磁力矩器联合姿态捕获控制方法在保证角速度与欧拉角精度的前提下，能够有效缩短控制周期，同时降低系统的振荡幅度，从而验证该算法的有效性。

表5 姿态捕获控制微型固体推进器阵列点火位置表Table 5 Ignition position of MEMS solid propellant thruster array using attitude acquisition control

6 结 论

本文针对皮纳卫星姿态控制系统中采用纯磁控方法与纯微型固体推进器阵列控制方法中存在的问题，提出了同时采用两种执行机构的皮纳卫星姿态联合控制算法，并利用Lyapunov稳定性理论证明了算法的稳定性。仿真结果表明，相较于传统的纯磁控方法，所提姿态联合控制算法能够有效提高控制精度，大幅度缩短控制周期。由于微型固体推进器阵列和磁力矩器均具有质量轻，功耗低，且价格低廉等优点，因而这种联合控制方法在低成本高精度的皮纳卫星姿态控制系统具有良好的发展前景。