对几个数学问题的思考
2020-04-13张承宇
张承宇
(深圳市中小学学科竞赛学会 518001)
有几个常见的数学问题流传很广,长期以来,有些老师以及某些数学参考资料对这些问题的分析与解答有的有误,有的分析片面,对学生造成很不好的影响.笔者认为,现在有必要对这几个问题予以澄清,以正视听.下面谈谈笔者对这几个问题的思考.
1.不久前,笔者看到一道有趣的“字谜”测试题:
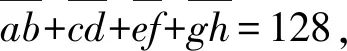
(a+c+e+g)×(b+d+f+h)
的值是.
答案是280.
原标准解答是:如果有一个十位数字大于4,至少是5,则十位数字之和不小于1+2+3+5=11,因此个位数字之和将不超过18. 此时4个个位数最小和为4+6+7+8=25 ,矛盾!因此十位数字不能大于4,故4个不同的十位数字只能是1,2,3,4. 进而可知个位数字只能是5,6,8,9. 故
(a+c+e+g)(b+d+f+h)=(1+2+3+4)×(5+6+8+9)=10×28=280.
笔者认为,上述解答不够完整,它只说明了必要条件,对这种解答,我们提出二个问题:一. 是否存在四个二位数,其和为128? 二. 符合条件的四个数,是唯一存在的吗?
对学生进行问题讲解时 ,必须讲清楚上述两个问题.
如果能举出一个例子,这两个问题都解决了.如:19+28+36+45=128.
这里举出实例“19+28+36+45=128”很重要,因为,前面所述的推理只能说明答案有可能是280,但是,不代表一定存在结果等于128的算式.当然,作为填空题,我们看不到考生的解答过程.
2.小卖部规定4个汽水瓶可以换1瓶汽水,鹏程幼儿园大班小张阿姨买了21瓶汽水,喝完后再用空瓶去换……结果班上每位小朋友刚好每人一瓶,那么该班有______名小朋友.
笔者看到的解答是:先将21瓶汽水喝完,用其中20个空瓶换5瓶汽水,喝完;现在有6个空瓶,再用其中4个空瓶又可以换1瓶汽水,喝完;此时还有3个空瓶,然后借1瓶汽水喝完,将四个空瓶抵1瓶汽水还给店主.故班上共有21+5+1+1=28(人).
当下流行的这种解答,甚至上了电视娱乐节目,当主持人说道“先借一瓶汽水,喝完后还店主4个空瓶”,场下掌声雷动.殊不知,这不应该是一个真正的数学老师的解法.
下面笔者给出一种更为合理,更有数学味的解答:
解: 4个空瓶换1瓶汽水,等价于3个空瓶可以喝1瓶汽水(不要店主的瓶),那么,21个空瓶可以喝到7瓶汽水, 21+7=28,因此,班上共有28人.
3.笔者本人1996年原创的一道题目,发表在《数学通报》1996年第10期“数学问题解答”栏目,答案发表在第11期上. 即以下
题1038在正方形纸片上有1996个点,加上正方形的顶点共2000个点,且这些点中任意三点都不在一条直线上,现在以这2000个点为顶点,将正方形纸片剪开,问最多能剪成多少个三角形纸片?
题目慢慢传开后,就出现了一种错误的解法(以下解法一),大多数老师和学生都是这样做的:
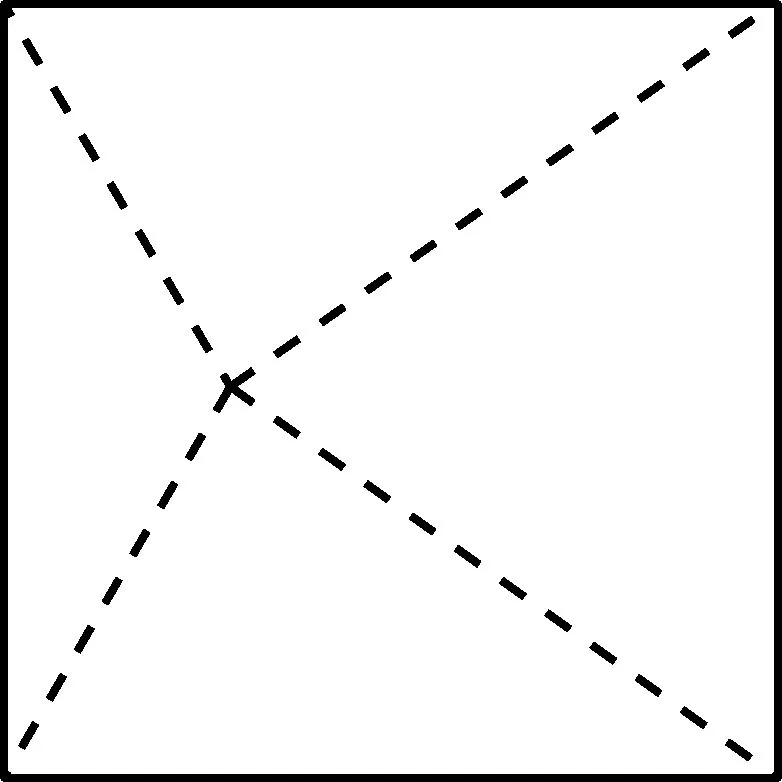
解法一:如图,纸上有一个点,最多可剪4个小三角形,如果增加一个,则这个点必在某个三角形内部,不会在边上,因为没有三点共线,这样,就把该三角形一分为三,增加了2个三角形,……,如此推知,最多可以剪出
4+2×(1996-1)=3994
个三角形.
为什么这个解答是错的(尽管最后答案是正确的)?因为这种剪法只是千千万万种剪法中的一种,你怎么能证明别的剪法不会剪出更多的小三角形?若纸片上有两个点,就会出现以下不同的剪法:
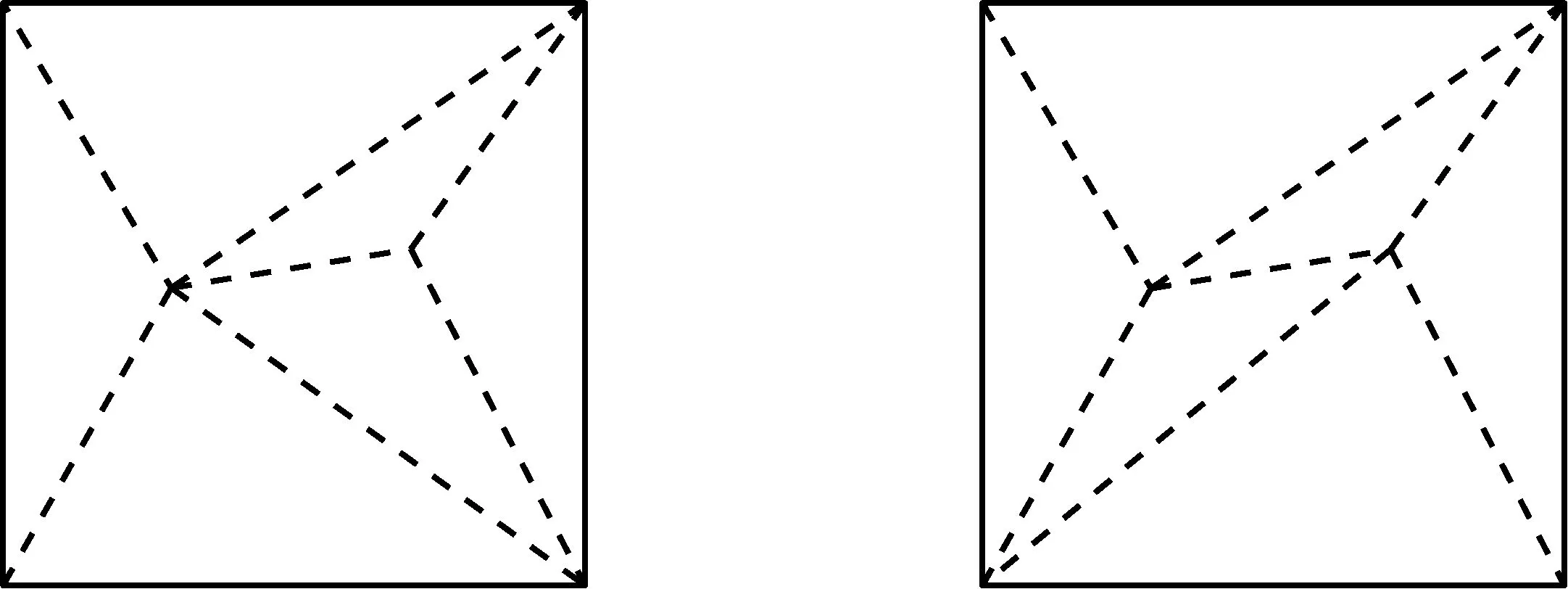
正确的解法应该是:
解法二: (刊于《数学通报》1996年第11期“数学问题解答”栏目)

易知,在剪成的三角形纸片上不应该再有点,否则三角形个数不是最多.现在计算所有这些三角形内角和.为此将它们重新拼成正方形,发现这些角分为两类:一是以正方形的4个顶点为顶点的,再是以1996个内点为顶点的,对于前者,这些角拼成了4个直角,对于后者,这些角拼成1996个周角.所以总和为90°×4+360°×1996.因此三角形个数为
解法三: 设正方形纸片上有n个点时,最多可以剪出an个小三角形,则a1=4,an+1=an+2.从而有
a1=4,a2=a1+2,a3=a2+2,……,an=an-1+2,
将上述n个式子左右两边分别相加,得到
an+1=2n+2,
于是,有a1996=2×1996+2=3994.
解法三与错解(解法一)的根本区别在于,an是n个点时所有剪法中剪出最多的小三角形的个数.
4.二十多年前,我来到深圳中学工作,教初一超常班,那时候市面上到处都是北京海淀区出的教学资料,上面有一道题:绝对值不超过100的全体整数之和是多少?答案为0.第二年该书再版,原作者把这道题改为:绝对值不超过100的全体有理数之和是多少?答案仍为0!殊不知,这一改就成了一道错题了!
下面请听我慢慢道来:
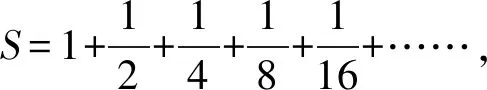
①

②

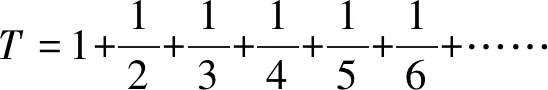
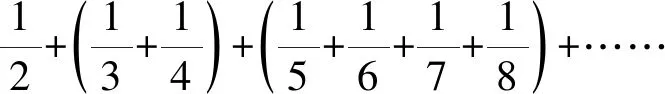
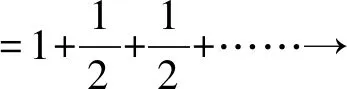


可见0 下面有点像变戏法: 由此得到 现在把将式③和式④左右两边对应位置上的数分别相加,得到 观察式③和式⑤,只是运算顺序不同(用了加法交换律),但是,左边却明显不相等,就是说,交换数的运算顺序,所得结果变了! 这是什么原因? 现在回到前面,绝对值不超过100的全体有理数有无穷多个,运算的顺序不同,其和就不一样.如果我们把“有理数”改成“实数”,那就更错了,因为实数是不可列的,根本无法相加!书的作者可能不知道黎曼定理,因此造成错解.这里,我们建议师范院校数学课本涉及内容可以更宽更广,但不必太深.




