关于Milosevic不等式的再研讨

郭要红

(安徽师范大学数学与统计学院 241000)

1 引言

设a,b,c,R,r,s,△分别为△ABC的三边长、外接圆半径，内切圆半径，半周长与面积，∑表示循环求和.

文[1]介绍了由D.M.Milosevic提出的如下不等式：

①

文[2]给出了不等式①的一个加强.

定理1在△ABC中，有

②

等号当且仅当△ABC为正三角形时成立.

对Milosevic不等式进行再研讨，本文得到不等式①的一个逆向不等式以及不等式②的一个加强.

定理2在△ABC中，有

③

等号当且仅当△ABC为正三角形时成立.

定理3在△ABC中，有

④

等号当且仅当△ABC为正三角形时成立.

2 三个引理

为证明不等式③与不等式④，先给出三个引理.

引理1[3]在△ABC中，有

∑ab=s2+4Rr+r2；

∑a2=2(s2-4Rr-r2)；

∑a3=2s(s2-6Rr-3r2).

引理2[4]在△ABC中，有

等号当且仅当△ABC为正三角形时成立.

引理3[5]在△ABC中，有

等号当且仅当△ABC为正三角形时成立.

3 主要结论的证明

利用引理1与abc=4Rrs，有

(b+c)(c+a)(a+b)

=(2s-a)(2s-b)(2s-c)

=2s(s2+2Rr+r2)，

根据半角公式与余弦定理，有

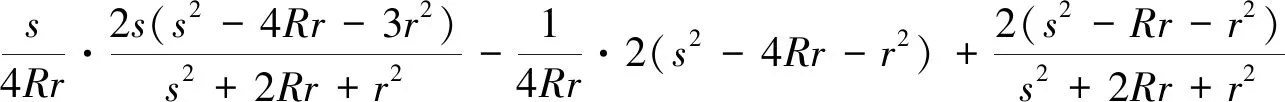
3.1 不等式③的证明

证明根据熟知的欧拉不等式R≥2r知

18R2-3Rr-2r2-16R2=2R2-3Rr-2r2

=(2R+r)(R-2r)≥0，

于是18R2-3Rr-2r2≥16R2，

⑤

⑤式等号成立当且仅当R=2r,即△ABC为正三角形时.

利用引理2与⑤式，有

由引理2与⑤式等号成立的条件知，不等式③等号成立当且仅当△ABC为正三角形时. 定理2得证.

3.2 不等式④的证明

证明由欧拉不等式R≥2r知

8R3-(4R3+6R2r+3Rr2+2r3)

=(4R2+2Rr+r2)(R-2r)≥0，

所以4R3+6R2r+3Rr2+2r3≤8R3，

⑥

⑥式等号成立当且仅当R=2r，即△ABC为正三角形时.

利用引理3与⑥式，有

由引理3及⑥式等号成立的条件知，不等式④等号当且仅当△ABC为正三角形时成立，定理3得证.

4 讨论

注意到

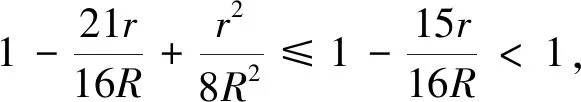
于是，我们得到不等式①的一个类似.

推论1在△ABC中，有

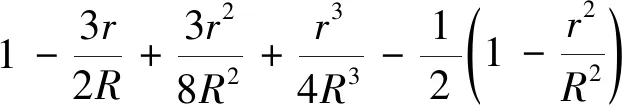
所以，不等式④是表不等式②的加强.