古希腊三大几何问题的近似尺规作图①
2020-04-13王淑红
蒋 迅 王淑红
(河北师范大学数学与信息科学学院 050024)
1 引言
尺规作图是初等几何教育中的一个课题.它对培养学生的几何想象能力起到了重要作用.在古代,尺规作图的研究曾经促成过多个数学领域的发展.一些结果就是为解决古希腊的三大几何问题而得到的副产品.对尺规作图的探索推动了对圆锥曲线的研究,并发现了一批著名的曲线.我们也知道,不是任何的几何图形都可以用直尺和圆规作出来的,其中最著名的就是古希腊的三大几何问题.尽管如此,人们还是尝试着用直尺和圆规作出尽可能接近目标的图形来.本文就介绍自古至今人们对古希腊三大几何问题的近似解法,特别是拉马努金(Srinivasa Ramanujan,1887—1920)的一个作图法和丢勒(Albrecht Dürer,1471-1528)的一个作图法.本文也将提及著名数学家陶哲轩(1975—)在其中一个问题上的讨论.
2 古希腊三大几何问题
所谓尺规作图,指的是只使用直尺和圆规经过有限次使用来作出不同的平面几何图形.这里,直尺必须没有刻度,无限长,且只能使用直尺的固定一侧.只可以用它来将两个点连在一起,不可以在上面画刻度.而圆规可以开至无限宽,但上面亦不能有刻度.它只可以拉开成你之前构造过的长度或一个任意的长度.
古希腊三大几何问题是早期希腊数学家特别感兴趣的三个问题.它们分别是:
三等分角问题:分任意角为三等分.
倍立方体问题:求作一立方体,使其体积等于已知立方体的两倍.
化圆为方问题:作一个与给定的圆面积相等的正方形.
下面我们分别介绍这三个问题的的发展历史和近似尺规作图.
2.1 三等分角
三等分角的尺规作图被旺泽尔(Pierre Wantzel,1814-1848)在1837年证明是不可能的.他是以代数方程理论为基础得到证明的.此后,人们对这个问题仍然兴趣满满.有些人力图给出其他证明或推广.这方面的一个著名结果是陶哲轩在2011年给出的几何证明.他的结果实际上证明了,任何n等分角都是不可能的,只要n不是2的幂.还有康奈尔大学数学教授卡恩(Peter J. Kahn)的一些工作.另一些人则在减弱限制条件下证明.这方面的尝试有二刻尺方法、折纸方法、连锁作图法、直角尺作图法、辅助曲线作图法等,或者对一些特殊角度作图.关于二刻尺方法和折纸方法,可见作者发表于《数学文化》杂志的文章“二刻尺作图的古往今来”.更多的是一些缺乏数学训练的业余数学爱好者们给出的大量尺规作图方法.他们声称旺泽尔的结果是错误的.有人把这些作图法收集起来,出版了书.这真是一件可悲的事情.而我们在这里要讨论的是在减弱结果的条件下的尺规近似作图.
三等分角的尺规近似作图相对于倍立方体和化圆为方来说是最容易的.我们可以反复四等分角来实现.这是基于下列的几何级数:
用这个方法作图,可以在有限步骤里对三等分角达到任意精度.以60°角为例,用这个数列的前三项得到的是19.6875°,用前四项得到的是19.9218756875°,误差只有0.078125°.注意即使是60°角,三等分角的尺规作图也是不可能的.类似地,可以用来作三等分角的级数还有一些,比如下面的几何级数:
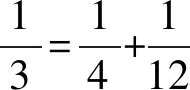
除了基于级数的作图法,也有其他达到不错精度的近似方法.
我们介绍德国中世纪末期、文艺复兴时期著名画家、雕刻家和数学家丢勒在1525年发表的一个作法.相信读者对他在艺术上的成就所知甚多,但其实他也是一位优秀的数学家,曾经写过关于几何学的著作《量度四书》,其内容主要是使用圆规、直尺的量度指南.而且他特别着重讲了几何学原理在建筑学、工程学和排版式编排设计中的应用.从他就可以看出西方艺术家早就认识到数学对于艺术创作的重要性.
梁元帝萧绎是个爱读书的人,常常让身边的人昼夜不停地为他读书,即使睡着了,他手里也还拿着书卷。而如果为他读书的人读错了或者故意漏读欺骗他,他就会马上惊醒——可以说,此人的确是个超级书迷了。
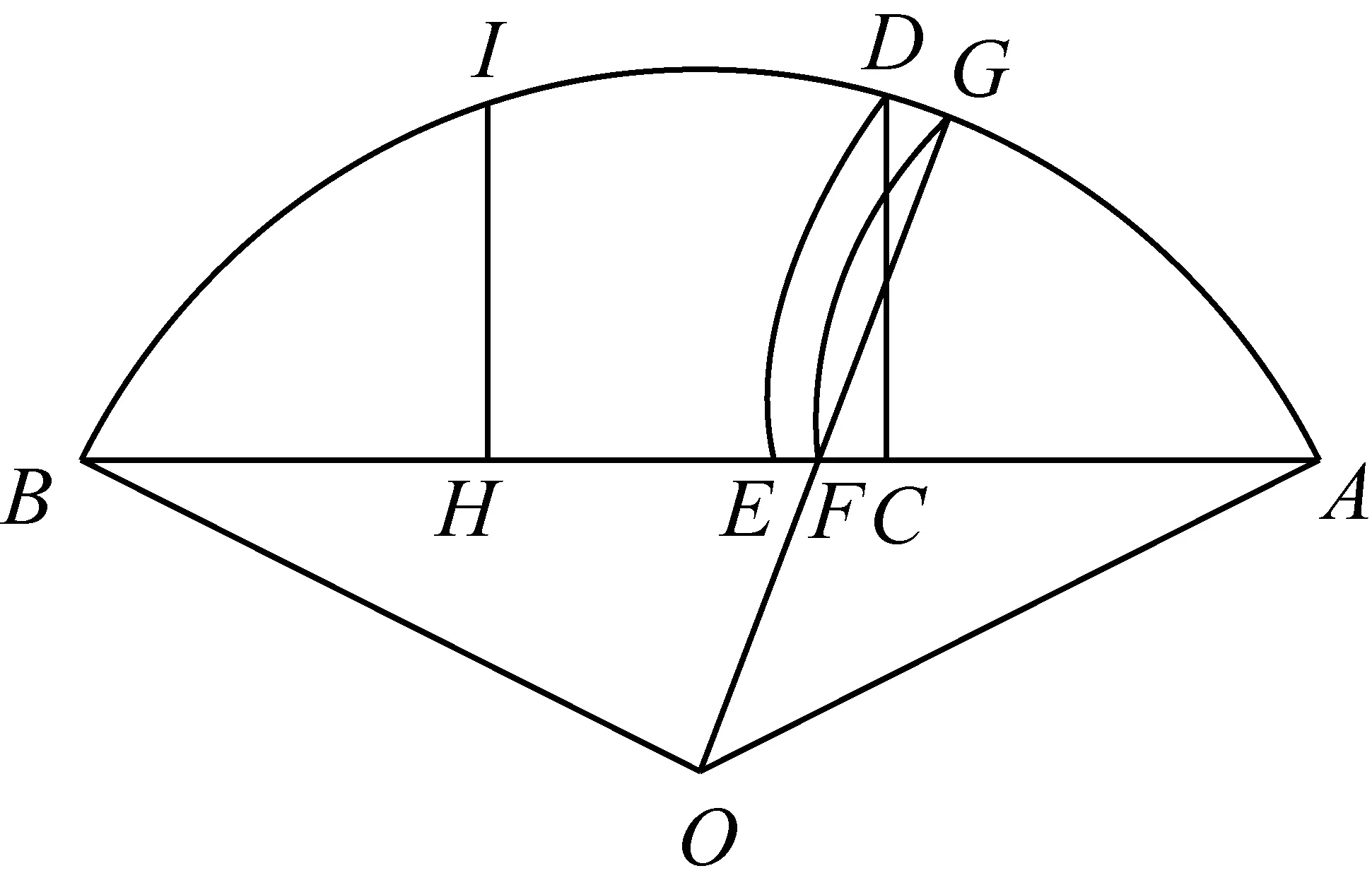
1966年,一位美国数学业余爱好者给出了一个只适用于小于90°的方法(当角度大于90°时,我们可以先减去一个90°的角来实现).他以为自己得到了一个完美的三等分角的尺规作图法,但其实是一个不错的近似方法.后来美国蒙塔纳州的一位程序员罗伊(Jim Loy)作了一些简化.我们介绍如下:
2.2 倍立方体
倍立方体问题最早是柏拉图给欧多克斯(Eudoxus,约前408-前347)、阿尔库塔斯(Archytas,前428—前347)和梅内赫莫斯(Menaechmus,前380—前320)提出的.当时提出时,柏拉图没有给出一个严格的问题描述.有一种说法是这些人用了一些工具作出来了.这迫使柏拉图明确地提出必须用“纯几何”的方法.另一种说法是他们给出的解答过于抽象而不具实际用途.还有一个相关的神话故事.关于这个问题,我们在《数学都知道2》第5章里介绍过.这里不再叙述.
倍立方体的尺规作图不可能性的证明是旺泽尔在1837年证明三等分角问题之不可能性时一起得到的.如果我们愿意减弱限制条件,那么这个问题也是有解的.比如,二刻尺、折纸、直角尺以及借助蔓叶线(Cissoid of Diocles)、蚌线(Conchoid)和费隆线(Philo line)等方法.在“二刻尺作图的古往今来”中,我们也介绍了倍立方体问题的二刻尺和折纸作图.在这里最值得一提的是阿尔库塔斯在公元前四世纪给出的在三维空间中的作图.他在那个时候就有了用曲线作旋转体的思想.
尽管这个问题有很深的历史渊源和有趣的神话故事为依托,尺规近似作图的例子却不多.这很可能是因为这些作图法都比较简单,不值得大数学家们下笔吧.我们选择1872年发表在《伦敦皇家学会会报》上的一个作图法.
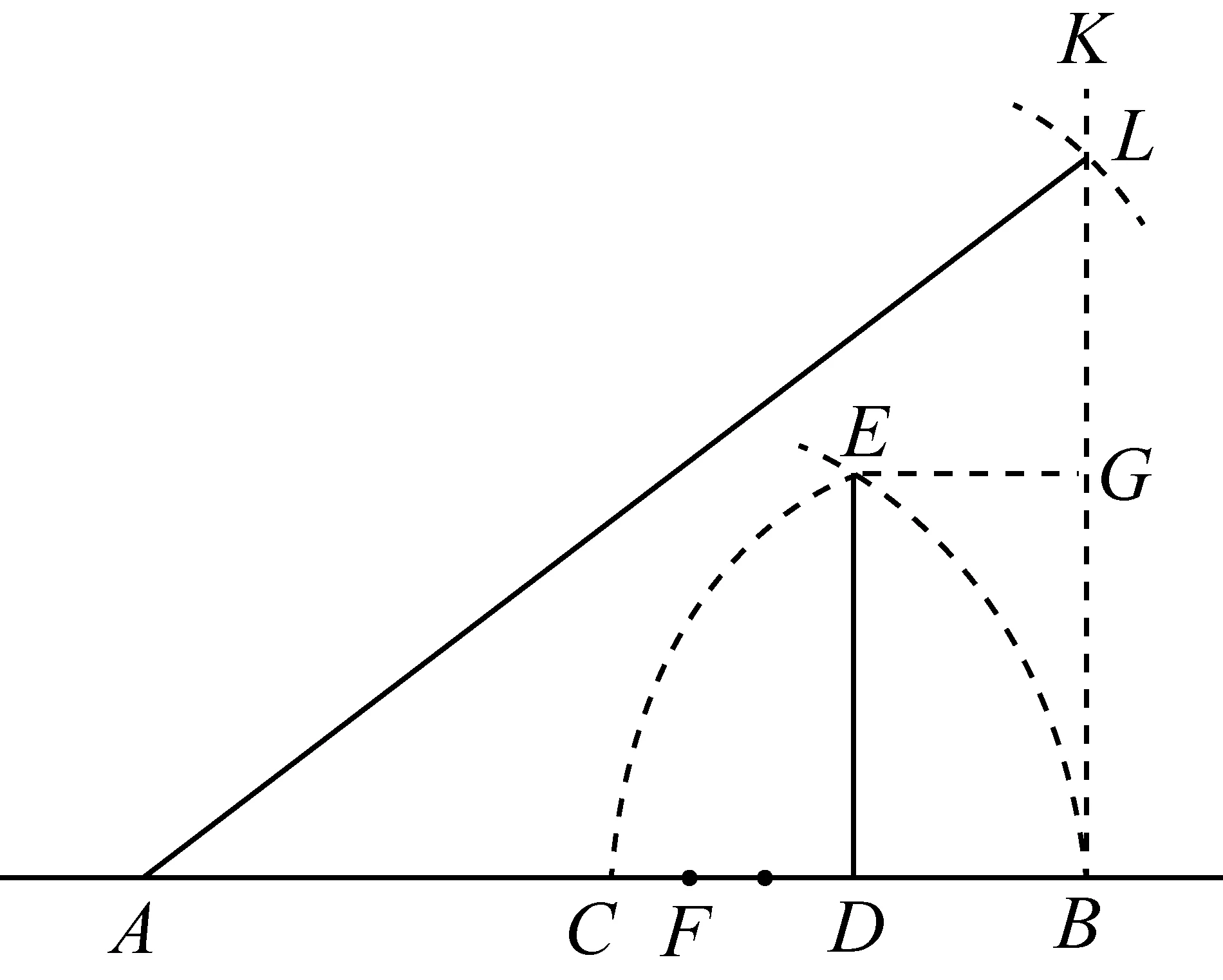
|BL|=|BG|+|GL|
≈3.77962646453,
V2=|AL|3≈53.9941419096.
1921年,《科学美国人》月刊发表过另一个作图法.2016年,一位德国人在维基百科上发布了一个非常棒的作图法.按照此人的方法,如果给定边长为十亿公里(光也要走55分钟!),那么体积加倍后的边长误差仅为0.2毫米,体积的误差为0.8立方分米(大约一升).
2.3 化圆为方
如果能够利用尺规化圆为方,那么必然能够从单位长度出发,用尺规作出长度为π的线段.化圆为方的尺规作图之不可能性的证明晚于三等分角和倍立方体.它是由德国数学家林德曼(Ferdinand von Lindemann,1852—1939)在1882年证明的.魏尔斯特拉斯(Karl Weierstrass ,1815—1897)在1885年推广了林德曼的结果.他们的结果被称为“林德曼-魏尔斯特拉斯定理”.
与三等分角和倍立方体问题不同的是,化圆为方不能用二刻尺和折纸方法实现.在西方甚至用化圆为方来比喻做不可能的事情.但借助其他工具化圆为方还是可行的,比如借助希比阿斯(Hippias of Elis,生于公元前460年左右)的割圆曲线(quadratrix of Hippias)、阿基米德螺线(Archimedean spiral)等.
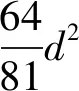
第一位对化圆为方表达兴趣的古希腊人是安纳萨哥拉斯(Anaxagoras,约前500-前428),但我们没有更详细的记载.希波克拉底(Hippocrates of Chios,前470—前410)研究了月牙面积问题(Lune of Hippocrates),希望由此解决化圆为方问题.正式提出化圆为方问题的是恩诺皮德斯(Oenopides of Chios,约前450年左右).但是直到1667年才有苏格兰数学家格列高里(James Gregory,1638-1675)开始试图证明这个问题是不可解的.二百多年后,这个问题才被林德曼最终解决.他证明了化圆为方和化方为圆都是不可能的.
在认识到化圆为方是不可能的之后,人们开始尝试用直尺和圆规来构造出近似等于π的线段来.1913年,英国数学家霍布森(Ernest William Hobson,1856-1933)给出了一个方法,近似到了小数点后四位(误差为 4.8×10-5).同年,印度著名数学家拉马努金给出了一个构造分数355/113的方法,从而将近似度提高到了小数点后六位(355/113 = 3.141592920353…).
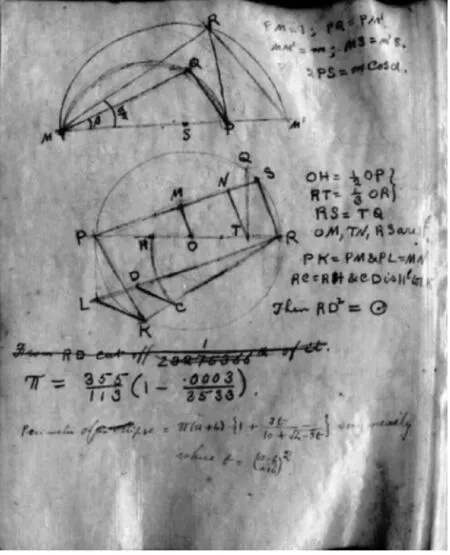
拉马努金笔记(1)拉玛努金笔记1,第54页.
1914年,拉马努金又发现了一个作图法能计算
这个结果将近似值提高到小数点后八位.这方面还有新西兰裔美国数学家奥尔兹(Carl Douglas Olds,1912—1979)、美国著名数学科普大师加德纳(Martin Gardner,1914—2010)和英国数学家迪克森(Robert Dixon,1947—)等.我们下面就介绍拉马努金的作法.
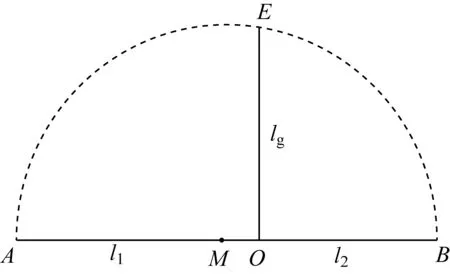
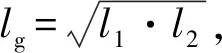
现在我们可以介绍拉马努金的方法了.
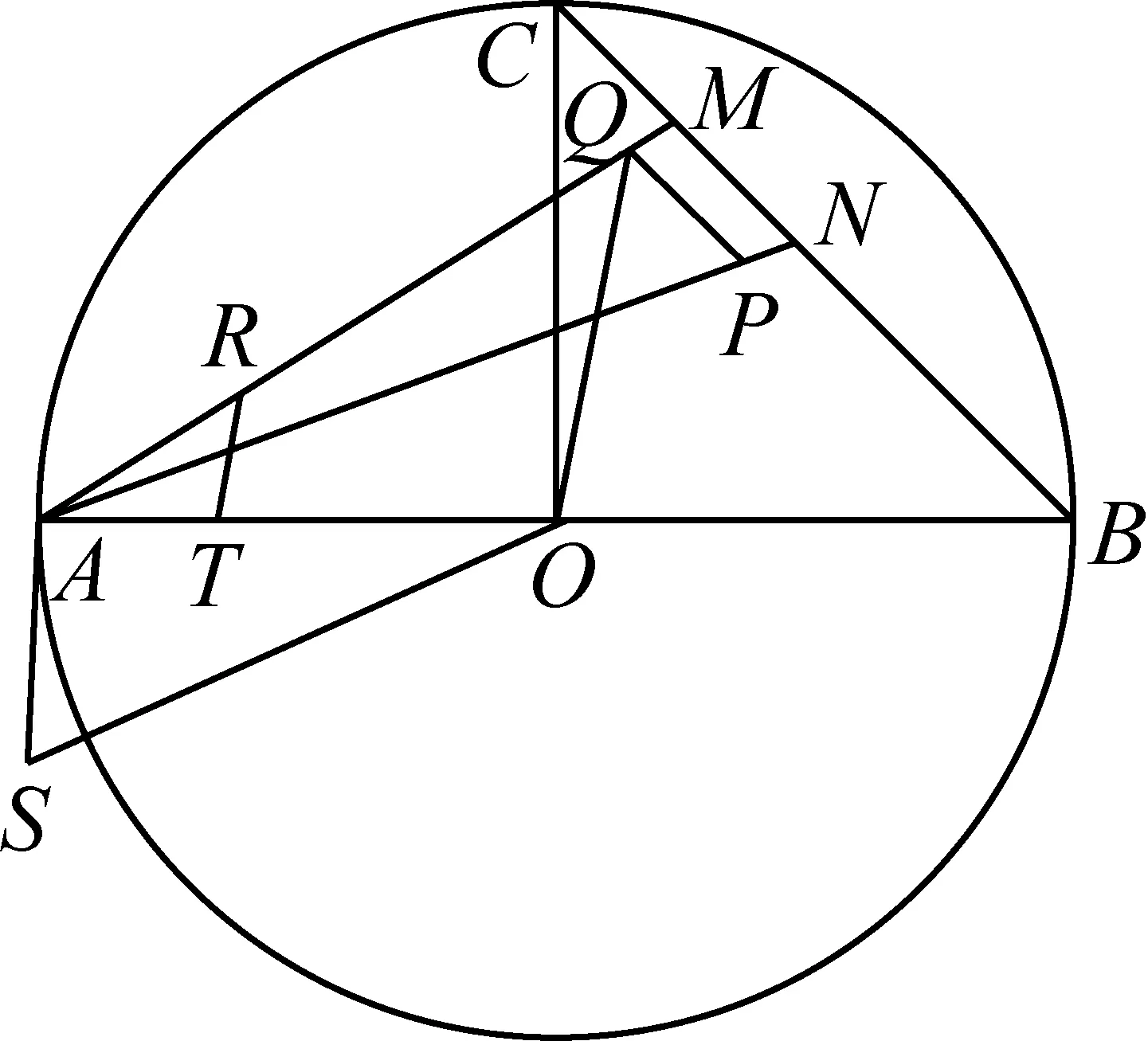
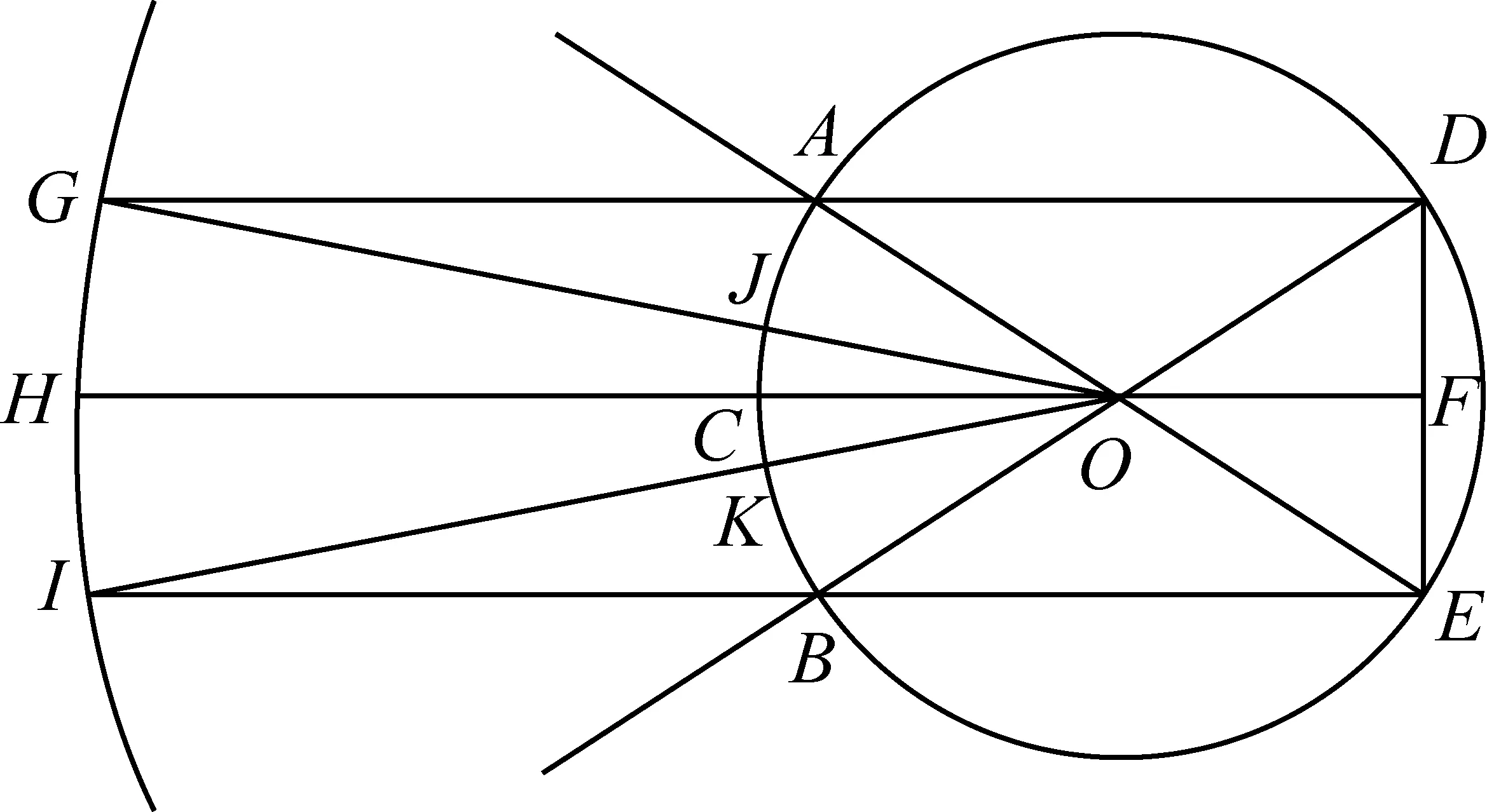
拉马努金的作图方法

连接点A和点M,同时连接点A和点N.在线段AN上取点P使得|AP|=|AM|.过点P作线段MN的平行线并交线段于AM点Q.连接点O和点Q并过点T作OQ的平行线TR交AQ于R.过点A作RT的平行线AS使得|AS|=|AR|,连接OS.拉马努金的构造到此为止.他声称线段OS和线段OB的几何平均大约等于圆周长的六分之一.
我们下面将继续作出一个正方形来,它的面积将近似于圆的面积.
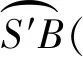
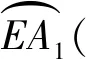
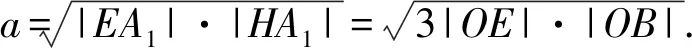
=3.141592652582641252…
这是一个什么概念的近似呢?拉马努金说:“当直径为8000英里长时,误差小于十二分之一英寸.”这大约就是2.1厘米.大师的思路是很精彩的.
3 结束语
除了以上三大不可能尺规作图问题外,还有很多几何图形不能用尺规作出.最著名的是正七边形.它是正多边形中第一个不能由尺规实现的平面几何图形.以下的n代表着不能由尺规作出的正多边形的边数:
7,9,11,13,14,18,19,21,22,23,25,26,27,28,29,31,33,35,36,37,38,39,41,42,…
事实上,总共只有31个已知的奇数边正多边形.有些正多边形即使能用尺规作出也是相当复杂.1900年前后,有人作出了正65537边正多边形,他的手稿装满一个大大的皮箱.这样的作法只有理论上的意义,没有实际应用的意义.
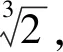
于是,对实数中的非规矩数如何近似就是一个现实的课题了.莫海亮在他的《圆之吻:有趣的尺规作图》中介绍了正五、七、九、十一、十九边形的近似作图.我们认为,即使对于不能用尺规实现的几何图形,尝试它们的近似作图也是一种挑战.
人们对完美情有独钟,但是有的时候近似也是一种美.
