由数学问题2268引发的研究

杨先义 赖源霞

(湖北省公安县第一中学 434300)

《数学通报》2015年10月号问题2268[1]：

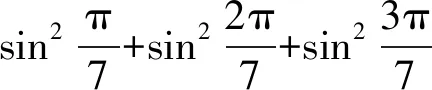
供题人柳冉同学给出的解答技巧性较强，过程曲折精彩．崔志荣老师在文[2]中从揭示问题的本质出发给出了另外一种解答，很有启发性，并在文末提出了2个猜想．黄盛清老师在文[3]中另辟蹊径，从方程的角度给出了又一个精彩解答，并在文末再次提出了能否将(1)式一般化的问题．本文首先给出一个更为直接的证明，然后将(1)式一般化，从而也证明了文[2]提出的猜想．

证明可证正弦的7倍角公式：

sin 7α=-64sin7α+112sin5α-56sin3α+7sinα．

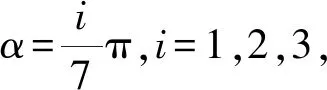
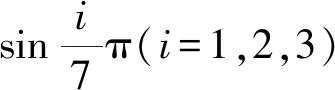
-64x6+112x4-56x2+7=0．

下面考虑一般情形．

我们有如下结果：

sin 2α=2sinαcosα，

sin 3α=-4sin3α+3sinα，

sin 4α=2sinα(2cos3α-cosα)，

sin 5α=16sin5α-20sin3α+5sinα，

sin 6α=2sinα(16cos5α-16cos3α+3cosα)，

sin 7α=-64sin7α+112sin5α-56sin3α+7sinα，

sin 9α=256sin9α-576sin7α+432sin5α-120sin3α+9sinα．

这些结果似乎表明α的奇数倍的正弦展开式才是sinα的函数，而sin(4n-1)α与sin(4n+1)α的展开式又有很大不同．来看一般情形，

令x=sinα，y=cosα，由平方关系，有

y2=1-x2，以下n为正整数．

一方面，由棣模弗定理，有

(y+ix)4n-1=cos(4n-1)α+isin(4n-1)α，

另一方面，由二项式定理，有

因为i2=-1，i3=-i，i4=1，所以，比较虚部得

显然这是一个关于x的4n-1次多项式，偶次幂的系数全为0，最高次的系数由各项的最高次系数合并得到：

=-24n-2，

x4n-3系数为

=(4n-1)24n-4，

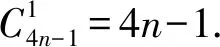
因此，上述多项式可表示为

f(x)=-24n-2x2n-1+(4n-1)24n-4x2n-2-…+(4n-1)，

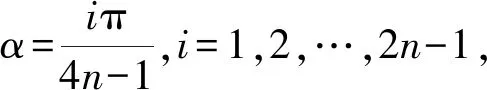
有sin(4n-1)α=0，

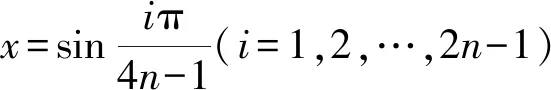
满足关于x的4n-1次方程f(x)=0，

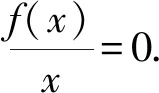
满足2n-1次方程

f(x)=-24n-2x2n-1+(4n-1)24n-4x2n-2-…+(4n-1)=0

由根与系数的关系，有

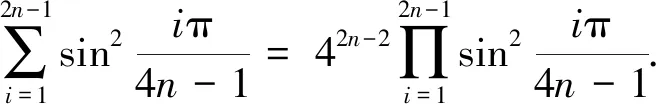
用同样的方法可得

sin(4n+1)α=24nx4n+1-(4n+1)24n-2x4n-1+…+(4n+1)x，

综上所述，我们得到

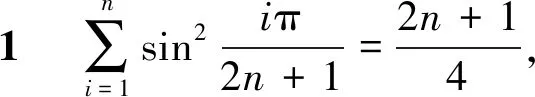
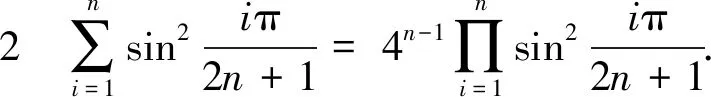
这样就完全证明了文[2]中的猜想1和猜想2.