2019年高校自主招生试题中的不等式问题

北京市十一学校

不等式是现代初等数学研究的中心,也是清华大学、北京大学等高校自主招生考试的热门考点和难点之一.仅2019年,在清华大学的自主招生及领军计划数学试题中出现3道不等式题目(共35道题目),清华大学的优秀中学生暑期综合营试题中出现1道不等式题目,在北京大学的三位一体招生数学试题中出现3道不等式题目(共20道题目),北京大学综合营中不等式题目更是占到文理科共7道题目中的3道.在其他高校的招生考试中,不等式题目也常有出现.今年,高校招生政策面临重大调整,“强基计划”完全取代了实行17年的自主招生政策,但基于选拔人才的初衷和“一校一策”的依托,预计题目类型不会发生重大改变,因此参考2019年的自招试题,对于备考和研究新的招生考试,依然有着很重要的意义.

自招考试中的不等式内容通常是多元均值不等式,有时会涉及柯西不等式和多元函数的最值问题,其难度不低于联赛一试中的不等式难度;从方法上看,配凑系数法和换元法的考察较为频繁,求导法、放缩法和数学归纳法也常有涉及,有时也经常与解析几何、函数与方程、三角函数、向量、因式分解等知识板块链接起来,范围很广,应予以重视.

例1(2019年上海交大自招考试) 实数a,b满足4a2-5ab+4b2=19,求a2+b2的最大值.

解答由题设,解得当且仅当a=b时取等号,即a2+b2的最大值为

例2(2019年浙大自招考试) 已知x2+y2+z2=1,求的最小值.

解答由常见不等式可知,解得当且仅当即时等号成立,即的最小值为-1.

评析这里实际考察的是对于基本不等式的配凑系数法的使用,在不知如何拆分时,可设1 =x2+λy2+(1-这里λ ∈[0,1],为求出的最小值,应有解得

例3(2019年上海交大自招考试) 已知x,y,z不全为0,求的最大值.

解答考虑到是求的最大值,不妨设x,y,z ＞0,而则当且仅当时取等.

评析这里可以用例2类似的方法得到所需配凑的系数.

例4(2019年清华自招与领军考试) 若正数a,b满足ab(a+8b) =20,则a+3b的最小值为( )

解答因此,a+3b ≥5,当且仅当即a=2,b=1时取等号.选B.

评析在上述方法中,由均值不等式和配凑系数法,不妨设需要配凑的系数为x和y,则:

这里x,y,要满足题目要求和均值不等式的取等条件,应使即化简可得解得或得到所需配凑的系数,即

例5(2019年清华自招与领军考试) 设则当(x,y)∈D时,( )

A.u的最小值为1 B.u的最大值为2

C.u的最小值为0 D.u的最大值为3

解答注意到与向量夹角的表达式很接近,令设两向量起点都在原点,则由于(x,y)∈D,即向量b的起点在原点,终点落在圆面x2+(y-2)2≤1 内,如图1所示.由于直线与圆x2+(y-2)2=1 相切,故〈a,b〉的范围是故选A和B.

图1

评析上述解法中,注意到与向量夹角的表达式之间的关系,可以为解决问题提供很好的帮助.类似的题目还有:

已知a,b,c,d ∈[2,4],求的最大值与最小值的和.(本题答案是.)

例6(2019年北大三位一体考试) 若a ＞b ＞0,且a3-b3=a2-b2,则a+b的取值范围为( )

A.(0,1) B.C.(0,2) D.前三个答案都不对

解答由a3-b3=(a-b)(a2+ab+b2),且a ＞b ＞0,有a2+ab+b2=a+b,即(a+b)2-(a+b) =ab,由可知,即因此选B.

评析在这里,通过因式分解达到化简约束条件的目的,之后再利用基本不等式构建起关于a+b的不等式,从而得到a+b的取值范围,这样的思路是非常重要的.

例7(2019年清华自招与领军考试) 设实数x,y满足x3+27y3+9xy=1,则( )

解答

因此有x+3y-1=0,或(x-3y)2+(3y+1)2+(x+1)2=0.

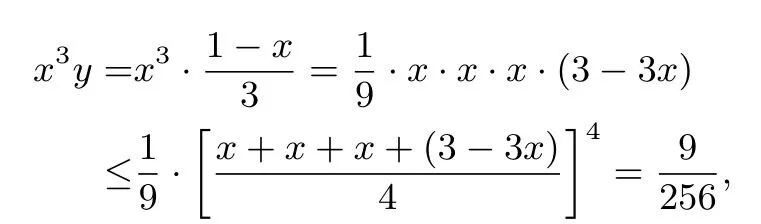
当且仅当x=3-3x即时取等号,此时

评析1.这里用到了因式分解

通过因式分解,得到了降次的目的,将约束条件简化.

例8(2019年北大综合营考试) 实数x,y,z满足x+y+z=x2+y2+z2=2,求xyz的取值范围.

解答解法一.由题,x+y=2-z,x2+y2=2-z2,由可知,因此另一方面,(z-1)2,故令f(z) =xyz=(z-1)2z=z3-2z2+z,则f′(z) =3z2-4z+1,令f′(z) =3z2-4z+1＞0,结合0≤则或因此,f(z) 在和上递增,在上递减,因此,(xyz)max=此时min{f(0),f(1)}=min{0,0}=0,此时{x,y,z}={0,1,1}.

解法二1,设a=xyz,则x,y,z是一元三次方程t3-2t2+t-a=0的三根,设f(t) =t3-2t2+t-a,则f′(t)=3t2-4t+1,令f′(t) =0,得列表如下:0.所以a=xyz=的最小值为0,最大值为

t(-∞, 1 3) 1 3(1 3,1) 1(1,+∞) f′(t)+0-0+f(t) ↗极大值↘极小值↗

评析解法一构建关于z的不等式求出z的取值范围,同时通过消元法将xyz化为z的函数,通过考虑函数在局部区间上的值域来解决问题:解法二注意到x+y+z,xy+yz+zx,xyz的关系,利用三次方程的韦达定理,构造起关于t的一元三次方程,从而求出a=xyz的范围.

为了获得z的取值范围,还可以通过韦达定理构造出一个关于t的一元二次方程,使其两根为x,y,通过考虑这个方程有解,获得参数z的取值范围:由题可有从而所以x,y是关于t的一元二次方程t2-(2-z)t+(z2-2z+1) =0的两根,应有Δ≥0,即(2-z)2-4(z2-2z+1)≥0,解得得到z的取值范围、实现消元后,还可利用均值不等式求出最大值,此方法的不足之处是无法求得最小值:

以两个约束条件为基础,可以得到三变量结构式的范围,这在近年北大清华的招生考试里常有出现,尤其是通过代数变形,建立起三变量对称式a+b+c,ab+bc+ca,abc,a2+等结构之间的关系,再通过构造不等式寻找范围.大家在解答这类题目时,务必注重代数变形、韦达定理构、造方程、统一变量、构造不等式等方法的应用.

例9(2019年北大综合营考试) 已知非负实数x,y满足求的最小值.

解答设显然取最小值时则问题转化为:已知非负实数a,b满足a+b=1,求的最小值.由柯西不等式,

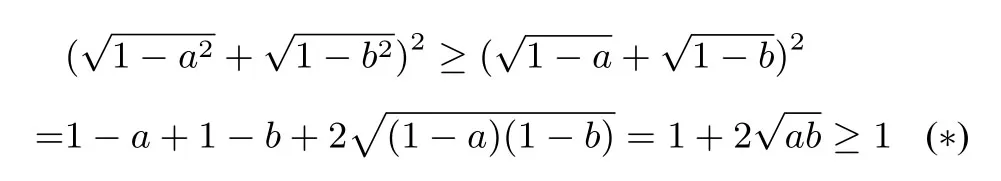
当且仅当ab=0时取等号,所以所求最小值为当或时取等号.

评析这里,换元的转换较为巧妙,这可以与下题建立起联系:已知求证:a2+b2=1.

事实上,12故等号必成立,因此即整理可得a2+b2=1.这是利用柯西不等式的取等条件证明不等式的经典例题,如果基础扎实且能联想起来,对于完成此题是非常有帮助的.此外,解答中柯西不等式的部分(*号标出),也可以按如下方法完成:1,则的最小值为( )

A.a2+b2+c2B.3(a2+b2+c2)

C.(a+b+c)2D.前三个答案都不对

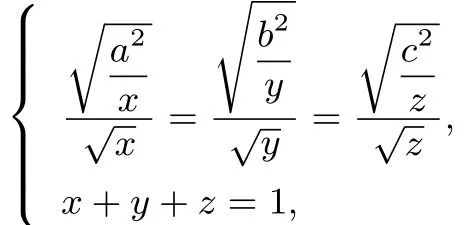
解答由柯西不等式,当且仅当即时取等号.这里,3(a2+b2+c2)≥(a+b+c)2,当且仅当a=b=c时取等号,且a2+b2+c2,(a+b+c)3与(a+b+c)2的大小关系取决于a+b+c的值,因此A,B,C 均不对,选D.

评析近年来,自招考试中对柯西不等式的考察有所加强,备考学生平常可以多做一些练习.

例11.（2019 北大三位一体考试）x,y,z为正实数,且x+y+z=1,则的最大值为( )

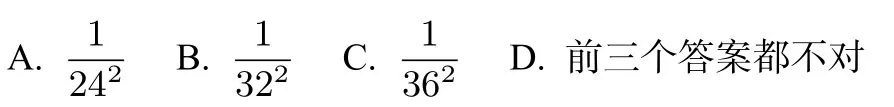
解答令

等号成立当且仅当ab=0.

例10(2019北大三位一体考试)x,y,z ＞0且x+y+z=将代入,可计算得故排除选项B,C;将代入,可计算得大于A,B,C 三个选项的值,故选D.

评析其实,取步长为0.00001的x,y,z值代入计算,可得最大值在0.0027 附近; 赋值得约为0.0023,较为接近.

本题用配凑系数法和拉格朗日乘数法等常规方法求解极其困难,但是可以很容易选出答案,在北京大学的自招题目中,常常出现这样的问题,即通过特殊值或合理推断排除选项,从而选出正确答案.实际上,这也是解决实际问题时证明或证伪的常用方法,可以达到考察学生综合能力、思辨能力的目的.这需要引起大家的重视.