解含绝对值问题的四个角度

广东省佛山市罗定邦中学

处理带有绝对值的不等式问题一般思路是利用绝对值的定义去绝对值,再通过分类讨论求得结果.本文在此基础上再介绍以下几种方法:利用绝对值不等式、最大值函数以及距离公式解决一类含绝对值的最值问题,供读者参考.

角度一通过绝对值定义去绝对值.

角度二绝对值不等式:|a|-|b|≤|a±b|≤|a|+|b|.注意到不等式的中间,可以通过选择“±”进行放缩使得不等式的一边出现定值.

角度三最大值函数最小值函数

角度四根据点P(x0,y0) 到直线l:Ax+By+C=0的距离公式:所以可以通过几何关系求解含绝对值的问题[1].

一、利用绝对值定义

例1已知函数设a ∈R,若关于x的不等式在R 上恒成立,则a的取值范围是____.

解析根据题意,对任意x ∈R 有:设原命题等价于g(x)max≤a ≤h(x)min.又由于

可得g(x)max=故答案为A.

总结:该解法的过程可总结为通过定义去绝对值,再分离出所求参数a.将原问题中的恒成立问题转化为最大最小值问题.

二、利用绝对值不等式

例2设f(x) =|log2x+ax+b|(a ＞0) 在区间[t,t+2](t ＞0) 上的最大值为Mt(a,b),若{b|Mt(a,b)≥1+a}=R,求实数t的最大值.

解析设函数g(x) =log2x+ax+b,显然g(x) 在[t,t+2]上递增.令Mt(a,b)=max{f(t),f(t+2)},其中f(t) =可知对任意b ∈R 都有Mt(a,b)≥1+a恒成立.所以min{Mt(a,b)} ≥1+a.又由于

两式相加可得:

总结本题通过绝对值不等式的放缩,巧妙的消去了参数a,b,最终只留下关于t的不等式.

例3(2015年佛山市数学教师解题大赛第11题) 已知f(x)=2x2+bx+c(b,c ∈R)的定义域为[0,2],记|f(x)|的最大值是M,则M的最小值为____

A.1 B.2 C.3 D.4

解析据题意即有根据绝对值不等式得到两者组合可得:M的最小值为1,故选A.

总结上面的解法利用了三次绝对值不等式,前两次消掉未知量“c”,最后一步消掉未知量“b”使得不等式的一边出现常数.特别注意的是,“=”是否成立.

经验证,当b=-4,c=1时,等号成立.针对该问题,题干所给区间是[0,2],为何选择0,1,2 这三个特征点来求M的范围呢？如果上面的“=”不成立,必然要选择其他的特征点来求解.而其根本的原因在于对图像的理解,所提供的二次函数在区间[0,2]上单增、单减或先减后增.通过绝对值处理后,其取得最大值的可能情况是两个端点及顶点的位置.根据对称性,假设该函数的对称轴在x=1 处.再通过“=”是否成立来验证.

例4已知a,b,c ∈R,且对任意x ∈R 恒成立,求的最大值.

解析设f(x) =acos2x+bsinx+c,令x分 别为:0,可得:根据绝对值不等式:

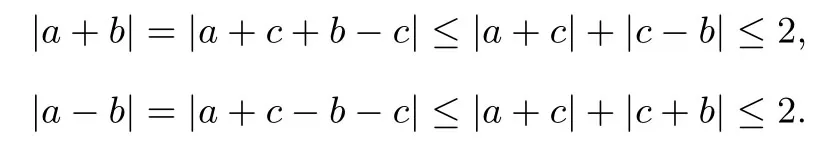
显然|asinx+b|max=max{|a+b|,|a-b|}≤2.|asinx+b|的最大值为2,当a=2,b=0,c=-1时,等号成立.

总结本题的一大难点在于特殊点的选择,读者可结合例2思考一下,是否可以选择其他的特征点求解,选择特征点的一般策略是什么？

三、利用最大最小值函数

例5已知函数f(x) =ax2+bx+c(0),记M(a,b,c) 为|f(x)|在[0,1]上的最大值,若求的最小值.

分析由|b|≥2|a|可知,该二次函数的对称轴无论该函数开口方向如何,函数f(x) 在区间[0,1]上单调,所以

解析根据分析可知:M(a,b,c)=max{|f(0)|,|f(1)|}.根据最大值函数的定义:

总结本题与例2相比,本题所涉及的函数单调性确定,所以最值必在端点处取得.且在本题中引入了最大值函数,结合绝对值不等式求得最小值.另外,本题的解法将参数a,b,c用f(0),f(1) 表示,读者可绕过该步骤,直接放缩.

例6已知方程

有三个根x1＜x2＜x3,若x3-x2=2(x2-x1),求实数a的值.

解析令根据最大值函数的定义:

原方程等价于max{f(x),g(x)}=ax+2,由-2x ≥得:由此可得:

因题设提及的方程有三个根,所以三个根的分布是第一段一个,第二段两个.由可得再由得到再由x3-x2=2(x2-x1) 得到2x1=3x2,即有所求a的值为

总结本题是最大值函数的逆向运用,通过最大值函数,将原有的绝对值问题转化为分段函数,通过分类讨论求出对应的根.

例7(2016年4月浙江省普通高中学业水平考试第18题) 设函数若对任意的正实数a和实数b,总存在x0∈[1,2]使得f(x0)≥m,求实数m的取值范围.

分析对任意的正实数a和实数b,总存在x0∈[1,2]使得f(x0)≥m,等价于min{max{f(x)}} ≥m.即当f(x) 在区间[1,2]上的最大值取到最小时仍不小于m时,上条件成立.

解析设函数存 在[1,2]使得f(x0)≥m.则有f(x)max≥m,又因为g(x) 在x ∈[1,2]上递减,所以f(x)max=max{f(1),f(2)}.

令M(a,b)=max{f(1),f(2)},其中f(1) =|2-a - b|,f(2) =|1-2a - b|,所以M(a,b)≥m对任意a ＞0,b ∈R恒成立,所以min{M(a,b)} ≥ m.又由两式相加可得:

总结通过上面的分析,对于加绝对值的函数,首先要选择关键点,利用关键点表达出所求的参数;再利用绝对值不等式进行放缩或利用最大值函数进行转化.

四、利用绝对值的几何意义求解

例8若函数f(x) =|asinx+bcosx-1|+|bsinxacosx|(a,b ∈R)的最大值为11,求a2+b2的最大值.

解析利用绝对值不等式:

构造直线:l1:ax+by=0,l2:bx - ay=0,点P(sinx,cosx),则有h(x) 表示点P到直线l1,l2距离之和的倍,其中l1,l2是过原点且互相垂直的直线,点P在单位圆上运动,点P到直线l1,l2距离分别为d1,d2,显然有利用基本不等式:所以故所以a2+b2的最大值为50.

总结第一步的放缩使得后面构造的直线过原点,大大地简化了后面的计算.

五、练习

4.已知函数f(x) =ax2+bx+c(0),当x ∈[0,1]时,|f(x)|≤2,求a的最大值.

答案提示:利用最小值函数.