基于协整理论的新疆消费水平实证研究

林 杉

(西安财经大学 陕西 西安 710100)

一、绪论

(一)选题的背景和意义

本论文通过建立一个符合社会主义市场经济特色和新疆地区发展特色的宏观经济模型，全面描述国民经济各领域简单的相互关系及相互影响。本文主要针对居民消费模块进行研究，通过协整检验理论，建立误差修正模型和向量自回归方程体系，这是年度宏观经济模型的重要组成部分。

二、新疆居民收入与消费协整关系的实证分析

(一)数据来源与说明

本文对新疆维吾尔自治区1994-2014年间宏观经济中的消费模块进行实证分析，主要针对消费与收入的关系进行研究，试图通过协整分析来判断收入与消费是否存在长期稳定的均衡关系。由于城镇居民和农村居民的收入消费函数存在较大的差异，故本文将居民消费分为城镇居民消费和农村居民消费两部分。

本文的数据来源于历年的《中国统计年鉴》。原始数据为1994-2014年新疆城乡居民收入与消费数据，将其剔除价格因素的影响。本文选取的统计变量有城镇居民人均可支配收入(YUR)、农村居民人均纯收入(YRR)、城镇居民人均消费支出(CUR)、农村居民人均消费支出(CRR)。由于各变量数据不全都是平稳的，为增强其平稳性，并消除可能存在的异方差现象，我们对选取的数据进行取自然对数处理，处理后上述变量分别设为LYU、LYR、LCU、LCR，对数变化不会改变原变量之间的协整关系。

(二)协整理论与误差修正模型的实证分析

1.平稳性检验(单位根检验)

本文基于单位根检验原理，利用Eviews6.0软件采用ADF方法对各变量及其差分变量进行单位根检验，其检验结果如下表1。

表1 各变量及其差分变量的单位根检验统计表

由表1的结果分析知，上述所检验的变量均为非平稳变量，即均有单位根的存在，故需对各变量进行差分并继续利用ADF法进行检验差分后各变量的平稳性。

2.协整关系的检验

根据依据上一节变量的单位根检验结果发现，在5%的显著水平下，LYU与LCU、LYR与LCR均为I(1)变量，由于同阶单整变量之间可能存在协整关系，故在检验协整关系时只需要检验LYU与LCU、LYR与LCR的协整关系。构造的协整方程具体如下：

(1)城镇居民消费与收入的潜在协整方程为：

LCU=-0.225384+0.996167LYU

t值：(-2.506993)(100.1782)

(2)农村居民消费与收入的潜在协整方程为：

LCR=0.061892+0.965713LYR

t值：(0.229353)(28.18165)

δt=LCR-0.061892-0.965713LYR

(3)误差修正模型(ECM)

通过软件拟合得到误差修正模型及其相关检验量和拟合指标如下：

ΔLCUt=0.003706+0.954634ΔLYUt-1.191605ecmt-1

(0.313335) (9.183232) (-5.0165)

此时得到残差是否自相关检验的结果与滞后期的结果如表2所示：

表2 误差修正模型残差自相关检验结果

显然，直到滞后5期的残差自相关检验结果都表明残差是不相关的，因此上述误差修正模型是合理的。

上述误差修正模型显示，城镇居民的消费短期波动一方面受到收入的短期波动影响，影响程度为0.954634，但并不受到消费和收入差分滞后期的影响，因此这种影响是没有滞后效应的。城镇居民的消费短期波动另一个影响就是反应在误差修正模型的修正项ECM中。对于两个变量的误差修正模型来说，误差修正想系数一定显著为负，从而实现偏离均衡的调整机制，其系数反映了变量波动偏离长期均衡时的调整速度与能力。就本文的实证结果而言，新疆城镇居民的误差修正指数为-1.191605，相对于短期波动的系数而言，调整速度和力度相当强烈。

三、居民消费向量自回归模型(VAR)体系的构建

(一)模型变量的设定

本章具体就消费、收入、价格以及金融的关系利用向量自回归的理论建立相应的VAR模型体系，所选取的内生变量有城镇居民人均消费(LYU)、农村居民人均消费(LYR)、城镇居民人均可支配收入(LCU)、农村居民人均纯收入(LCR)、城镇居民消费价格指数(LCPIU)、农村居民消费价格指数(LCPIR)。

(二)模型的构建

1.单位根检验

表3 各变量的单位根检验结果表

由表4-1结果分析知，上述的两种价格指数变量均含有单位根，即为非平稳变量。进一步检验非平稳变量的一阶差分的平稳性可得：在1%的显著水平下，两个变量都为一阶单整变量，即I(1)变量。结合上一章的单位根检验结果知，LYU、LCU、LCPIU均为I(1)变量，LYR、LCR、LCPIR也为I(1)变量，这满足协整关系的前提条件。

2.协整检验

表4 城镇的VAR模型各个标准与滞后期的关系

表5 农村的VAR模型的各个标准与滞后期的关系

注：*表示该信息指标下应该选择的阶数

上一章中对协整关系的检验采用的方法是EG两步法，这种方法只适用于单方程的协整关系的检验，而本章的两个模型中均含有三个变量，故不能继续采用EG法进行检验，本章采用Johansen和Juselius的特征根迹检验(trace检验)和最大特征值检验两种方法进行检验。JJ法不仅检测出变量之间是否存在协整关系，而且能够确定出协整变量的个数。具体检验结果如表6、表7所示：

表6 城镇消费体系中各序列协整检验的结果

注：**表示在1%的显著水平下拒绝原假设

表7 农村消费体系中各序列协整检验的结果

注：*表示在1%的显著水平下拒绝原假设

由表3、表4知，在1%的显著水平下，变量LYU、LCU、LCPIU三个变量之间存在协整关系，且只有一个协整向量；在1%的显著水平下，变量LYR、LCR、LCPIR、三个变量之间也存在只有一个协整向量的协整关系，这为VAR模型建立的合理性提供了前提。

3.VAR模型的构建

(1)城镇居民消费VAR(1)模型：

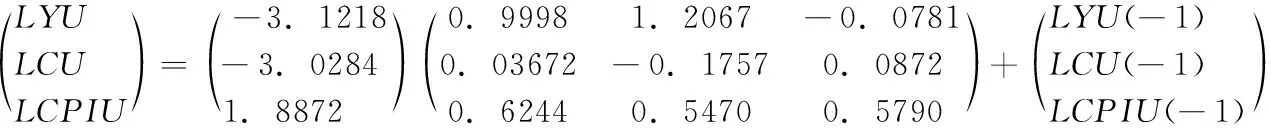
(2)农村居民消费VAR(3)模型：

模型整体检验结果如表8。从整体检验结果来分析，两个模型的AIC和SC值都很低，拟合的效果也都很好，故可以进行预测。

表8 居民VAR模型的整体检验结果

(三)VAR模型的模拟与预测

1.对历史数据的模拟

为了更加客观地描述模型的预测能力，本文将先采用“样本内预测”的方式，针对1994-2014年进行“预测”，依据上一节求解的VAR模型，对各变量的残差进行分析，得出相对误差表。即对已知的历史数据进行预测，得出的预测值与我们所知道的真实值进行比较，得出模型的预测误差，预测的相对误差(预测误差/实际值)如表9所示，由此可评价模型的预测能力，这样做的好处是不需要花费更长的时间等待新数据的产生。

表9 居民消费VAR模型预测绝对误差表 (单位：%)

由表4-8知，城镇居民人均消费的最大预测误差约为0.963%，城镇居民人均可支配收入的最大预测误差约为1.078%，城镇居民消费指数的最大预测误差约为1.039%。同理，由表4-9知，农村居民人均消费的最大预测误差约为0.855%，农村居民人均纯收入的最大预测误差约为1.906%，农村居民消费指数的最大预测误差约为3.171%。由此可见，除了城镇居民人均消费的预测效果低于农村居民人均消费之外，其它两项指标的预测最大误差都是城镇消费体系的指标较低。总体来说，所有指标的预测的最大误差均在5%以内，因此预测误差整体满足要求，这说明模型的短期预测能力很高，可以进行预测。

四、结论与建议

可以采取措施来改善人民的消费观念的差异，逐步改善农村经济结构及农村设施，大力发展旅游业，丰富农民收入来源，充分提高农民的收入，同时，加大对农业发展的扶持力度，降低农民对农业生产投资的风险度。为进一步促进城镇居民消费水平的提高，政府可放宽买房、买车的限度，完善社会保障体系及信用体系，提高中低层收入者的工资水平，促使人们将储蓄转化为消费。