超声波在水中衰减的频率效应及其对脉冲回波的影响

程明，潘勤学，肖定国，徐春广，刘然，杨超

（北京理工大学 机械与车辆学院，北京100081）

0 引言

衰减是超声波在介质中传播的重要特性。一方面，可以利用超声波的衰减特性表征金属材料的成分、表征乳液和悬浮液颗粒的粒径和浓度、表征生物组织特征等［1-4］；另一方面，超声衰减会对基于界面反射原理的脉冲反射式超声无损检测方法的检测性能产生不利影响。对于脉冲反射式超声无损检测方法，超声脉冲的中心频率是决定其检测能力的关键参数，它决定着常用的脉冲反射法测厚检测的测量分辨力和脉冲反射法C扫查成像检测的横向分辨力，在高频超声检测及超声显微检测中，这种尤为明显［5］。采用超声脉冲回波法进行检测时，要判断检测能力，需要考虑超声波传播的衰减特性，分析反射回波的中心频率和信号波形；此外，分析超声传播的衰减特性可以预测回波频率和信号波形。目前，针对超声衰减的研究主要集中在30 MHz以下的领域，对高于100 MHz的超声衰减研究较少［6-11］。

本文针对水耦脉冲反射式超声，研究了高频超声波在水中传播的衰减规律及其对脉冲超声波中心频率的影响。在分析超声波在介质中传播的衰减机理以及衰减模型的基础上，使用带平面声透镜的标称中心频率300 MHz的高频超声换能器和表面光滑的陶瓷块反射体进行实验，研究超声波在水中传播衰减的频率特性，以及对反射回波脉冲中心频率的影响。

1 超声波传播衰减的距离及频率效应模型

1.1 超声波传播衰减的距离效应模型

超声波在液体中传播的衰减主要分为由传播介质特性决定的吸收衰减、散射衰减，以及由声源特性引起的扩散衰减。在研究声波与传播媒质特性关系时，仅需考虑前两类衰减；计算声波传播损失时，必须全面考虑这三类衰减因素。计算衰减系数时，如果衰减斜率与频率成线性关系，则可以考虑通过对数谱线性拟合来计算衰减斜率［7，12-13］。

通常，由传播介质的特性决定的超声衰减遵从指数衰减规律［14-16］，即沿声波传播方向的振幅A与传播距离x的关系为

式中：A0为初始振幅；α为衰减系数。

目前，实验已经验证了超声波在介质中传播时声压与振幅随距离的指数变化的关系。R.Martinez等人［17］在19.7℃和25℃的纯水中，分别用脉冲回波法和透射法实测了1 MHz超声波随传播距离的衰减情况，结果如图1（a）所示。

图1（a）说明，超声回波信号的幅值随传播距离的变化呈现指数规律衰减。但是，该实验观察的是脉冲信号的衰减，从换能器发出的脉冲波形是宽频的，带有多个频率成分，脉冲超声波传播一定距离后的幅值衰减并不仅仅是1 MHz频率成分的幅值衰减，而是多个频率成分幅值衰减后叠加后的结果。因此该实验并不能准确描述不同频率的衰减情况。如图1（b）所示，在相同传播距离下不同频率的反射回波具有不同的衰减系数，频率越高衰减越大［16，18］。

1.2 超声波传播衰减的频率效应

Thorp［11］认为衰减系数是频率的函数，并总结了衰减系数与频率之间关系的公式，但是该公式只适用于低于5 MHz的超声波。

Dingguo Xiao等人［19］设计了脉冲回波法实验来研究单个频率成分的幅值衰减规律。如图2所示，反射体表面回波的中心频率明显低于透镜回波的中心频率，且表面回波的幅值远低于透镜回波。由此可知在水中传播的超声波具有衰减现象，并且频率越高，衰减速率越快。

该实验及Perter B的实验关于不同频率成分衰减不同的结论，说明了使用式（1）来描述含有多个频率成分的脉冲超声信号的衰减是不准确的，对于特定的频率，振幅随距离的衰减规律呈指数关系，但是对于特定的传播距离，不同频率成分的振幅随频率的衰减规律尚不清楚，有待研究。

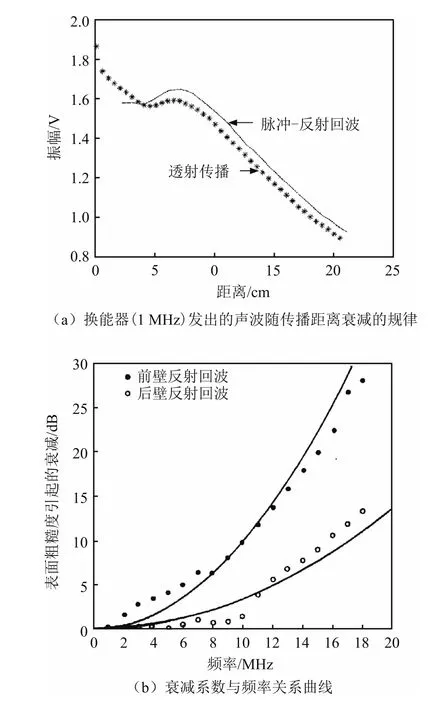
图1 幅值随距离衰减和衰减系数随频率变化曲线

1.3 超声波传播衰减的距离效应和频率效应综合模型

本文提出了将不同位置的反射回波进行傅里叶变换以取得各个频率成分的幅值，然后计算其与初始位置的幅值之比的方法，来求得对应频率衰减系数和多频率成分超声波的衰减谱，由此得到脉冲超声波在传播时声波幅值与传播距离、频率的综合模型。

由上述研究结果可知：频率固定时，超声波的传播衰减随距离增大而增大，且遵从指数衰减规律；传播距离固定时，超声波的传播衰减随频率增大而增大。超声检测中常用脉冲波（脉冲波是宽频超声波），因此分析其衰减规律时应综合考虑距离效应和频率效应，衰减模型式（1）中应考虑衰减的频率效应，即衰减系数α是关于频率f的函数。因此式（1）可扩展为含有频率和距离两个变量的公式。式（2）描述了频率为f的超声波分量的衰减规律。

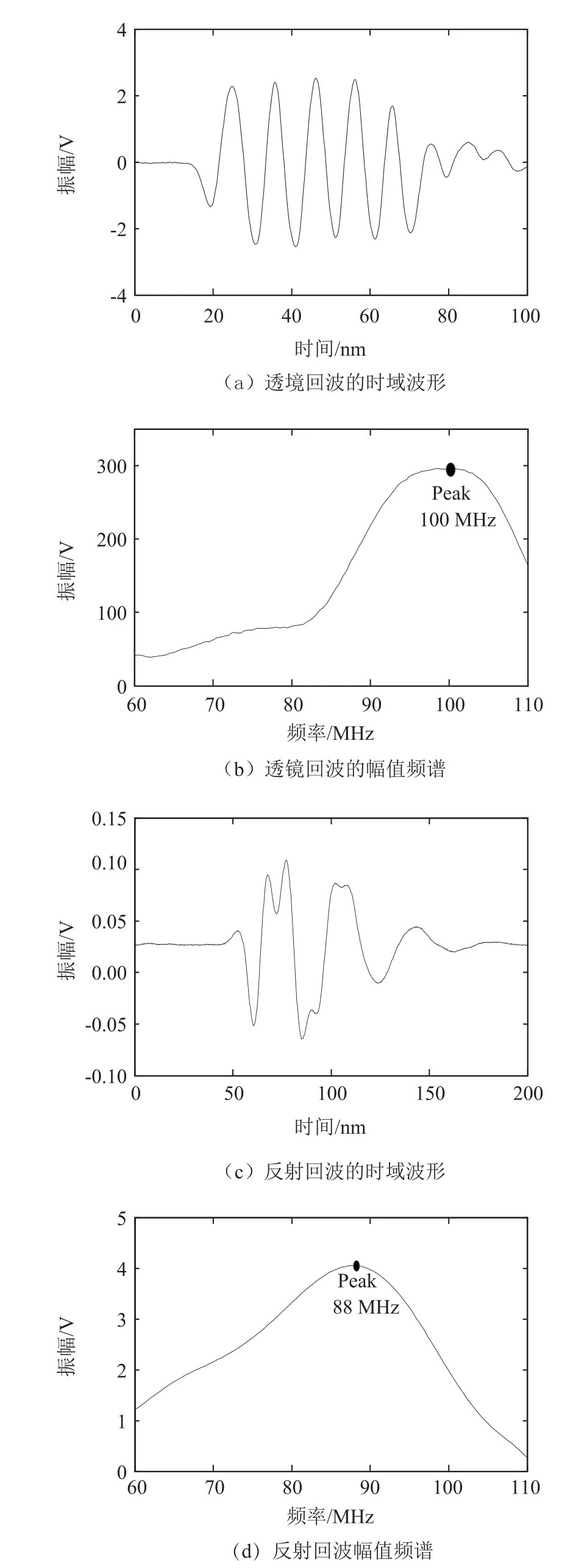
图2 透镜回波与反射体表面回波的时域频域图

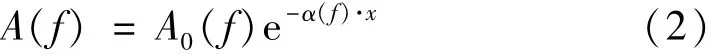
式中：A（f）为传播衰减后的声波幅值；A0（f）为初始传播位置的声波幅值；α（f）为衰减系数频谱。使用脉冲回波法检测时，声波在水中的传播距离x为传感器到反射体距离的2倍。

将式（2）移项并取对数后可得

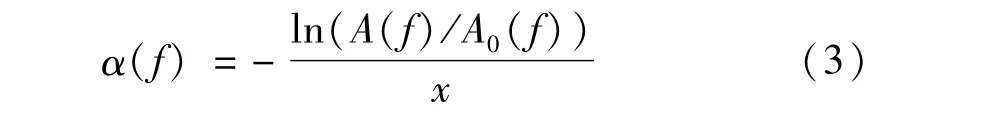
2 脉冲超声波在水中传播衰减规律的实验研究方法及衰减系数频谱测量方法

实验通过采集和分析经不同反射距离传播的脉冲超声波信号，研究超声波传播衰减与传播距离和超声频率的关系。在水中传播的信号振幅衰减系数会随温度变化，但是该误差影响很小，可以忽略［14］。

利用高频超声显微镜实施实验研究，如图3所示，高频超声换能器用于激发和接收脉冲超声波，回波脉冲信号经脉冲收发仪放大后由数字示波器采集记录，利用显微镜的运动控制系统使换能器沿Z轴方向位移，实现反射距离调整，利用陶瓷试块作为声波反射体。

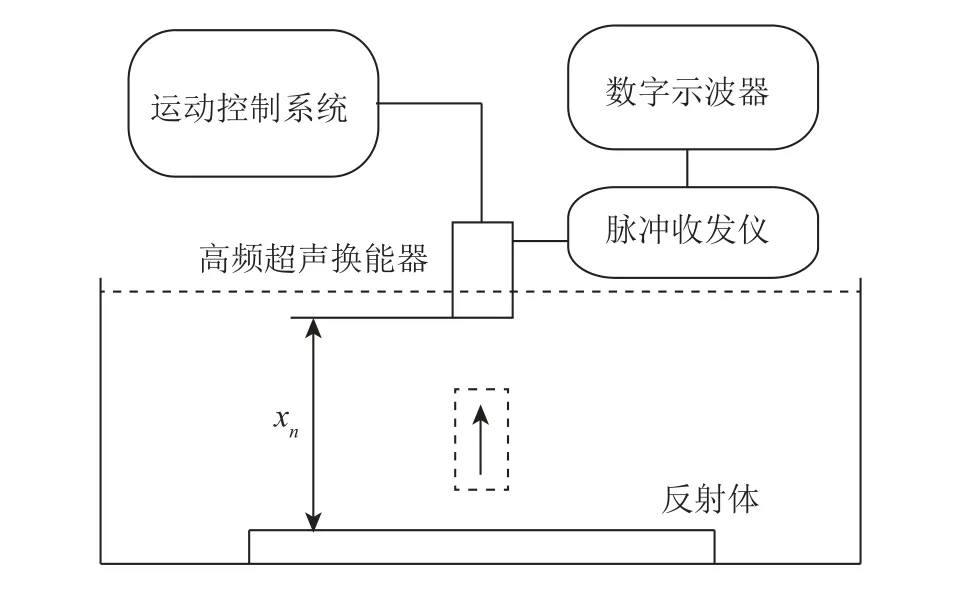
图3 脉冲超声波在水中传播衰减的实验系统

图3 中，高频超声换能器从离反射体表面极近的位置x0处向远离反射面的方向移动，直到几乎观测不到反射回波的位置xn处，采集不同反射距离xi处（此时超声脉冲的传播距离是2xi）的反射回波信号，得到如图4（a）所示的脉冲回波时域波形。

使用快速傅立叶变换（FFT）的方法对反射回波数据进行离散傅里叶变换，其实数部分反映回波脉冲不同频率成分的幅值强度，即回波脉冲的幅值频谱，如图4（b）所示。

对不同反射距离xi（i＝0，1，2…n）处的回波信号进行傅里叶变换，计算xi（i＝0，1，2…n）处反射脉冲不同频率成分fj（j＝1，2，…，n）的幅值Ai（fj）与初始位置x0处该频率成分幅值A0（fj）的比值，可得幅度衰减与距离及频率的关系数据，如表1所示。

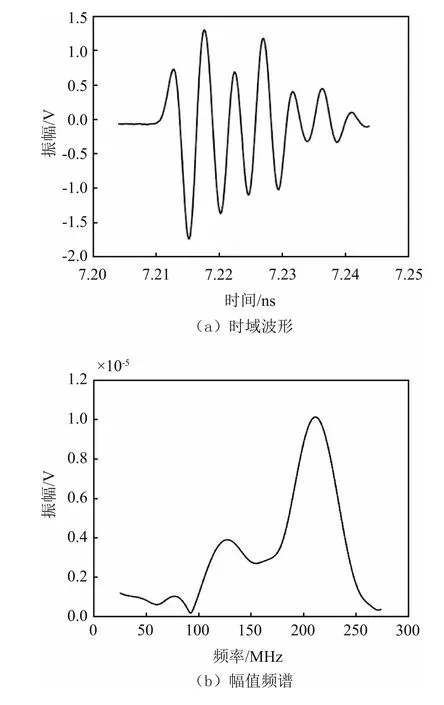
图4 反射回波脉冲的时域波形与幅值频谱

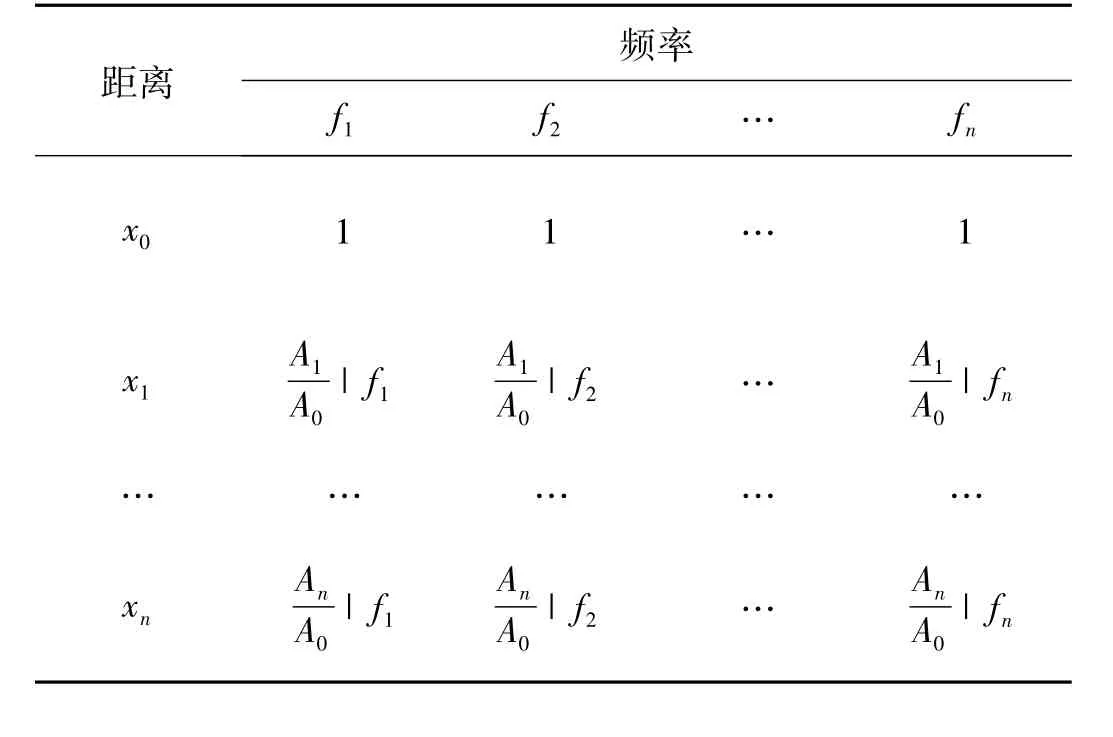
表1 幅值衰减与距离及频率的关系

按列分析表1中的数据，可以得到回波脉冲信号不同频率分量fj（j＝0，1，2，…，n）的幅度随传播距离xi（i＝0，…，n）衰减的规律，即xi-Ai（fj）／A0（fj）（i＝1，2，…，n）曲线，该曲线代表某一特定频率fj（j＝1，2，…，n）分量的振幅衰减比随传播距离的变化规律。根据已有的超声波传播衰减机理和模型，该曲线应为指数曲线，符合式（1）。若不同频率下的xi-Ai（fj）／A0（fj）（i＝1，2，…，n）曲线呈现规律性变化，则说明衰减系数与频率f有关，式（2）指数规律衰减模型成立。

按行分析表1中的数据，可以得到回波脉冲在不同传播距离xi（i＝1，2，…，n）下幅度衰减程度随频率变化的规律，即fj-Ai（fj）／A0（fj）（j＝1，2，…，n）曲线，该曲线代表某一特定反射距离xi处振幅衰减比随声波频率的变化规律，进一步计算可得到该传播距离下的衰减系数频谱α（f）。根据已有的超声波传播衰减机理和模型，不同反射距离下得到的衰减系数频谱应是相同的。

根据上述分析，可建立基于脉冲反射传播的超声波传播衰减系数频谱测量方法：采集相距x的两个反射距离下的超声脉冲回波信号，并进行傅里叶变换，计算这两个信号各频率分量的幅值比，得到fj-A（fj）／A0（fj）（j＝1，2，…，n）曲线，再根据式（3）即可算出衰减系数频谱如式（4），这种方法相较于连续正弦信号激励法将更加快捷方便。

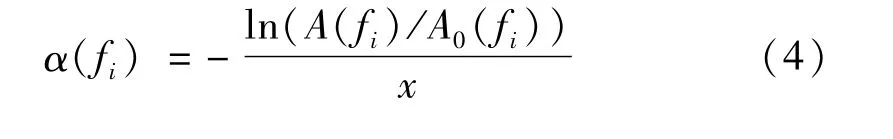
3 实验结果及分析

3.1 超声传播衰减的距离效应和频率效应实验

如图5所示，从超声换能器入射到水中的超声波信号在频域上的表现不是中心频率为300 MHz的理想波形，实际中心频率为211.21 MHz。本文主要研究水中频率的衰减，所以先不关注传感器内部的频率衰减。按照上文拟定的实验方案对标称中心频率为300 MHz的高频脉冲超声波在水中传播的衰减情况进行测量。

选取x0＝0.5 mm为参考反射距离，该反射距离下测得的反射回波脉冲信号如图5所示，该脉冲信号的峰峰值幅度为0.2 V，中心频率为115.40 MHz。

由于反射回波各频率成分的幅值在25～250 MHz范围内比较清楚，所以在该范围内实测衰减的距离效应和频率效应。

通过移动超声换能器，得到不同的反射距离处的回波信号，测得反射距离x为0.9，1.9，2.9，3.9 mm时的反射回波波形如图6（a）所示，从图中可以看出，随着反射距离的增大，反射信号的幅度明显减小，幅度随传播距离增大按指数规律衰减，如图7（a）所示。根据反射体表面回波的频谱可以看出，反射体表面回波相对于初始位置反射体表面回波有明显的幅值衰减和频率左移现象。

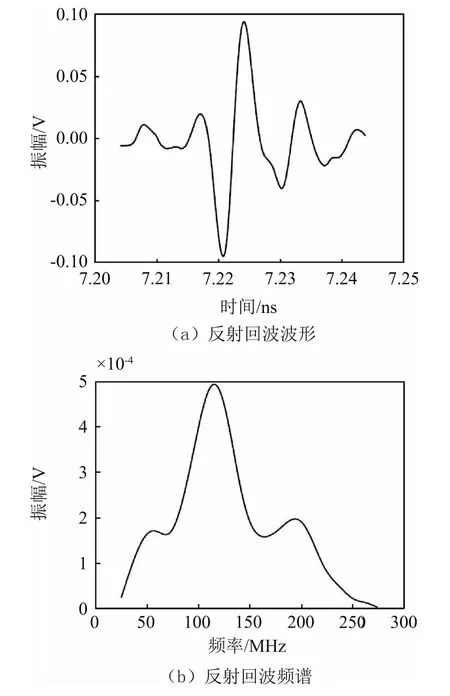
图5 反射距离x0＝0.5 mm位置时反射回波时域波形及其频谱

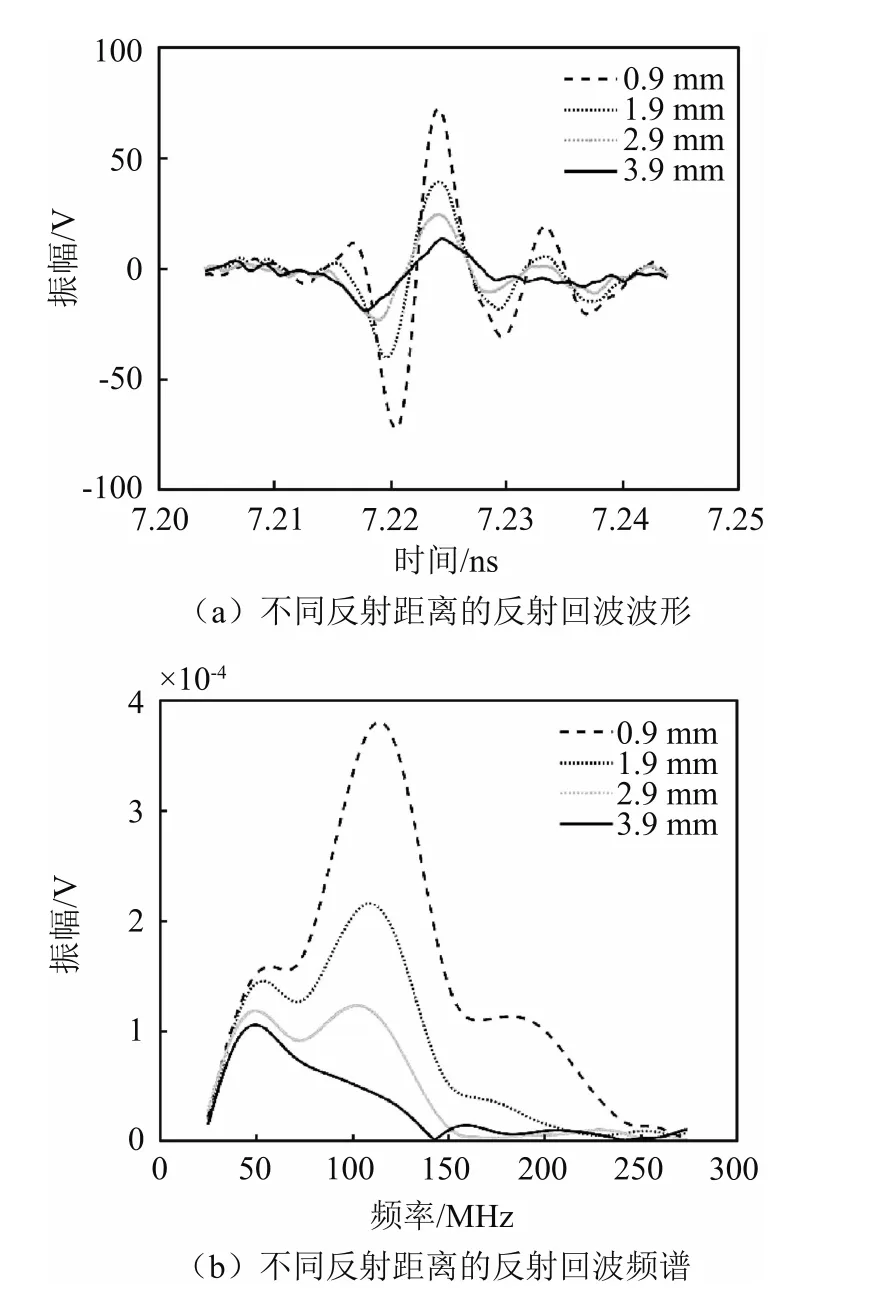
图6 脉冲超声的部分时频域波形

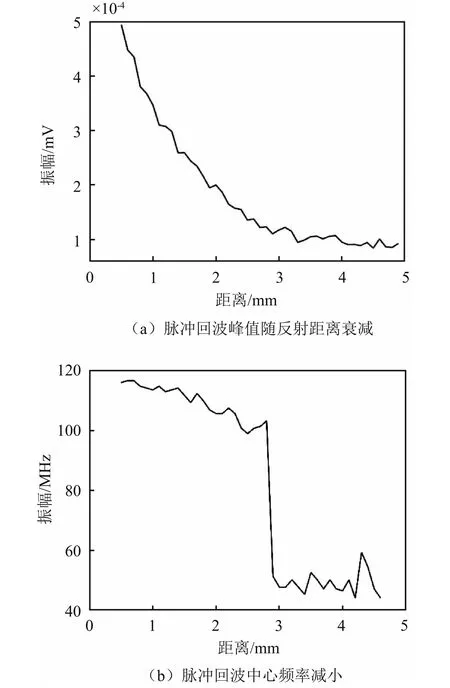
图7 脉冲超声传播的距离效应和频率效应

图6 （b）展示了在不同反射距离下反射回波脉冲信号的幅值频谱，可以看出，随着反射距离的增大，反射脉冲信号的中心频率明显减小，其规律如图7（b）所示，反射脉冲的中心随传播距离增大而变小的现象是由于超声波的衰减具有频率相关性，即脉冲超声波中的高频分量比低频分量衰减更大的效应导致的。

3.2 距离效应和频率效应的衰减规律分析

3.2.1 距离效应衰减特性及其表征模型

根据不同反射距离脉冲回波的幅值频谱，对4个频率分量f为109.25，139.77，151.18，182.49 MHz的幅值随反射距离衰减的情况进行计算，对数据拟合得到距离衰减曲线，结果如图8所示，图8（a）用绝对幅值减小表示超声传播距离衰减效应，图8（b）用相对幅值减小表示传播距离衰减效应。可以看出，对于所有的频率，超声传播的距离衰减效应呈现明显的指数规律。幅值A与距离x间呈现明显的指数衰减关系，如图8（a）所示；幅值比A／A0与距离x也呈现明显的指数衰减关系，如图8（b）所示。曲线可用式（1）进行描述，说明经典的超声波衰减模型虽然只考虑了衰减的距离效应，但表征特定频率超声波的传播距离衰减是正确的、可用的。对于特定频率超声波传播，通过分析或实验获得衰减系数α（f），即可用式（1）表征其距离衰减。

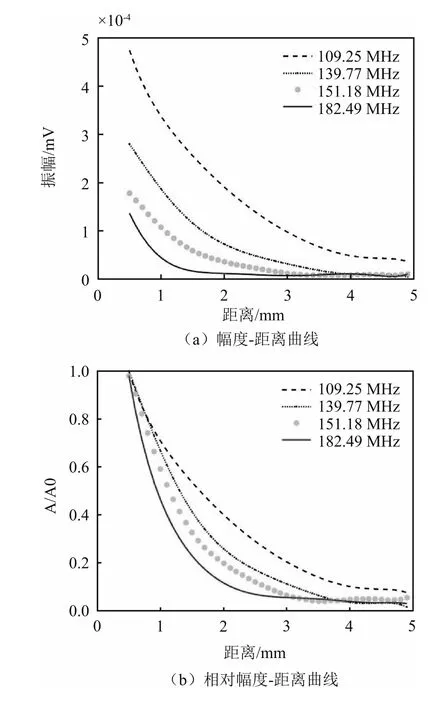
图8 超声传播衰减的距离效应

3.2.2 频率效应衰减特性及其表征模型

根据换能器初始位置x0和不同距离xn处对应的频谱图数据来计算衰减系数频谱α（f）。

根据不同反射距离脉冲回波的幅值频谱，对4个反射距离2.4，4.4，8.0，9.8 mm处的反射回波进行分析，计算幅值衰减随频率的变化情况，对数据拟合得到频率衰减曲线，结果如图9（a）所示。曲线本质上是特定反射距离下超声传播衰减系数随频率变化的规律，本文称其为超声传播衰减系数频谱α（f）。可以看出，不同反射距离下测得的超声传播衰减系数频谱规律基本相同，频率越高，衰减系数越大。计算传播距离x对应的α（f）并进行插值处理，得到超声波的衰减系数谱模型，如图9（b）所示。

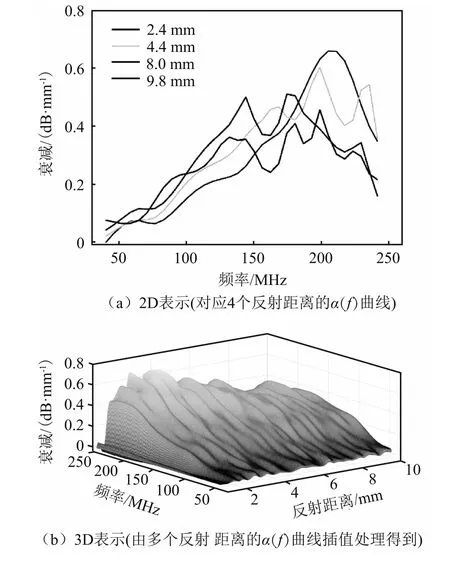
图9 超声传播衰减系数频谱

按照上文提出的基于脉冲反射传播的超声波传播衰减系数频谱测量方法测得实验数据，并使用MATLAB对上述曲线进行模型拟合，即可得到对应特定反射距离的超声波传播衰减系数频谱表达式。使用中值滤波函数（medfilt1）来处理异常峰值，并使用smooth函数进行平滑处理，处理后的数据与原数据相比没有其他明显变化。如图10所示，不同反射距离下的α（f）曲线具有相同的趋势，把每个频率对应的不同距离处的衰减系数进行平均处理，得到衰减系数的平均值数据点曲线。

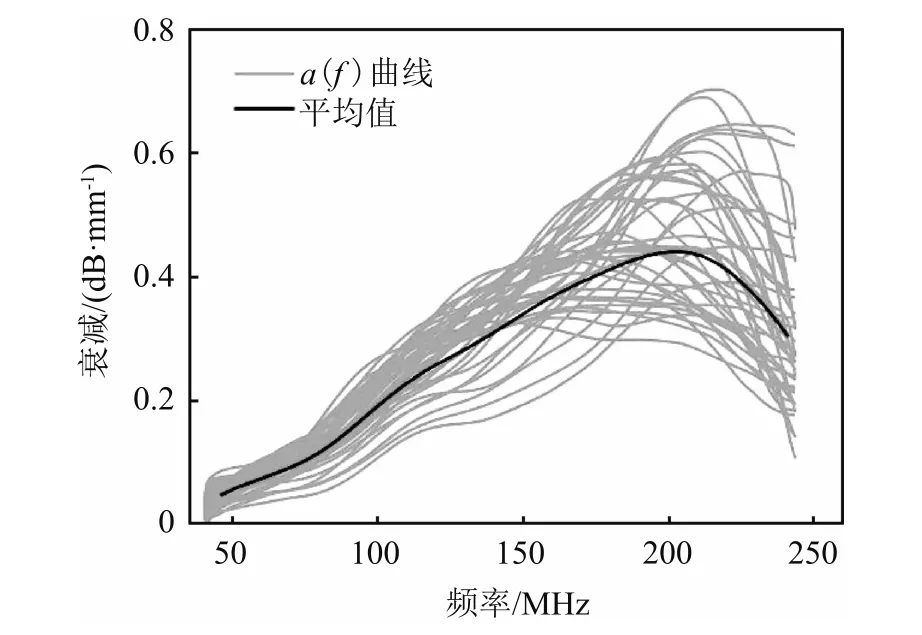
图10 原始α（f）数据曲线与平均值曲线

如图11所示，采用2次高斯模型对平均值数据点进行曲线拟合。

图11 原始数据点和2次高斯拟合后的α（f）曲线

平均值数据点拟合公式为

式中：f为频率，MHz。

数据点大都在拟合曲线附近，证明采用2次高斯模型能够较好地表征超声传播衰减系数频谱。

实验结果和分析表明，特定频率超声波的传播衰减与传播距离呈指数关系，同时，超声波传播的衰减系数随超声波频率而变化，超声波的传播衰减，特别是无损检测中常用的脉冲超声波传播衰减应该使用综合了距离衰减效应和频率衰减效应的模型进行表征，即

式中：a1，b1，c1，a2，b2，c2均 为 二 次 高 斯 拟 合参数。

4 结论

通过分析不同距离下反射脉冲回波的傅里叶变换结果，研究了超声波在水中传播时幅值衰减与传播距离与超声频率之间的关系，总结了超声波在水中传播的衰减规律。得到了以下结论：

1）特定频率的超声波分量的幅值衰减与距离呈现指数衰减规律，证明可使用傅里叶变换的方法来研究多频率成分脉冲超声波的传播衰减问题。

2）高频成分具有更大的衰减系数，因此随着传播距离的增大，脉冲超声波中幅值最大的分量的频率逐渐减小，即脉冲超声波的峰值频率减小，如图7（b）所示，反射距离从0.98 mm变化到2.9 mm时，脉冲回波的峰值频率从103.14 MHz减小到了51.27 MHz。水浸脉冲超声反射法是超声无损检测实践中最常用的方法，脉冲超声波的不同频率成分在水中传播时的衰减系数不同，高频成分衰减快，低频成分衰减较慢，因此，经一定距离传播衰减后，脉冲回波的峰值频率会变低，即实际检测频率比换能器的标称频率要低，在考虑水浸脉冲超声反射法的检测灵敏度和检测分辨力时，应注意由于超声衰减的频率效应引起的脉冲超声回波峰值频率降低的特点。

3）超声波在水中传播的距离衰减系数和衰减系数频谱可以通过本文的研究方法进行实测，首先测量不同反射距离下脉冲超声波在水中传播的反射回波，然后对其进行傅里叶变换，计算不同反射距离下各频率分量幅值与参考距离下对应频率分量的比值，即可得到特定频率声波的距离衰减系数以及衰减系数频谱。