一种基于格子玻尔兹曼前向模型的GPU并行加速荧光扩散断层成像的方法

吴焕迪，严壮志，岑星星

上海大学 通信与信息工程学院，上海市，200444

0 引言

荧光扩散断层成像技术（Fluorescent Diffuse Optical Tomography，FDOT）具有无创、定量、灵敏度高、成本低等优点，已成为医学计算中一种强力的分子成像技术，在癌症诊断、药物机理研究、脑功能成像方面具有巨大的潜力[1-2]。通常选择基于辐射传输方程（Radiative Transfer Equation，RTE）或扩散方程（Diffusion Equation，DE）模型求解FDOT。前者是一种复杂的积分微分方程，用于描述光在生物组织等介质中传播的精确模型；后者是前者的一阶球谐简化模型。尽管许多研究人员致力于缩短RTE和DE的计算时间，然而即使是处理小尺寸图像，求解RTE或DE模型也仍然不能满足动态成像的要求[3]。

FDOT的求解方法通常比较耗时。因此，迫切需要一种新颖有效的传播模型。格子玻尔兹曼方法（Lattice Boltzmann Method，LBM）与FDOT的协同发展有可能解决快速成像问题。LBM是一种基于宏观和微观之间的介观尺度模型的偏微分方程数值求解工具，具有计算稳定、物理含义明确、并行结构简单、易实现的特点。

目前LBM已经广泛应用于流体力学和热辐射，但是在光学传输领域LBM还是一个新兴、极具前景的方法[4-5]。例如PATIDAR等[6]提出了基于LBM的辐射传输方程瞬态解并且利用二维组织模型进行了验证；ZHANG等[7]提出了一种用基于格子玻尔兹曼方法求解前向模型的方法，与利用COMSOL方法求解相比，该方法的求解速度比用COMSOL快2.3倍。但是目前为了获得准确的目标位置和丰富的成像信息需要提高重建图像的空间分辨率，上述方法在CPU上处理大规模的LBM计算速度较慢，不足以满足快速成像的需求。由于LBM与GPU并行化的契合性十分高，二者的结合能解决空间分辨率和计算速度之间的矛盾问题。

因此我们提出了一种基于格子玻尔兹曼前向模型的GPU并行加速荧光扩散断层成像的方法。此方法通过构建基于LBM的RET的前向模型，把LBM的碰撞、迁移、边界处理过程在GPU上并行计算，可以大大提高求解速度，之后利用代数重建技术（Algebraic Reconstruction Technique，ART）计算重建结果，最终把计算结果可视化。为了验证本方法的可行性和加速性能，我们还进行了数值仿真实验和物理仿真实验。通过实验，从耗时和准确性方面证明了所提方法的可行性。

1 基于格子玻尔兹曼方法的荧光扩散断层成像模型

首先，从BGK-Boltzmann方程的离散形式推导，对速度、时间、空间都进行离散化。由于微观粒子无时无刻不做着非规则的运动，因此微观粒子的运动速度方向可以是无穷多个；同样的，粒子的离散速度也可以是无穷多个。离散速度定义为一个有限的集合，即{e0,e1,e2,...,en}，为离散速度的个数。同样的，离散分布函数集合则为{f0,f1,f2,...,fn}，α为当前离散速度方向，α=0,1,...,n。离散BGK形式为：

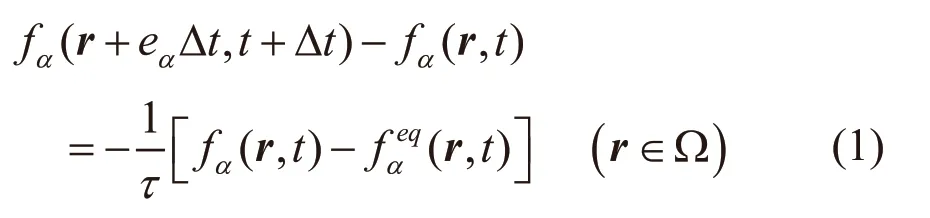
其中r定义为在空间Ω中的位置，t定义为时间，△t定义为时间间隔，往往一个△t对应LBM的一次迭代，为松弛时间，fa(r,t)为当前离散速度方向的分布函数，为当前离散速度方向的平衡的分布函数。同时离散的辐射传输方程为：

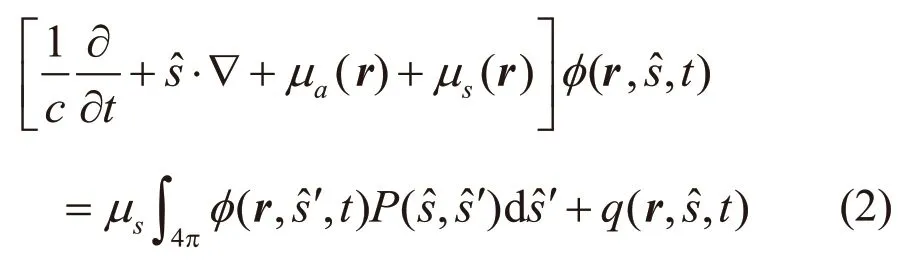
其中c为光子在生物组织中的传播速度，表示方向。表示在t时刻、在空间r处的方向为s的辐射强度。μa(r)和μs(r)分别表示在位置r处的吸收系数和散射系数。表示从方向s到s'的光子传播的散射相函数。为光源场的光强分布函数。

为了把格子玻尔兹曼方程和辐射传输方程构建至光传播的离散模型，首先对式（1）两边都乘以v，其中v表示光子的频率，再把辐射传输模型中的光源与LBM中的平衡态分布函数做类比，可以得到：

再把辐射强度密度函数和速度分布函数做关联，h为普朗克常数，可以得到：

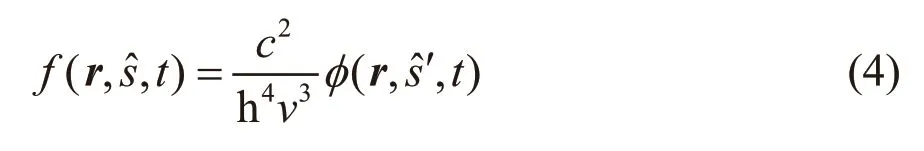
通过上述的关联，把式(3)和(4)代入式(1)，最终可以得到基于LBM的RTE离散化模型：

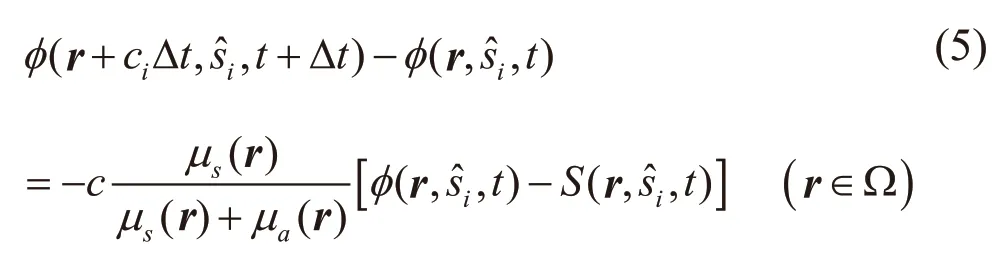
其中φ(r+ci△t,si,t+△t)表示在下一个时刻，在离散速度方向上的平均功率能量密度。S(r,被离散化为:用罗宾边界条件处理边界上的权值变化，最后通过ART重建计算结果。

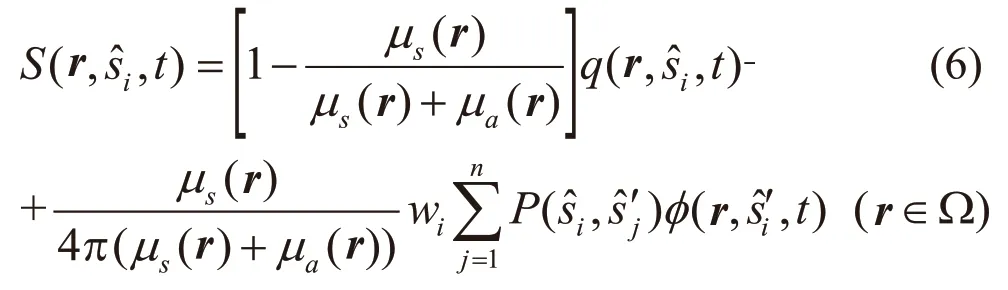
综上所述，本研究建立了基于LBM的FDOT的前向模型并介绍了重建方式。

2 结合GPU的格子玻尔兹曼前向模型

由于LBM节点的独立任务的内存需求相对较低，考虑LBM固有的并行性，这种方法非常适合在GPU上实现。通过使用GPU和CUDA通用并行计算架构对LBM进行编程，以加速基于格子玻尔兹曼前向模型的计算任务。本方法的框架如图1所示。框架分为两部分：CPU和GPU。与CPU相关的程序包括网格建立、坐标离散化、边界参数计算、CPU-GPU数据传输、代数重建和数据可视化。GPU相关程序主要由碰撞处理、迁移处理和边界处理组成。

其中，wi表示相位函数的离散权重因子。在LBM中，通常使用DmQn来描述粒子的空间维度和离散速度方向，其中m和n分别代表空间维度和离散方向。为了简化模型复杂度，在仿真和仿体实验中选择D3Q6模型，即三维六个离散速度方向模型，定义wi=1/6，i=1,2,3,4,5,6，并采用各向同性的介质。生物组织的光学参数（如吸收系数和散射系数）和组织边界被离散在均匀分布的立方网格上，从LBM的角度来看，光子被视作离散在网格中的粒子，而描述生物组织中光子传播的LBM主要可以分为碰撞和迁移过程，分别是：

图1 基于LBM的FDOT在GPU上并行化实现Fig.1 Parallel implementation of LBM-based FDOT on GPU

因此粒子在离散网格上不断地进行碰撞和迁移以模拟光子在生物组织中的传播过程。通过对网格上每个节点的6个相邻节点对应的分布函数进行计算，每次迭代后更新当前节点的分布函数值和平衡分布函数，即模拟光子在传播过程中当前位置的能量权值随时间的变化过程。本研究采

利用两级并行将所有LBM的节点值分配给每个线程。在第一级中，每个线程网格由几个线程块组成。当调用CUDA核函数时，线程块的线程在一个多处理器（MP）上同步执行。在第二级，每个线程块由多个线程组成，每个单独的LBM的节点值被分配给线程，每个线程将在流处理器（SP）上独立执行。在其实际操作中，核函数以线程网格的形式组织。为了避免数据竞争并确保同步，分别创建了三个主要的核函数并按顺序运行每个核函数。在编译程序之后，CUDA将计算任务映射到硬件从而以动态调度的方式执行线程，主要针对基于LBM的碰撞、迁移、边界处理过程进行并行加速计算。式（7）表明了碰撞过程只涉及当前位置节点的相关参数的计算，通过分别启动多个线程对单个节点的计算所需的参数读取，从而完成并行计算碰撞过程；式（8）表明了迁移过程只涉及当前位置节点的相应离散方向上的数据转移，通过启动两个不同的线程对单个节点的数据根据迁移方向覆盖至下一个节点，即可完成迁移过程；而对于边界处理过程，我们选择了掩模处理方法。对已经离散化的网格模型，完成边界定义，生成一个与生物组织网格模型大小一样的掩模矩阵，分别用0、1区分边界和非边界区域。当启动GPU线程时，仅对掩模标记为1的区域进行边界化处理。

CUDA的硬件层面分为主机（Host）端和设备（Device）端。基于LBM的FDOT的完整CUDA算法流程如下：

（1）确定合适DmQn的形式和离散权重；

（2）对三维生物组织模型进行网格化，包括吸收系数、散射系数等；

（3）对探测器采集的数据进行相同离散尺寸的网格化；

（4）将计算涉及的数据由Host端传输到Device端；

（5）对n个离散方向的粒子进行LBM计算：包括粒子的碰撞、迁移、边界处理、更新，直到模型达到稳定状态或者迭代次数上限的计算；

（6）当完成核函数的计算任务，Device端的计算结果传输回Host端；

（7）对计算结果进行ART重建；

（8）对重建结果进行可视化操作。

综上所述为结合GPU的并行化实现过程。

3 实验与结果

为了验证所提方法，我们选择8核、16 GB内存、64位、装有NVIDIA GTX660显卡的个人电脑进行实验。操作系统为Windows 7。本研究使用CUDA 6.5，OpenMP 4.0和Visual Studio 2012进行编译。

在单个GPU上进行实验测试，本研究不涉及GPU集群和消息传递接口（MPI）。实验由仿真实验和仿体实验两部分组成。为了简化模型，均匀介质圆柱体的吸收系数μa和散射系数μs分别选择0.3 cm-1和10 cm-1。前者旨在评估在相同编译环境下的加速度和准确性，在仿真实验中，分别实现了C++串行，GPU并行和OpenMP三种不同的编程方法，并具体分析了当LBM的网格尺寸分别为15×15×26，31×31×51，41×41×61，51×51×81，51×51×101，61×61×81时的性能指标；后者通过与传统扩散方程相比来验证所提方法的实用性。基于扩散方程方法通过有限元方法求解，有限元方法在Matlab中使用Gmsh[8]和Toast++[9]完成求解，其中Gmsh用于FEM的网格生成，Toast++用于FEM的求解。

3.1 仿真实验

实验采用一个里面嵌有两个圆柱体的大圆柱体模拟均匀介质下的光传播情况。采用半径为1.5 cm、高5 cm的大圆柱体模拟整个物理模型，采用两个半径为0.1 cm、高0.2 cm的小圆柱体分别模拟两个不同位置的荧光标记团，记为FT1和FT2。假设大圆柱体的底部圆心作为三维坐标系（x，y，z）的原点，布置不同位置的FT1和FT2以模拟不同情况，从而证明方法的稳定性。本研究实现了3种模拟情况，分别命名为Case1、Case2和Case3，如图2所示。FT1和FT2的具体坐标如表1所示。

在保证同C++的计算结果一致、精度误差极小的前提下，使用所提方法可以得到Case1至Case3的、离散尺度分别为15×15×26和61×61×81的重建结果，如图3所示，图3（a）代表离散尺度为15×15×26的重建结果；同理图3（b）代表离散尺度为61×61×81的重建结果。其中黑色粗体圆分别表示真实荧光团（圆柱体形状）所在位置。从图3可以发现，我们所提方法具有较好的准确性。网格模型离散尺度为61×61×81的图像重建质量远好于离散尺度为15×15×26的重建结果。

为了对所提方法的加速度进行评估，我们统计了C++、openMP、GPU三者方法的对于Case1至Case3的多次平均计算耗时情况，如表2所示。从表2中可以发现，当处理离散尺度为15×15×26的网格模型时，三者的耗时情况在同一个数量级；但当处理离散尺度不断增大时，基于GPU的并行化的优势逐渐明显；这是由于C++串行算法无法利用好资源，受到算法流程的限制，只能做等待，计算资源的利用率很低；OpenMP处理小尺寸的网格模型时，系统内存资源丰富，可以有充足的空间进行数据复制和线程切换，但是当处理大尺寸的网格模型时，在线程之间切换需要额外的内存空间以释放资源，从而导致处理速度变慢；而GPU与LBM的契合性较高，在处理较大离散尺寸的网格模型时拥有并行性，提升了计算效率。

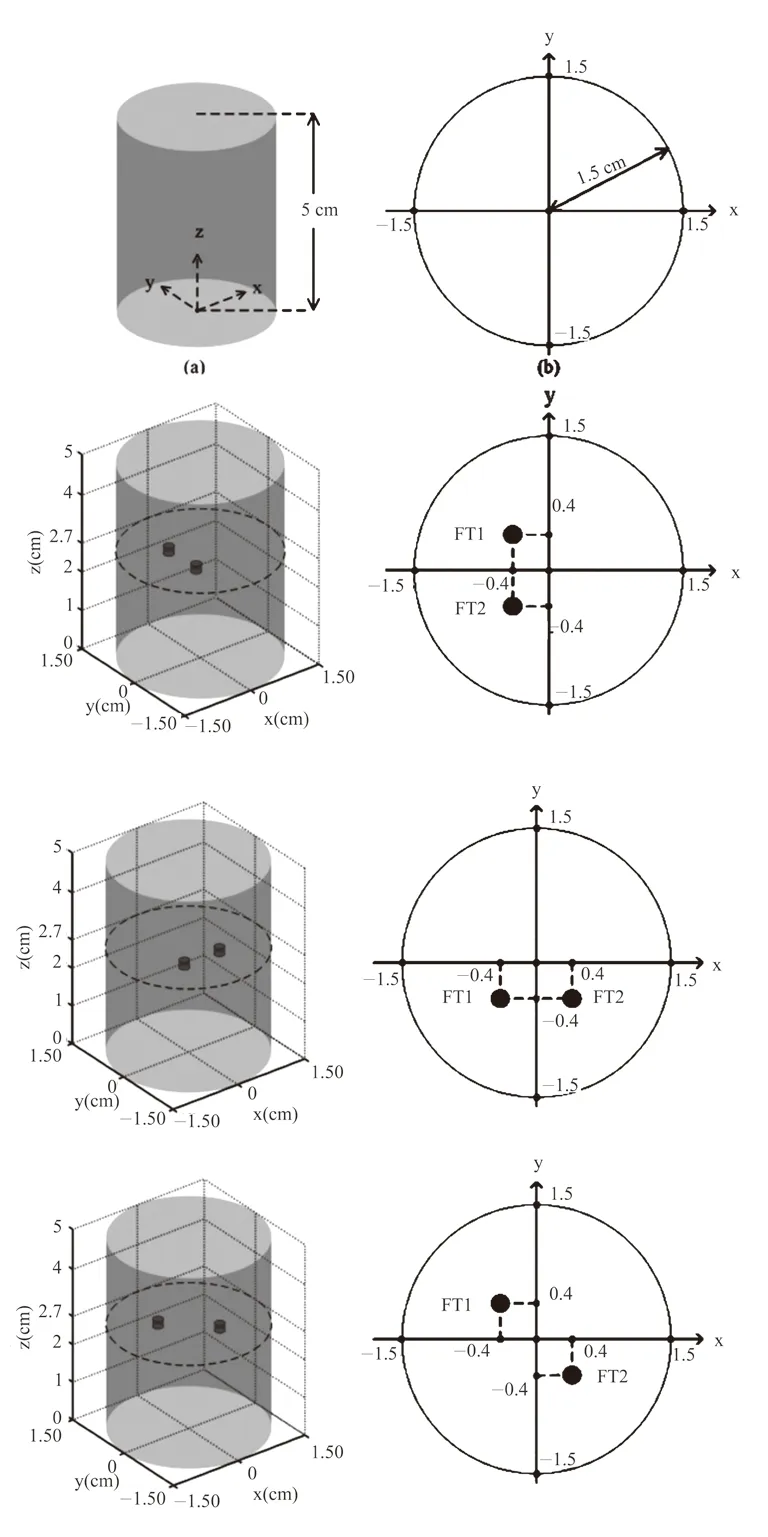
图2 数值仿真实验的Case1至Case3的实验设计示意图Fig.2 Diagram of experimental design of Case1 to Case3 in numerical simulation experiments

表1 三种数值仿真实验的荧光团具体坐标Tab.1 Specific coordinates of fluorophores in three numerical phantom experiments

图3 基于不同离散尺寸的网格模型的FDOT重建结果Fig.3 FDOT reconstruction results based on mesh models with different discrete sizes

表2 基于C++、OpenMP、GPU的三种不同编程方式的计算耗时统计Tab.2 Computing time-consuming statistics based on C++,OpenMP and GPU

3.2 仿体实验

采用FDOT/XCT混合成像系统，将待成像物体放置在360o旋转台上缓慢旋转，通过CCD相机测量从仿体表面溢出的光子的辐射强度，细节见GUO[10]的文章。本研究将直径为0.4 cm的荧光团管状物嵌入高度为4.4 cm、半径为1.5 cm的圆柱体中作为仿体模型。

通过对比基于DE方法的求解结果从而验证我们所提方法的实用性。基于所提方法的LBM网格节点和基于DE方法的网格元素个数分别采用49 011离散节点和50 469个节点从而保证二者方法的节点个数相近以公平对比。本研究可视化了计算尺寸为31×31×51的计算结果，如图4所示，（a）为真实仿体的示意图；（b）为基于LBM的重建结果；（c）为基于DE方法的重建结果。LBM的重建结果有明显的伪影，但中间荧光团的形状几乎相同，与基于DE方法的计算结果保持一致。

图4 仿体实验的重建结果对比Fig.4 Comparison of reconstruction results of physical phantom experiments

表3为基于LBM方法和基于DE方法的耗时对比。当计算尺寸为15×15×26时，本研究的方法计算速度比基于DE的方法快25倍；当计算尺寸为31×31×51时，本研究的方法计算速度比基于DE的方法快118倍；当离散尺度更大时，受到内存资源的限制，基于DE的方法无法求解，而本研究的方法仍然可以求解。

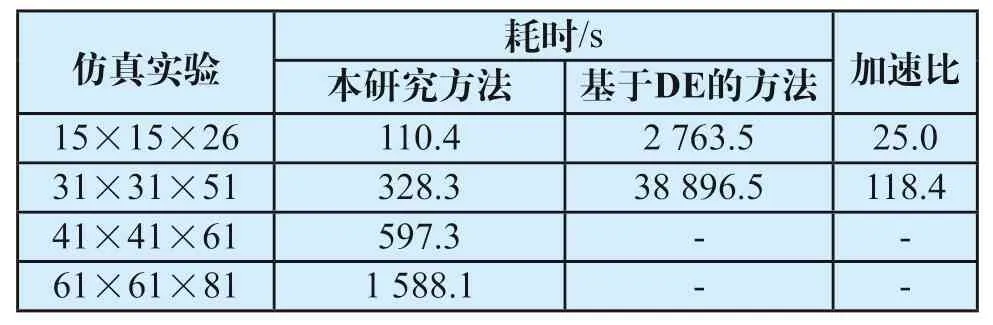
表3 基于LBM方法和基于DE方法的计算耗时Tab.3 Time consumption obtained by the DE and LBM method

4 结论

综上所述，本研究验证了所提方法的准确性和加速性。结果表明，本方法可以在保证准确性的前提下，快速求解，有助于LBM的发展和FDOT的快速成像。但是本研究提出的方法仍然存在一些待改进的地方：基于LBM的FDOT的光传输模型没有解释如何对离散时间和离散空间做耦合；D3Q6作为实现模型，过于简化，带来了伪影现象；生物模型做了较多的简化，在实际应用中仍然需要复杂化；基于GPU的结合方法目前仍然无法满足实时的动态FDOT的技术需求。在今后的工作中，将重点研究非均匀介质、不规则形状和GPU集群方向。