脑电信号分析方法及其应用

周晶晶，叶继伦,，张旭,，李晨洋，檀雪

1 深圳大学 医学部 生物医学工程系，深圳市，518060

2 深圳市生物医学工程重点实验室，深圳市，518060

3 广东省生物医学信号检测与超声成像重点实验室、深圳市生物医学重点实验室，深圳市，518060

0 引言

EEG信号是研究大脑科学活动的重要手段之一，可使用电生理指标来记录反映大脑头皮神经元兴奋性和抑制性突触后电位的潜在活动[1]。用ECG来分析大脑的活动，具有无创、实时、连续、时间分辨率高以及认知意识相关性强等特性，是目前临床医学研究中不可或缺的手段，也是实验室重点研究的生理信号。利用脑电信号反映麻醉深度能够指导临床手术，研究脑电信号在疲劳状态下的性质，能够判断司机疲劳驾驶程度等，因此研究脑电信号具有很重要的作用。

EEG信号的频率分布主要集中在 0.5～30 Hz，EEG信号幅值大多在5～200 μV之间[2-3]，是典型的极其微弱的非平稳随机信号。EEG信号的临床应用通常根据频率段将EEG分成几个不同的信号段，依次称为δ波（1～3 Hz）、θ波（4～7 Hz）、α波（8～13 Hz）、β波（14～30 Hz）[4]。δ波在睡眠、缺氧、疲劳、麻醉等状态下会出现，θ波会出现在疲惫时，α波出现在清醒和闭上眼睛时，β波出现在精神波动和情绪紧张或兴奋时。不同大脑状态，各频率段所占能量不同，为研究脑电活动提供了基础。

本研究主要从三个方面对脑电信号进行处理，分别从时域、频域和功率谱估计等方面对脑电信号做特征分析，研究脑电信号特征变化，为处理脑电信号提供参考价值。

1 功率谱分析

功率谱分析方法是一种非常重要的频谱分析方法，功率谱分析主要探讨信号能量随频率的变化情况，即在频域的信号能量分布状况。功率谱估计主要分为两类：经典功率谱（如直接法、自相关法）和参数模型（AR模型）功率谱[5]。经典功率谱估计方法的性能较差，分辨率较低。性能差的主要原因是不能实现功率谱密度原始定义中平均值和极限的运算，分辨率低的原因是周期图法假设数据窗外的数据全是零，对于自相关方法是假设在延迟窗以外的自相关函数全是零。参数模型法是现代谱估计的主要内容，具有较高的频率分辨率和性能。

1.1 经典功率谱

（1）直接法

直接法又叫做周期图法，它将随机信号x(n)的N点观察数据xN(n)视为一个能量有限信号，直接对xN(n)进行傅里叶变换得xN(ejw)。然后，取其幅值大小的平方，并除以N，作为对x(n)真实的功率谱P(ejw)的估计。由周期图法估计出来的功率谱PPER(ejw)表示:

直接法截短无限长平稳信号，相当于对信号添加矩形窗，使窗函数和功率谱卷积。该卷积导致频谱泄露，并且当数据长度N太大时，谱曲线波动加剧，并且如果N太小，谱的分辨率会较差。

（2）Welch法

Welch法[6]是对周期图方法的改进，利用平均法改进其方差特性，得到加权交叠平均法，即Welch平均周期图法。它的指导思想是将xN(n)数据长度N分成L段，并分别计算每一段的功率谱，然后对其平均，在分割时允许每个数据存在部分重叠。每段的窗口可以是矩形窗口，可以是汉明窗也可以是汉宁窗。根据Welch法，每段的功率谱记为即

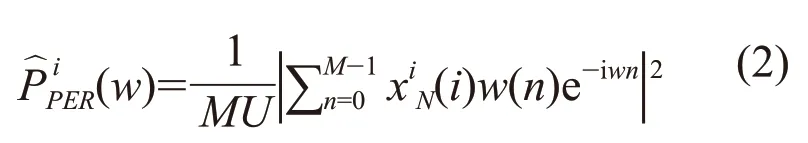
式中M为每段数据，也是窗长度，是归一化因子，它用于保证得到的频谱是渐进式无偏估计。因此，Welch平均法得到的平均功率谱为：

1.2 参数模型功率谱

参数谱估计法假定所研究的信号是由输入激励线性系统的输出模型产生，然后对模型的参数进行估计，再从中得到谱特性。当假设模型非常接近实际情况时，参数模型很容易响应谱中的峰值，能得到更准确的谱估计。

无论x(n)是确定性信号还是随机信号，参数模型的线性系统都有如下输入输出关系：

u(n)是方差为σ2的白噪声序列，对两边各取Z变换，并假定b0=1，可以得到传递函数：

输出功率谱密度为：

设b1,b2,...,bq全为0，那么：

我们把（8）（9）（10）三式称作自回归模型，即AR模型[7]，它是一个全极点模型。“自回归”的含义是：模型的输出是当前输入和过去p个输出的加权和。由于AR模型是有理分式，因此估计出的谱比经典法的谱光滑无毛刺并且具有高分辨率的特征。

1.3 功率谱估计分析

该研究采用直接法和Welch法两种经典模型的功率谱估计和AR参数模型的功率谱估计对脑电信号进行功率谱分析，图1是原始时域EEG信号及其幅值谱，图2是三种功率谱分析图，从图2中可以明显看出，直接法效果较差，Welch法和AR模型估计的功率谱效果较好，从功率谱分布图可以得出该信号能量主要集中在δ段，可能是处于麻醉深度或疲劳状态，对临床上判断麻醉深度具有参考作用。

图1 时域和频域图Fig.1 Time domain and frequency domain diagram

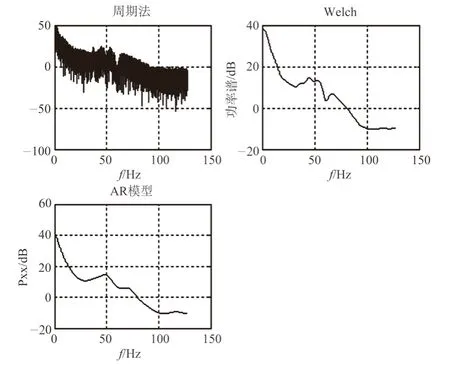
图2 功率谱估计图Fig.2 Power spectrum estimation diagram

2 时频分析

2.1 短时傅里叶变换

由于EEG是时变非平稳信号，因此信号的频率随时间改变而改变，传统的傅里叶变换缺少时域定位的功能，为了解EEG信号时频信息，我们采用短时傅里叶变换对脑电信号进行处理。

给定一信号x(t)∈L2(R)：

式中：

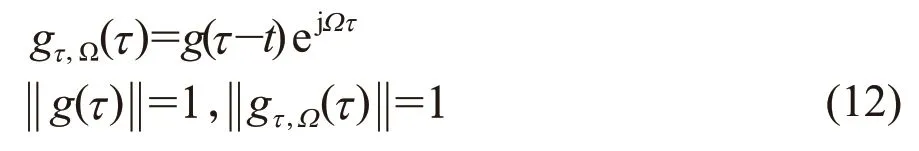
短时傅里叶变换的思想是使用窗函数g(τ)来截取x(τ)，通过对截断的局部信号进行傅里叶变换，可以获得不同时间t信号的傅里叶变换。然后不断移动时间t，即连续移动窗函数g(τ)的中心位置，即可连续得到不同t时刻的傅里叶变换。这些移动时间t获得的傅里叶变换的组合就称为短时傅里叶变换[8]。

如图3所示，是Matlab下处理脑电信号的短时傅里叶变换图。从图中可看出信号频率随时间变换的关系，然而短时傅里叶变换也具有局限性，不能同时优化频率与时间分辨率，且时频窗的面积不能小于1/2。

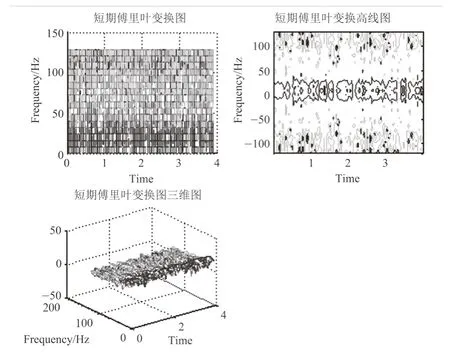
图3 短时傅里叶变换Fig.3 Short-time Fourier transform

2.2 Wigner分布

Wigner分布又称Wigner-Ville分布，简称为WVD。令信号x(t),y(t)的傅里叶变换分别是X(jΩ),Y(jΩ),那么x(t),y(t)的联合Wigner分布定义为：

信号x(t)的自Wigner分布定义为：

Wigner分布反映信号能量随时间和频率分布的关系，具有一系列良好的时频性质[9]，如对称、时移、组合和复共扼等，不会损失信号的幅值与相位信息，对瞬时频率和群延时有清晰的概念，所以在时频分析中具有很重要的地位。但由于Wigner分布是双线性变换的形式，因此两个信号和的分布将存在交叉项干扰[10]，它会影响信号时频行为的识别，这也是二次时频分布的必然结果。

图4是Matlab下EEG的Wigner三维分布图，可以看出它的时频分辨率优于短时傅里叶变换。

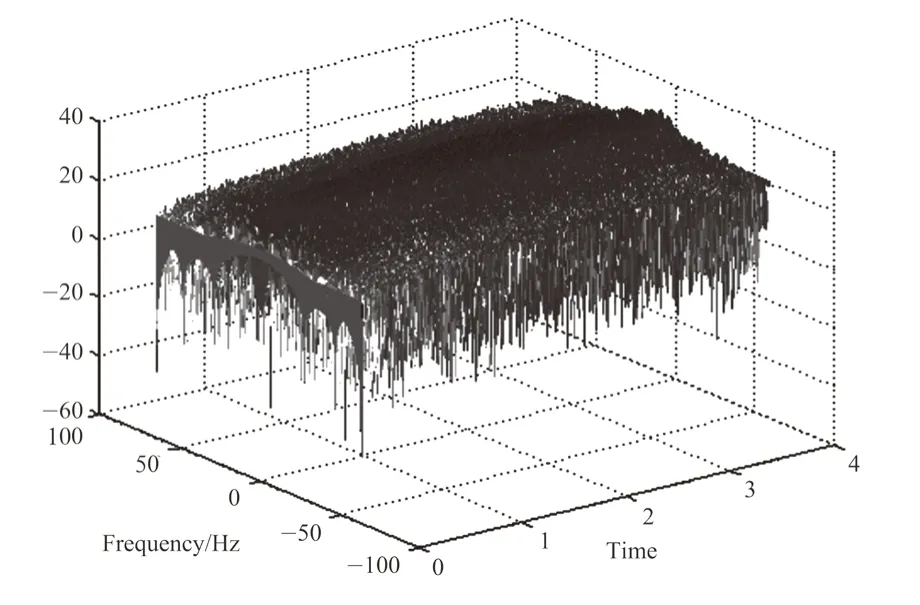
图4 脑电信号wigner分布三维图Fig.4 Wigner distribution of EEG

2.3 小波变换[11-12]

小波变换可以分析局部信号的时间和频率[13]，通过平移和伸缩对信号（函数）逐步进行多尺度细化，最终可以使分析的信号在高频处具有高时间分辨率，低频处具有高频率分辨率，因此小波变换能专注于信号的任意细节，解决了傅里叶变换的难题，并且可以适应不同频率范围内不同分辨率的信号分析的基本要求。

小波变换的定义是给定基本函数ψ(t)：

式中：a,b均为常数，且a＞0。ψa,b(t)是对基本函数做ψ(t)平移和伸缩之后得到的函数。如果a,b连续变化，可得ψa,b(t)函数的集合，给定平方可积的信号x(t)，即x(t)∈L2(R)，则x(t)的小波变换定义为：

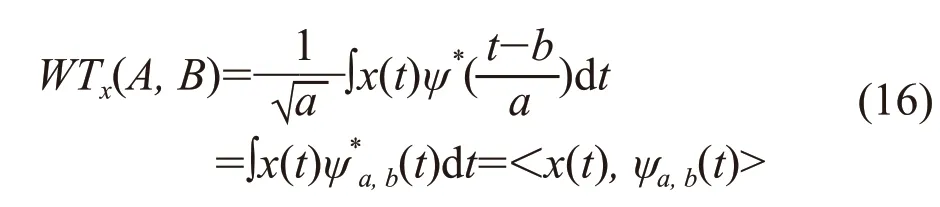
式中a,b和t均是连续变量。所以该式也称为连续小波变换（CWT），信号x(t)的小波变换是a和b的函数，b是时移，a是尺度因子。ψ(t)又叫基本小波，或者母小波，ψa, b(t)是母小波经平移和伸缩后产生的函数集合，称为小波基函数。因此WT又可解释为信号x(t)和一组小波基的内积。

小波变换能够在时域和频域中描述信号局部的特征。小波变换可以将信号的频谱分解成不同的频率段，然后把信号的能量集中到某些频带的几个系数上，通过把其他频带上分解的系数置零或是给小一点的权重，能够较好抑制噪声[14]。该研究使用db4小波对EEG信号去噪，可以取得良好的效果。如图5所示，小波去噪后的信号比原始信号更平滑，边界更清晰，而且可以去掉很多毛刺。

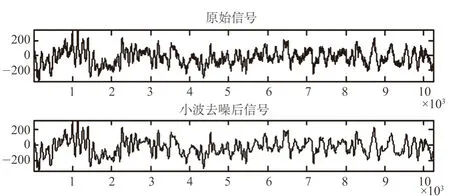
图5 脑电信号小波去噪Fig.5 Wavelet denoising of EEG signal

3 双谱分析[15]

因为脑电信号中存在大量非线性耦合现象，所以研究脑电信号的非高斯特征、非线性特征也很重要[16]。虽然功率谱分析可以反映信号的二阶信息，但是会丢失包括相位信息在内的高阶信息[17]，因此研究脑电信号的非线性特征最常用的方法是对信号进行高阶累计量的分析。

双谱密度函数定义为：

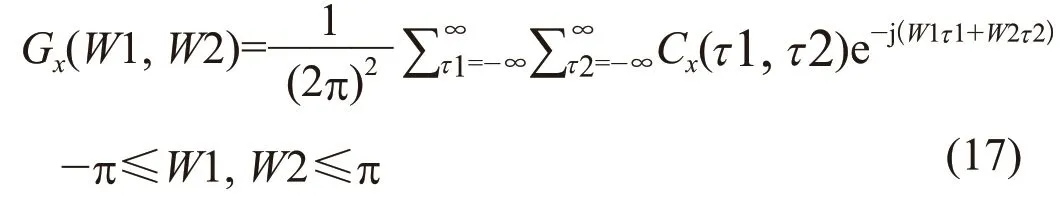
双谱分析具有很多性质，如双周期、对称性、复函数，可通过振幅与相位来表示等。

根据观测数据长度的限制，实际信号的双谱估计通常分为两大类[18]，第一类是参数模型估计法，第二类为非参数估计法，其中非参数估计法包括直接估计法和间接估计法。直接估计法使用的是离散傅里叶变化的三阶周期法，间接估计法通过对三阶累积量加窗并进行二维傅里叶变换得到。该研究采用双谱直接估计法。

图6为在Matlab环境下对脑电信号做双谱估计的三维图，双谱图中包含信号的能量、幅度信息、信号的相位，可以作为检测EEG的非高斯和非线性特性的重要工具[19]。双谱估计三维图不能准确描述固定频率与其他频率的耦合，而二维切片可以清楚地得到该信号和其他频率的非线性耦合。如图7所示，是该EEG双谱估计三维图的平面切图，能够反映双谱分析的一部分信息，提取双谱特征值将有益于分类器基于特征值的分类[20]。

图6 脑电信号双谱估计三维图Fig.6 Three-dimensional estimation of EEG signal bispectrum

图7 双谱估计切片图Fig.7 Bispectral estimation section diagram

4 应用

该研究建立了初步的脑电测量系统，根据以上的信号处理介绍，选择了相关的方法进行噪声及特征参数的分析，其中功率谱计算主要用于分析脑电信号各频段的能量所占的比例，对于麻醉和疲劳等状态下EEG不同频段分期具有良好的参考价值，可用于麻醉深度的检测和疲劳程度的划分，对于指导脑电信号的应用具有重要的意义。时频分析多用于光滑原始信号，获得较高质量的信号，从而进行特征提取等。双谱分析可显示传统脑电图无法显示的信息，以及通过脑电信号三阶能量在双频域中各频段的分布，研究不同脑功能状态下的脑电信号，为我们了解大脑功能提供了一种新的分析方法。