从一道武汉中考题入手探讨圆的折叠

江苏省常州市武进区湖塘实验中学(213161) 顾超德

以折叠为背景的几何问题在近几年的中考中属于热点问题,题型灵活多样,体现的是轴对称变换的思想．学生往往对直线型图形的折叠问题比较熟悉,而遇到圆的折叠,学生往往束手无策,这对学生图形识别、空间想象、综合解题等方面的能力提出了更高的要求．解决这类问题时涉及的知识点多、综合性强,是培养学生实践操作能力和数学核心素养的一条有效途径．

1 试题呈现

(2018·武汉中考数学试题)如图1,在⊙O中,点C在优弧上,将弧沿BC折叠后刚好经过AB的中点D．若⊙O的半径为则BC的长是( )．

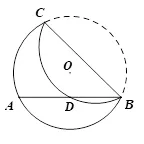
图1

A.2B.3C.D.

本题作为选择压轴题,将垂径定理,圆周角定理,轴对称,三线合一,勾股定理等知识融和一体,具有很强的综合性．首先,圆中问题常见的切入口是半弦,弦心距、半径构成的直角三角形,利用勾股定理可以求解相关线段．对于圆心的处理,我们常常是构造直径,得到对应的圆周角是直角．

2 解法呈现与分析

如图2,连接OD,OA,AC,DC,作CE ⊥AB于E．因为D为AB的中点,所以OD ⊥ AB,所以2 ．在__Rt__ΔAOD中,OD=．因为将弧沿BC折叠后刚好经过AB的中点D,所以弧和弧所在的圆为等圆．因为所对的圆周角是∠ABC,所对的圆周角是∠DBC,所以,所以AC=DC,所以AE=DE=1．

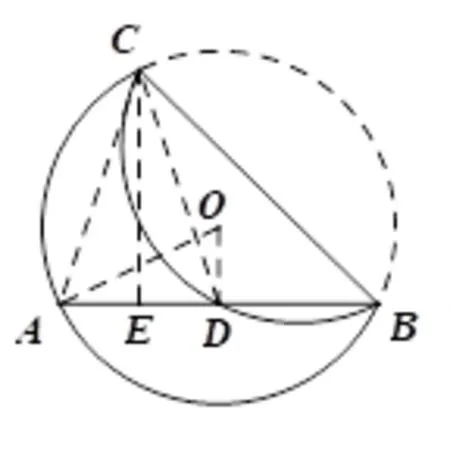
图2

图3

思路2如图4,连接AO并延长,交⊙O于点G,则∠ABG=90°,OD是ΔABG的中位线．所以BG=2OD=2,所以BG=BD,所以．又因为所以所以∠DBC=∠GBC=45°．所以,在等腰RtΔCEB中

图4

3 模型归纳与总结

结论如图5,在⊙O中,将弧沿BC折叠,交AB于点D,则CA=CD,即ΔACD是等腰三角形．

证明如图6,在弧上作出点D的对应点D′,连接BD′和CD′,则有DD′⊥BC,∠ABC=∠D′BC．所以,所以CA=CD,即ΔACD是等腰三角形．证毕．

图5

图6

推论1如图7,当折叠后弧经过圆心O时,ΔACD是等边三角形．

证明如图8,在弧上作出点O的对应点O′,连接CO,CO′,BO,BO′和OO′,OO′交BC于点E．则有OO′⊥BC,CO=CO′,BO=BO′．因为CO=BO,所以CO=CO′=BO=BO′,所以四边形COBO′是菱形．因为所以∠COE=60°,∠COB=2∠COE=120°,所以因为是等腰三角形,ΔACD是等边三角形．证毕．

图7

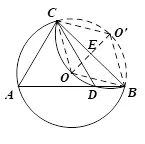
图8

推论2如图9,延长CD交⊙O于点P,ΔBDP是等腰三角形．

证明在ΔACD和ΔBDP中,因为∠ACD=∠DBP,∠CDA=∠BDP,所以∠CAD=∠BPD.又因为∠CAD=∠CDA,所以∠BPD=∠CDA=∠BDP,所以BD=BP,即ΔBDP是等腰三角形．证毕．

图9

Arzberg在 1920 年末与Hermann Gretsch大师合作推出新系列“1382”而名垂千史，该系列产品从1931 年便炙手可热，有一位评论家给“1382”极高的评价，称之“实用、朴实，简洁的风格比肤浅的时尚更具经典意义”。

有了以上结论,学生在处理圆中折叠问题时,可以综合利用圆,轴对称,直角三角形等知识,有效地解决相关问题．

4 实例应用

例1:如图10,在⊙O中,将弧沿弦AB翻折,交半径AO的延长线于点D,延长BD交⊙O于点C,AC切圆弧所在的圆于点A,则tan ∠C的值是( )．

A.B.C.2+D.1+

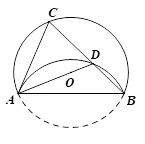
图10

图11

解答如图11,延长AC交⊙O于点E,连接BE．作点O关于AB的对称点O′,连接AO′．

由上述已知结论可知,AC=AD,BD=BE．由对称性易证点O′是所在圆的圆心,∠OAB=∠O′AB．因为AC切圆弧所在的圆于点A,所以AC ⊥AO′．过点A作AF ⊥CD于F,因为AC=AD,所以∠CAF=∠DAF,所以．所以在RtΔABF中,∠ABC=45°．因为AE是⊙O的直径,所以∠ABE=90°,所以∠DBE=45°．所以．到此,题中的问题就转化为在等腰ΔACD中,AC=AD,∠CAD=45°,求底角∠C的正切,具体的过程读者自行完成,答案是

评析本题的关键步骤是要做出点O的对称点O′,利用相切得到∠CAO′=90°,从而得到∠ABC=∠DBE=45°．在最后求∠C的正切时,可以过点D作AC的垂线．

例2:(多次折叠) 如图12,AB为半圆O的直径,将劣弧沿BC翻折,与直径AB交于点D,再将劣弧沿BD翻折,与BC交于点E．若点E恰好是BC的中点,则tan ∠ABC＝( )．

图12

图13

解答如图13,连接AC,CD,DE,OE,作DN ⊥BC于点N,作CG ⊥AB于点G．题中经历了两次圆弧的翻折,由已知结论可知:AC=CD=DE,所以CH=EH,AG=DG．因为点E是BC的中点,所以OE ⊥BC．因为AB为直径,则AC ⊥BC,所以AC//DN//OE,所以所以．设AG=m,则AB=8m,BG=7m．因为ΔACG∽△CBG,所以CG2=AG·BG=m·7m=7m2,所以所以

评析本题应用了两次圆中折叠的性质,综合应用了“三线合一”、中位线、圆周角定理的推论,来构造了一组平行,得到了线段之间的比例．再利用相似的性质(射影定理)来求得线段的比值,总的来说,本题的难度较大．

例3(2016·天门中考数学试题)如图14,⊙O的半径是5,CD是⊙O的直径．点E为圆上一点,∠ECD=15°,将沿弦CE翻折,交CD于点F,求图中阴影部分的面积．

图14

图15

解答(方法一) 如图15,连接DE,EF,作点O关于EC的对称点O′,连接FO′,CO′,．根据已知结论,知ED=EF．由CD为⊙O的直径,得∠CED=90°,所以∠EFD=∠D=90°-∠ECD=75°,∠FEC=∠EFD-∠ECD=75°-15°=60°,所以∠FO′C=120°．所以

(方法二)如图15,由对称性可知,∠ECO′=∠ECD=15°,所以∠FCO′=∠CFO′=60°,所以∠FO′C=120°．下同方法一．

(方法三)如图16,在弧上作出点F的对应点M,将阴影部分沿CE翻折,点F的对应点为M．由对称性可知,∠DCM=2∠ECD=30°,

连接OM,则 ∠MOD=60°,∠MOC=120°,所 以

图16

折叠问题的本质是轴对称．在解决折叠问题时要紧紧抓住对称的特征:折叠前后的图形全等,对应部分相等,以及对应点的连线段被对称轴垂直平分．对于圆中的折叠问题,除用好轴对称的性质,还要注意圆的特殊性,找准其解题关键突破口,作出折叠后的弧所在圆的圆心．突破难点后,问题便转化成我们熟悉的显性圆的常规问题,然后,综合利用圆的各种性质、相关定理、公式,使问题得以解决．