房地产投资对GDP增速的实时预测效果分析——基于混频数据抽样模型

吴俊仪 程建华

（安徽大学经济学院 安徽合肥 230601）

房地产投资是我国固定投资中一个重要的组成部分，长期以来我国房地产投资以较高的速度稳定增长，对我国经济稳增长这一长期策略发挥重要作用。在经济预测领域，鲜有学者尝试利用月度指标房地产投资对季度指标GDP增速进行实时预测及其预测效果研究。鉴于此，本文采用向前h步预测的自回归混频数据抽样模型与传统的同频数据模型，分别对我国的房地产投资与固定投资、消费以及出口实时预测GDP增速的效果进行实证分析，将结果进行分析比较，期望应用房地产投资增长率对经济增长率的实时预测，对现有经济增长率预测的准确性和及时性做出改善。

GDP增速作为一种衡量国家或地区经济整体水平的综合性指标，其未来趋势变化始终被经济学家及政策制定者们所关注。由于GDP数据发布频率较低，时滞较长，很多学者希望通过更高频率的月度或日度指标更快更有效地预测GDP的走势。为此Ghysels等（2004）率先提出了混频数据抽样模型（MIDAS），他们巧妙地运用权重函数将高频解释变量嵌入回归模型中，对低频被解释变量进行预测。[1]这种方法一经提出，受到了国内外学者们的广泛关注，很多学者将该模型应用到宏观经济领域，且研究结果得出较为一致的结论：混频数据抽样模型不仅能充分利用高频数据里包含的信息，还可以提高预测的精准度。比如Celements和Galvao等（2009）运用MIDAS 模型对美国的经济增长进行实时预测，结果发现先行指标都具有显著的预测能力，且在预测季度增长率时，使用高频的月度数据预测效果更好[2]。Ibarra R 等（2017）则使用了更加高频的日度数据，他们采用MIDAS模型，利用财政日度数据对墨西哥GDP增长速度进行预测，发现相对于利用季度数据或日均数据并采用传统模型的预测而言，包含日度财政数据的MIDAS 模型预测效果明显改善[3]。我国学者李正辉、郑玉航（2015）还将混频数据抽样模型应用到了经济周期的区制监测中，他们构建了马尔科夫区制转换混频数据模型，结果发现该模型在监测经济周期波动时，相较于同频数据基准模型而言，预测精度明显提高，捕捉经济周期波动的及时性明显改善。[4]

而作为拉动我国经济持续增长主要因素之一的房地产投资在我国现有经济增长实时预测中并不多见，相对于固定资产总投资，房地产投资市场的敏感性更强，应用市场敏感性更强的经济指标用于经济增长预测可提高经济预测的实时性，其也更符合实时预测本身意义。

一、模型构建

（一）单变量MIDAS(m,k)模型。单变量MIDAS 模型源于分布滞后模型的思想，用高频数据来解释，预测低频数据的一种模型。单变量MIDAS（m,k）模型如下：

对于权重函数设定，主要有Almon 函数、expAlmon 函数、beta 函数、step 函数，非限制型 MIDAS（U-MIDAS）的形式。

（二）包含自回归项的MIDAS(m,k)-AR(p)模型。为进一步提高模型精度，考虑到宏观变量可能存在自相关性，本文在单变量模型基础上引入带有滞后阶数被解释变量的自回归项，包含自回归项的MIDAS(m,K)-AR(p)模型如下：

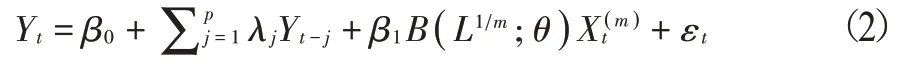
（三）向前h 步预测的MIDAS(m,k,h)-AR(p)模型。因为数据公布具有时滞性，为达到实时预测的目的，本文引入h步向前预测的MIDAS(m,k,h)-AR(p)模型，该模型的形式为：

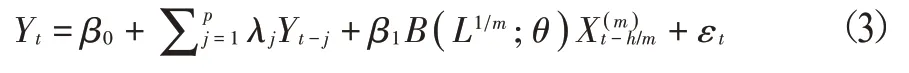
当该季度的第一个月度数据发布时，则令h=2，代表向前预测两期，即利用该月数据对季末的季度数据进行预测；同理，当该季度第二个月的数据公布后，令h=1，代表向前预测一期，即添加了第二月的数据再次对季末的季度数据进行预测。

（四）基准模型及预测误差衡量标准。另外，为突出混频模型优势，本文采用同期加总方法，运用同频数据分布滞后回归模型作为本文研究的基准预测模型。基准模型可写为如下形式：

其中，p=K/m。Xt-i指的是解释变量滞后i期。

为比较模型的预测效果，本文使用预测的均方根误差（即RMSE）来衡量

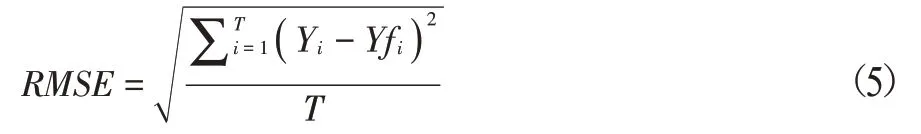
其中，i为对Yt预测的期数，取值范围是[1,T];T为最高预测期数；Yi是第i时期的真实值，Yfi是第i时期的预测值。

二、变量选取、说明及平稳性检验

本文使用季度GDP同比实际增长率Yt及月度社会消费品零售总额同比变化率月度出口总额同比变化率月度固定资产投资完成额同比变化率月度房地产开发投资同比变化率构建MIDAS模型（本文将2008年第一季度至2016年第四季度的数据作为估计样本，2017年第一季度至2018 年第四季度的数据作为预测样本）。数据均来源于中经网统计数据库。

其中，月度社会消费品零售总额的变化表示消费变化，若其上升，说明国内消费支出增加，表示我国经济状态呈向好趋势。出口反映了我国经济对外开放的程度，作为拉动我国经济发展的三驾马车之一，对我国经济增长的作用不容忽视。固定资产投资作为投资中最重要的部分，反映全社会投资的规模，是政策制定者判断经济走势、制定政策计划的重要依据。房地产投资不但是反映我国房地产市场变化的重要指标，还能凭借其极强的市场敏感度及时反映我国经济趋势的变化，近年来房地产对我国经济持续稳定增长起着举足轻重的作用，是促进我国经济发展的重要因素之一。

在构建时间序列回归模型时，若序列非平稳，则可能造成“伪回归”。故在进行实证分析之前本文对季度GDP增长率及四个月度解释变量进行ADF检验，其P值均小于0.01，故上述变量均为平稳时间序列。故后文的MIDAS模型及基准模型都可直接使用这些原始数据进行预测和分析。

三、实证研究

（一）基于MIDAS模型预测结果分析。首先，分别利用五种不同权重函数的单变量MIDAS(m,k)模型，即模型（1）进行预测，给定K值分别为6、9、12、15、18（Clements和Galvao（2009）认为对于季度数据GDP 而言，月度指标的滞后阶数最好使用3的倍数，以便与同频的基准函数比较，在实证研究中，最长滞后阶数可选至2年）。利用模型（1）预测2017第一季度至2018第四季度共8个季度的GDP，为减少不必要的篇幅，本文仅列出基于ALMON 权重函数的RMSE，如表1所示。

表1 四种变量基于almon权重函数的RMSE

为简化后面的分析过程，本文在保证系数及模型的统计量显著的基础上，选择一种权重函数进行后面的计算。综合比较后选择Almon权重函数，理由如下：预测效果适中；添加因变量的滞后项后，参数仍然显著。房地产投资采用Almon权重函数时最小RMSE 值为0.615046，对应的模型为MIDAS(3,15)，它的估计结果如表2所示。

表2 房地产投资的MIDAS(3,15)模型估计结果

从表2可知，MIDAS(3,15)模型所有参数检验在5%水平上显著，模型的拟合程度较高（R2为0.841700），模型对数据的整体拟合程度较好，但仍有上升空间（表2以及后文表格中括号里数值均为t值）。对于宏观经济变量来说，在模型中引入自回归项往往会提高模型的预测精度。本文考虑自回归项0至4阶的变化，根据每种模型最小AIC信息值所对应的滞后阶数来选择自回归项的滞后阶数p，除消费的MIDAS(3，15)模型最小AIC信息值对应的滞后阶数为0外，其他模型最小AIC信息值对应的滞后阶数全部不为0。就此而言，可初步说明在模型（1）中嵌入自回归项的设定更为合理。考虑到文章篇幅，不再将全部模型参数估计结果列出。为方便与前文的房地产投资的MIDAS(3,15)模型对比，仅列出MIDAS(3,15)-AR(2)估计结果，如表3所示。

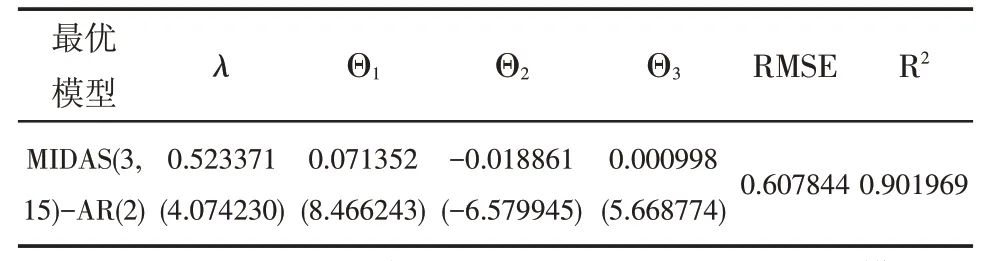
表3 房地产投资的MIDAS(3,15)-AR(2)模型估计结果

从表3 可知，房地产投资的MIDAS(3,15)-AR(2)模型的所有参数在5%的显著水平上显著。对比表2房地产投资的MIDAS(3,15)模型的估计结果可知，加入因变量自回归项后的模型在保持参数显著性的同时拟合优度R2明显改善，由0.841700 提升为0.901969。预测误差也稍有减小，由0.615046减少为0.607844。

上述模型仅实现了高频与低频数据的模型建立，实际应用中要涉及到对样本外的数据进行预测。为此，本文引入MIDAS(m,k,h)-AR(p)模型，即模型（3），在加入自回归项后向前h步预测，将实时更新的数据嵌入模型，实时修正预测结果。其中，h的取值范围为1至12，本文侧重数据短期内的预测效果，故在此仅展现向前1 期至向前6 期（即最多向前半年）的预测效果，如表4所示。

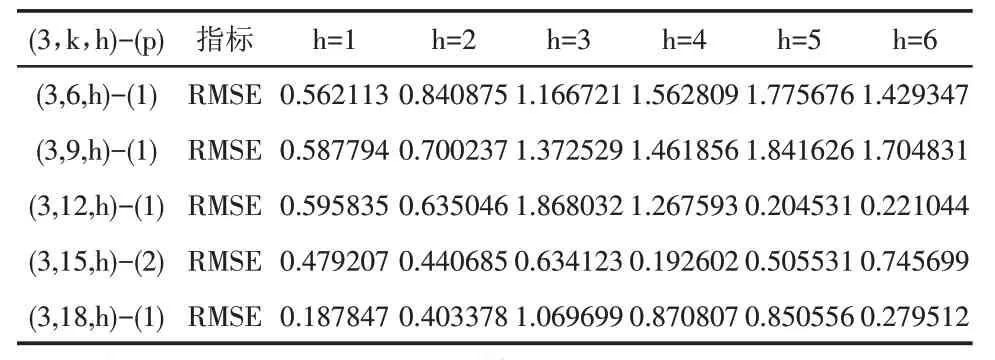
表4 房地产投资完成变化率的向前h步预测效果

本文根据RMSE 值判断模型预测效果，由表4 可知，当高频变量的滞后阶数为6和9时，若向前预测步数在5步以内，随着h的增加，房地产投资的预测误差增大，h取1时房地产投资的预测误差最小，分别是0.562113和0.587794。这种情况下，房地产投资更适合于短期预测。当高频变量的滞后阶数为12、15、18 时则不尽然，房地产投资的预测误差与向前预测步数h的正相关关系仅在h小于等于3时成立。而不论滞后阶数取何值，h取1时预测效果总是占优的，从表4可知，向前1 步预测时最大的RMSE 也仅为0.595835，说明MIDAS向前1步预测的方法在实时预测中具有稳健性。观察表4 知最小RMSE 值0.187847 对应的模型是MIDAS(3，18，1)-AR(1)，该模型是房地产投资实时预测GDP增速的最优模型。表5展示了房地产投资的MIDAS(3,8,1)-AR(1)模型的估计结果，该模型系数均在5%水平上显著，拟合优度为0.913745，说明该模型对数据拟合程度尚优。

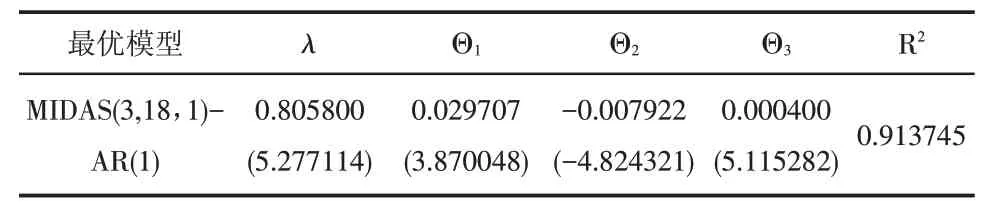
表5 房地产投资的MIDAS(3,18,1)-AR(1)估计结果

接下来本文将房地产投资向前1步预测GDP增长率的结果与其他三种变量向前一步预测的结果进行比较，表6展示了其预测误差RMSE值。

表6 四种指标向前1步预测GDP增长率的RMSE

从表6 可以看到，在向前1 步预测时，房地产投资的MIDAS(3，18，1)-AR(1)模型在四种变量所有预测模型中表现最优，它的预测误差值最小，为0.187847。社会消费品零售额的MIDAS(3，6，1)-AR(1)模型次之，为0.273199。而固定投资完成额及出口的最优模型对应预测误差直分别是0.463540、0.620070。可初步说明，采用房地产投资数据作为高频解释变量明显改善了实时预测经济增长效果。为了观察房地产投资变量的整体实时预测效果，表6中计算了四种变量的包含高频数据五种不同滞后阶数模型的平均预测误差，显然，房地产投资预测误差平均值在四种变量中最小，为0.482559，社会消费品零售额次之，平均误差为0.490913。相较于固定投资完成额平均预测误差0.728978，以及出口平均预测误差0.805462，房地产投资预测平均误差大大减小。就此而言，房地产变量实时预测经济增长的效果整体上优于其他变量。

综上所述，本文认为利用房地产投资去实时预测GDP增长率是可行的，且相较于其他三种变量而言更具有效性。具体原因在于房地产投资涉及的产业众多，从开发、生产以及消费的过程中会产生一系列的经济效益，其中涉及到的产业链不断发展会间接影响消费、投资及就业，从而促进经济增长。当我国经济萧条、停滞不前时，政府往往通过加大房地产投资去拉动投资与需求的增长，从而达到拉动整体经济的目的；而当我国经济出现通货膨胀时，政府也会通过抑制房地产投资为经济降温。房地产投资与经济增长形成了相辅相成的关系，故其紧密相关，使用房地产投资指标能够精准的实时预测我国的经济增长。

（二）基于基准模型的实证分析。与混频模型对应，同频模型数据的时间应与其一致，相对于混频数据里的月度变量滞后6阶、9阶、12阶、15阶、18阶，这里令基准模型中的表示滞后期数的i分别为2、3、4、5、6。分别求出不同滞后阶数的RMSE与混频数据对应的值进行比较。具体如表7所示。

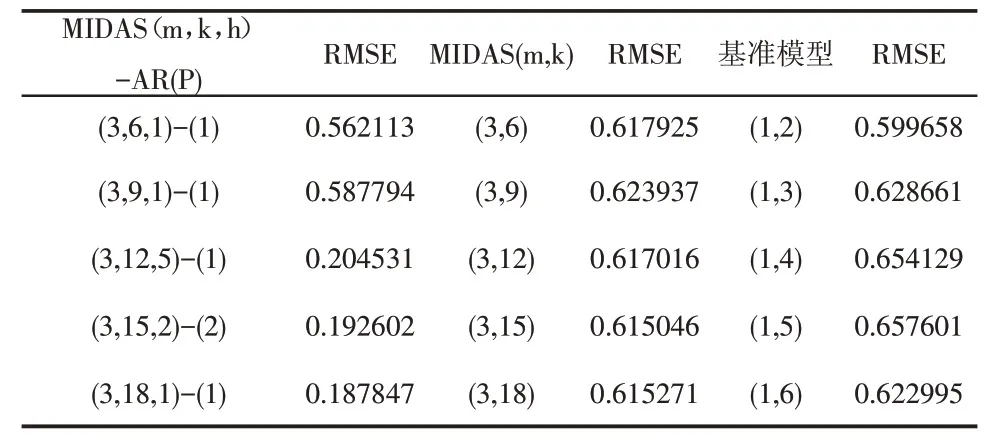
表7 房地产投资MIDAS与基准模型的比较

比较表7 中单变量MIDAS(m,k)模型（即模型（1））与同频基准模型（即模型（4））的RMSE值，显然，两者数值上较为相近，MIDAS(m,k)模型没有明显改善同频基准模型的预测效果。但观察加入向前预测并嵌入被解释变量自回归项的模型MIDAS(m,k,h)-AR(P)（即模型（3））的RMSE，将其与同频基准模型的RMSE 比较，显然MIDAS(m,k,h)-AR(P)大大减小了预测误差。譬如，高频解释变量滞后阶数为12，15，18时，相对应基准模型的RMSE 分别为0.654129，0.657601，0.622995，加入向前h 步预测及被解释变量自回归项的MIDAS(m,k,h)-AR(p)模型RMSE减少为0.204531，0.192602，0.187847。从另一视角来看，基准模型中最优模型对应RMSE 为0.599658（即滞后期 i 为 2 所对应模型），而 MIDAS(m,k,h)-AR(p)中最优模型MIDAS(3,18,1)-AR(1)对应的RMSE 为0.187847，可见预测效果明显改善。综上可知，与MIDAS(m,k)或同频基准模型相较而言，向前h步的自回归混频数据抽样模型作为一种实时预测手段，因其能充分利用最新数据的信息对预测结果进行修正，可令预测效果更优。

结语

本文构建了房地产投资变化率与GDP 增长率的向前h步预测的自回归混频数据抽样模型，并同时构建了社会消费品零售总额变化率、固定投资完成额变化率以及出口完成额与GDP增长率相应的混频数据抽样模型。通过比较每个变量不同滞后阶数对应的模型预测误差发现：

（1）在实时预测GDP 增长率时，房地产投资变化率的MIDAS(3，18，1)-AR(1)模型表现最优，误差仅为0.187847。且房地产投资变化率不同滞后阶数对应的模型预测误差平均值在四种变量中仍然最小。说明房地产投资变化率可精准的实时预测GDP增长率，及时的捕捉经济趋势变化，故可作为政策制定者判断经济趋势的主要参考依据。

（2）与相应的同频模型的精度相比，向前h 步预测的自回归混频数据抽样模型的精度大大提升。向前h 步预测的方法不仅可以预测样本外的数据，并可以充分利用最新发布的高频数据的信息去预测低频的被解释变量，保证了预测的时效性与精准性，因此混频数据抽样模型在实时预测方面效果更佳。

（3）利用房地产投资变化率并采用MIDAS(m,k,h)-AR(P)预测GDP增长率时，预测误差并不总是随着向前预测步数h的增大而增大，但向前1步预测时的房地产投资的预测效果均占优。当增加向前预测的步数时，往往会出现误差突然增大的情况，从这个角度来说，混频数据抽样模型用于房地产投资的实时预测（向前一步预测）预测效果更具稳健性。