钢框架结构梁柱节点重要性计算方法

栗云松，罗永峰，郭小农，李思宇，刘 俊

（同济大学土木工程学院，上海200092）

钢结构节点在使用过程中会出现损伤、锈蚀和材料性能退化等问题，导致节点承载力降低，进而引起结构整体刚度与承载性能退化，使得钢结构在使用过程中存在安全隐患。因此，对在役钢结构节点进行检测和鉴定是保障钢结构安全正常使用的必要条件。在实际工程中，结构节点数量较多，对全部节点进行检测成本较高，故一般采用抽样方法进行检测。抽样检测方法通常将节点划分为重要节点和一般节点，并对2类节点分别制定不同的抽样方案［1］：重要节点采用全部检测或严格的抽样检测方案，一般节点则采用相对宽松的抽样检测方案。重要节点和一般节点依据节点的重要性进行分类，因此，科学合理的节点重要性评定是保证节点检测抽样合理、结果准确可靠且经济的重要基础之一。

目前，节点重要性评定尚无成熟的方法与理论。现有的重要性评定方法主要有基于刚度的判定方法和基于能量的判定方法。基于刚度的判定方法［2-4］根据节点削弱或破坏前后结构整体刚度的变化判定节点的重要性，基于能量的判定方法［5-6］根据节点破坏前后结构总应变能的变化判定节点的重要性。然而，基于刚度和基于能量的重要性判定方法都仅考虑了节点削弱或节点破坏对结构整体性能的影响，并未考虑节点削弱或破坏实际发生的概率。

本文针对钢结构梁柱节点，将节点失效严重性和失效概率均作为评定参数，研究一种节点重要性计算方法。采用等效抗力折减系数作为节点失效的严重性评价参数、等效失效概率系数作为节点失效概率评价参数，综合考虑等效抗力折减系数和等效失效概率系数，并采用优劣解距离法（TOPSIS法）［7］计算节点重要性系数，进而判定节点重要性或进行节点重要性分类。

1 节点失效表征方法

1.1 节点失效模型

节点失效是指节点因性能退化以致无法传递荷载的现象。节点失效对结构整体承载力的影响是判断节点重要性的依据之一。梁柱节点失效可以分为2种类型［8］，一类为节点无法传递弯矩，但仍可以传递轴力和剪力，例如，梁柱栓焊节点的梁翼缘焊缝断裂而梁腹板仍由螺栓与柱连接，此时节点仅传递轴力和剪力；另一类为节点无法传递所有内力，例如全焊接节点焊缝破坏后，构件的轴力、剪力和弯矩均无法通过节点传递。针对上述2种梁柱节点失效类型，可采用以下2种方式进行模拟：①在结构计算模型中将节点与梁的连接变为铰接，如图1a所示；②在结构计算模型中断开节点与梁的连接，如图1b所示。

图1 节点失效模拟Fig.1 Simulation of failure of joint

1.2 失效严重性参数

节点失效将导致节点无法传递部分或全部构件内力，从而引起结构受力性能变化。不同的节点失效模式对结构整体承载能力影响不同，即节点失效后果的严重性不同。失效后果严重性是节点重要性评定的重要依据之一，因此，重要节点是失效后使结构整体承载能力明显降低的节点，即失效后果严重的节点。

钢框架结构失稳破坏是结构的主要破坏形式之一，结构极限稳定承载力是结构安全评定的重要指标。因此，用结构在节点失效前后极限稳定承载力的变化来描述节点失效的严重性，采用节点失效导致的结构极限稳定承载力的降低比例即承载力折减系数作为节点失效严重性评价参数。定义承载力折减系数为

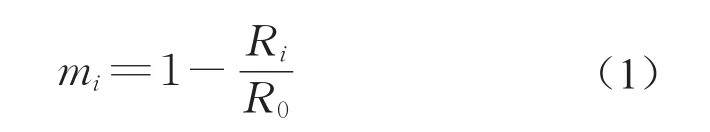
式中：mi为节点i的承载力折减系数；R0为完善结构的极限稳定承载力；Ri为节点i失效后的结构极限稳定承载力。

承载力折减系数mi最大为1，表示结构完全丧失承载能力；mi越小，节点失效对结构极限承载力影响越小；mi最小为零，表示节点失效对结构极限承载力无影响。

实际上，划分重要节点与一般节点是为了在保证检测可靠性基础上控制检测样本数量，优化检测成本，因此，同一结构不同节点的失效严重性的相对比较结果更具实际指导意义。据此，本文对承载力折减系数进行优化，提出可以统一量化节点失效严重性的等效抗力折减系数。对于具有N个节点的结构，计算得到N个节点分别对应的承载力折减系数，将其集合M表示为

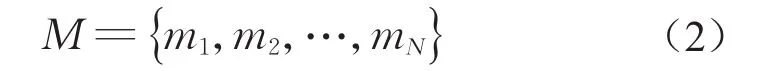
式中：m1、m2和mN分别表示第1、第2和第N个节点失效的承载力折减系数。

对集合M中的元素按数值大小进行降序排列，并记为m1′，m2′，…，mN′，其集合又可表示为

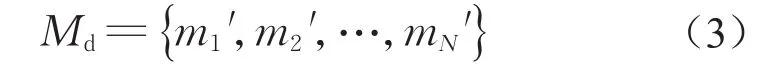
根据Md与M的对应关系，可以得到第i个节点的承载力折减系数mi在Md中的排序值，记为ri，则等效抗力折减系数定义为

式中：Iri表示在一个结构的全部N个节点中与其他节点相比较第i个节点失效的相对严重性。Iri越小，节点i失效的相对严重性越高。

1.3 失效概率参数

已有的关于节点重要性的研究中，多将节点失效的严重性作为重要性的唯一判断依据，未考虑节点的失效概率。对于一些失效严重性较高的节点，其失效概率可能很低，此时，仍将节点划分为重要节点是不合理的；而失效概率高的节点，即使严重性较低，也应当作为重要检测对象。因此，节点重要性划分应考虑节点的失效概率。

由于生产、制作和安装误差，实际钢结构的几何尺寸、材料性能等设计参数均存在一定偏差，这些偏差往往是随机的，并且，节点发生锈蚀、损伤等也具有随机性，这导致节点的抗力呈现随机性。同时，结构上的荷载及其他作用也是随时间变化的随机变量。节点的抗力和作用效应都具有随机性，因而节点抗力低于作用效应也是随机的，即节点失效是一个随机事件。同时，结构中部分节点失效会引起内力重分布，改变剩余节点的作用效应，使得各节点失效概率随之变化。因此，分析节点失效概率时，既应考虑影响抗力与作用效应的随机变量，还应考虑部分节点失效所引起的结构内力重分布。

由于结构系统的复杂性，节点失效概率难以直接进行理论求解，因而，采用蒙特卡洛方法［9］计算节点失效概率，作为节点重要性确定的依据。应用蒙特卡洛方法时，首先需要确定材料性能（如钢材的屈服强度、弹性模量等）、几何尺寸（如梁柱截面尺寸）、荷载（如地震作用、活荷载、恒荷载等）和节点损伤（如锈蚀深度）等随机变量的分布类型和分布参数，然后按照各随机变量的概率分布模型生成ns组随机数，进而按照该随机数建立ns个模型。当缺少节点损伤的统计数据时，可通过同等程度地削弱节点或增大荷载的方式来近似考虑节点损伤。

分析ns个模型之后，对于每个节点，可以获得ns个节点状态。若节点i发生ni次节点失效，则其失效概率系数为

式中：pi为节点i的失效概率；ns为蒙特卡洛模拟组数；ni为蒙特卡洛模拟中节点i失效的次数。

失效概率最大为1，表示该节点一定会失效。pi越小，节点失效的发生概率越小；pi最小为零，表示节点不会失效。

与导出承载力折减系数类似，对失效概率系数进行优化，提出可以统一量化节点失效概率的等效失效概率系数。对于具有N个节点的结构，计算得到N个节点分别对应的失效概率，其集合P为

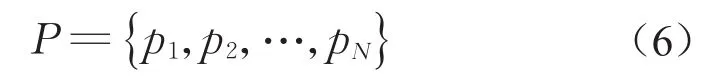
式中：p1、p2和pN分别表示第1、2和N个节点的失效概率系数。

将集合P中的元素按数值大小进行降序排列，并记为p1′，p2′，…pN′，则其集合又可表示为

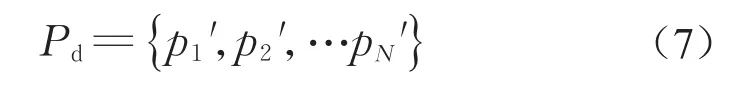
根据Pd与P的对应关系，可以得到第i个节点的失效概率系数pi在Pd中的排序值，记为bi，则等效失效概率系数定义为

式中：Ipi表示在一个结构的全部N个节点中，与其他节点相比较，第i个节点失效概率的相对大小。Ipi越小，节点i的失效概率相对越高。

2 节点重要性计算方法

将上述节点失效严重性和失效概率同时作为判定钢结构梁柱节点重要性的依据进行推导节点重要性的计算公式。其中，节点失效严重性采用等效抗力折减系数Iri表征，失效概率采用等效失效概率系数Ipi表征。

基于上述2个参数进行节点重要性的判定问题属于多属性决策问题，对于解决这类问题，目前TOPSIS法［7］是最广泛使用的方法之一。TOPSIS法首先构造多属性决策问题的理想解和负理想解，然后以评价对象与理想解和负理想解的距离作为参数，判断各评价对象的相对优劣。

采用TOPSIS法判断结构中各节点的相对重要程度时，可将参数Iri和Ipi组成有序数对（Iri，Ipi），进而将该有序数对作为评价对象，并构造关于（Iri，Ipi）的理想解和负理想解。理想解实际上就是节点失效严重性最大且失效概率最高的情况，即Iri=0且Ipi=0；负理想解就是节点失效严重性最小且失效概率最低的情况，即Iri=1且Ipi=1。因此，TOPSIS法就是根据各节点的（Iri，Ipi）与理想解（0，0）和负理想解（1，1）的距离大小关系评价节点的重要性。

节点的（Iri，Ipi）与理想解的距离Di+和与负理想解的距离Di—可采用下式计算：

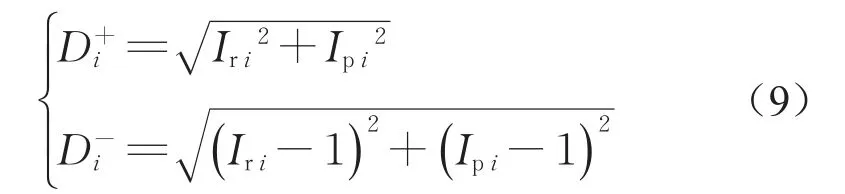
根据式（9）计算得到Di+和Di—后，可计算相对接近度IMi。

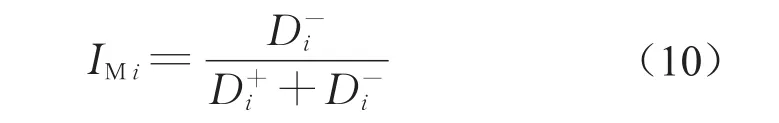
由式（10）可知，IMi越大，节点的（Iri，Ipi）与理想解的距离越近，与负理想解的距离越远，表明该节点越重要。因此，将相对接近度IMi定义为节点重要性系数，用于计算结构中节点的相对重要性。

采用IMi计算节点重要性系数，可以综合考虑节点失效严重性和失效概率，既能对失效严重性较高的节点进行有效判定，也能对失效概率较高的节点进行有效判定。

3 算例

以某钢框架结构为例来计算节点重要性。该结构横向总长24m，纵向总长18m，地上3层，层高均为4m，总高12m，共64个梁柱节点，结构布置如图2所示。工程所在地区抗震设防烈度为7度，设计基本地震加速度为0.08g。框架梁截面为H500×200×10×16（单位：mm），柱截面为H300×300×10×15（单位：mm），梁柱节点为全焊接节点，如图3所示。构件均采用Q235钢材，钢材的本构模型采用双折线模型，弹性模量E=2.06×105MPa，屈服强度fy=235MPa，强化段弹性模量为Ey=790MPa。节点计算模型采用强化双线性分析模型［10］，其弯矩-转角曲线中的相关参数按照欧洲规范［11］建议公式计算得到，其中初始刚度Sj=9.77×107kN·m·rad-1，节点抗弯承载力Mu=450.71kN·m，如图4所示。

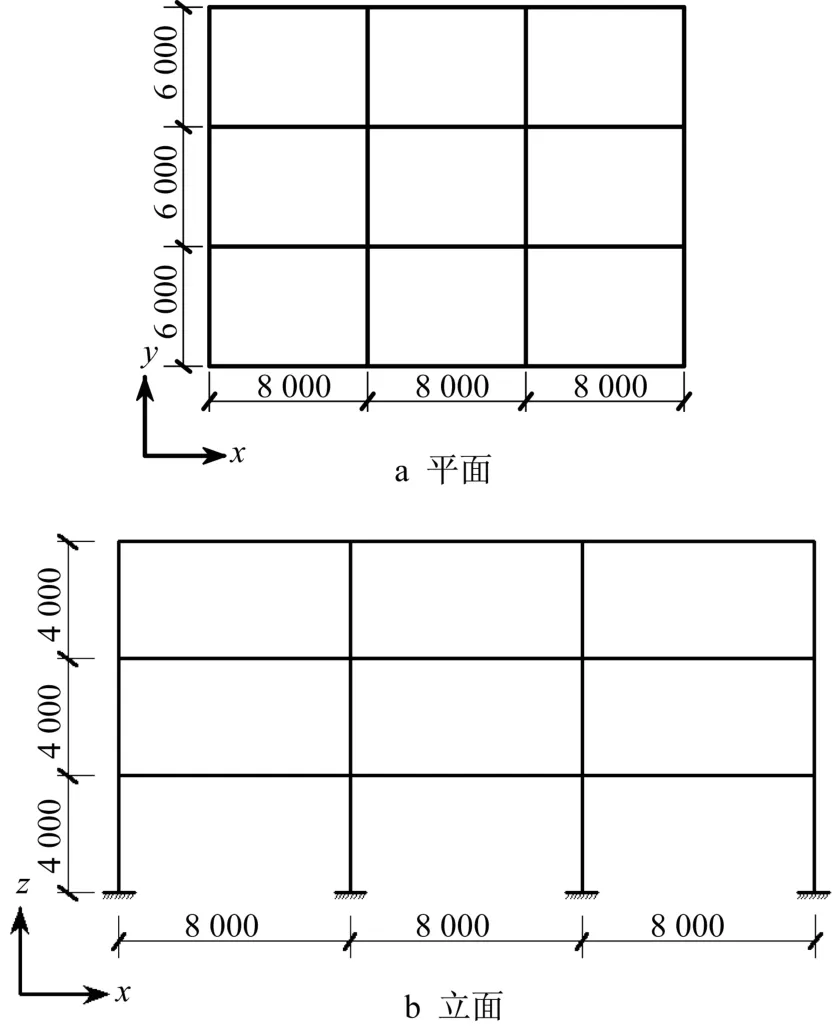
图2 钢框架结构布置（单位：mm）Fig.2 Layout plan of steel frame structure（unit：mm）

采用ANSYS软件建立有限元模型，梁和柱均采用Beam188单元模拟，节点采用Combin39扭转弹簧单元模拟，有限元模型如图5所示。各层楼面荷载相同，恒荷载标准值（SG）为5.0kN·m-2，活荷载标准值（SQ）为2.0kN·m-2，地震作用标准值（SEh）仅考虑水平地震作用，且采用底部剪力法确定［12］。重力荷载代表值（SGE）取值为1.0SG+0.5SQ。模型计算所考虑的荷载组合为1.2×SGE+1.3×SEh。

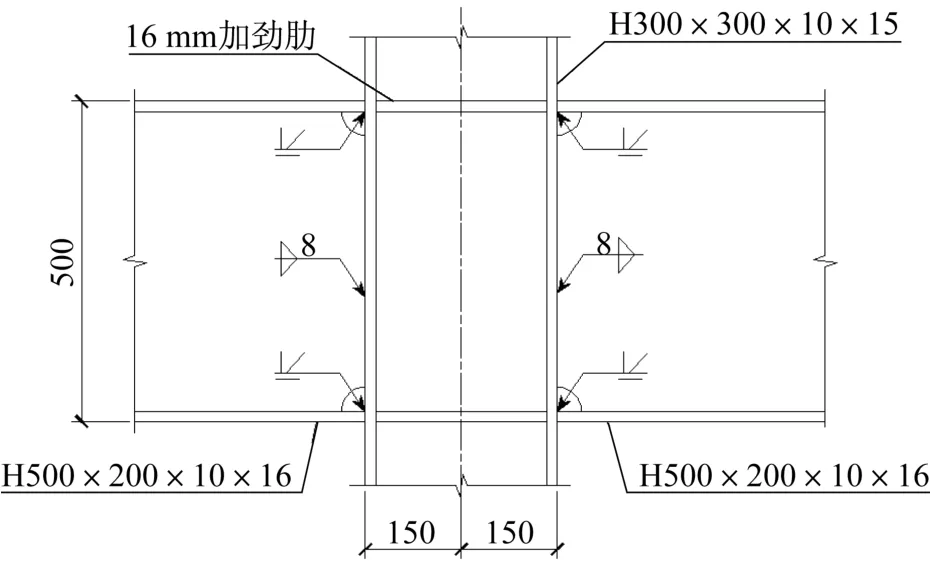
图3 梁柱节点详图（单位：mm）Fig.3 Detail drawing of beam-column joints（unit：mm）

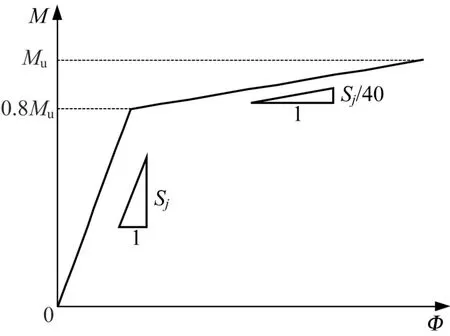
图4 梁柱节点弯矩与转角关系Fig.4 Moment-rotation curves of beam-column joints

全焊接节点的失效类型为焊缝破坏，节点失效后无法传递所有内力。因此，在计算节点等效抗力折减系数时，以移除节点与梁的连接的方式模拟节点失效；在计算等效失效概率系数时，通过生死单元法模拟节点失效，即当节点弯矩达到极限弯矩Mu时，在有限元模型中移除模拟节点的弹簧单元。

对图5中结构节点采用有序数对（u，v，w）进行编号，其中，u表示x方向第u个节点、v表示y方向第v个节点、w表示z方向第w个节点，x、y、z方向如图5所示。计算得到的梁柱节点的等效抗力折减系数Iri如表1所示。

表1表明，在高度方向上，第3层的梁柱节点的等效抗力折减系数较小，即顶层的梁柱节点失效对结构极限承载力的影响较大；在楼层范围内，中柱的等效抗力折减系数较小，即中柱节点失效对结构极限承载力的影响较大；整个框架结构中失效严重性最大的节点基本位于第3层的中柱部分。

图5 钢框架结构有限元模型Fig.5 FE model of steel frame structure

在计算节点的等效失效概率系数时，算例共考虑8种随机变量，各变量的分布类型及分布参数［13-14］见表2。当随机变量取不同值时，节点的初始刚度Sj和极限承载力Mu也相应变化，每组样本计算时根据数据不同重新计算节点刚度及节点抗弯承载力。样本容量取ns=10 000，即根据表2中各随机变量的分布生成10 000组随机数，作为算例中蒙特卡洛方法的计算样本。计算分析得到结构各节点的等效失效概率系数Ipi如表3所示。

表1 等效抗力折减系数Tab.1 Equivalent resistance reduction coefficient

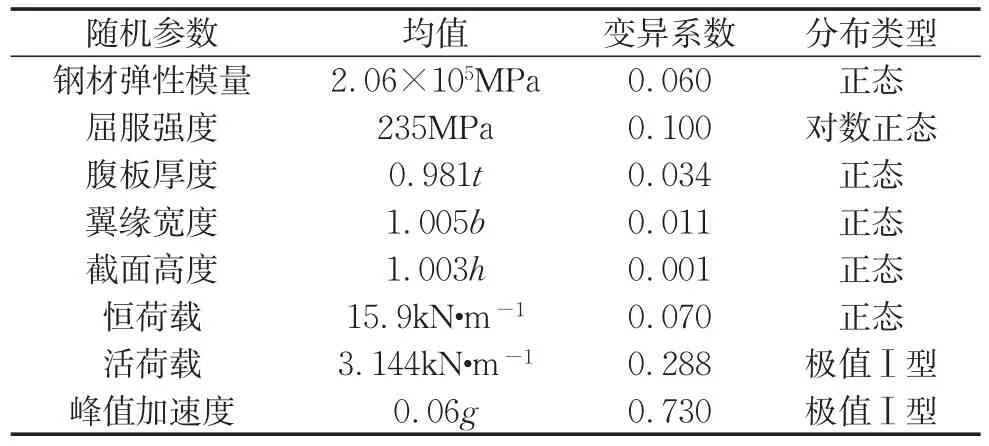
表2 随机变量分布Tab.2 Distribution of random variables

表3表明，在高度方向上，首层的梁柱节点的等效失效概率系数较小，即首层节点失效的实际发生的概率较大；在楼层范围内，中柱节点的等效失效概率系数较小，即中柱节点失效实际发生的概率较大；整个框架结构中失效概率最大的节点基本位于首层的中柱部分。

为判定各节点的重要程度，计算得到各节点的重要性系数IMi，如表4所示。同时，将重要性系数最大的16个节点标记于结构中，如图6所示。

表4和图6的结果表明，在高度方向上，第1层和第3层梁柱节点的重要性较高；在楼层范围内，中柱节点的重要性较高；整个框架结构中节点重要性最高的16个节点基本位于首层及第3层。由于算例仅针对单一荷载模式下的纯框架进行分析，并未进行应力比优化设计，因而，该模型梁柱节点的等效抗力折减系数、等效失效概率系数和重要性系数可能与实际结构有所不同。

表3 等效失效概率系数Tab.3 Equivalent failure probability coefficient

表4 重要性分类指标Tab.4 Importance measure index

图6 重要性系数最高的16个节点Fig.6 16 joints of the highest IMi

4 结论

（1）采用节点失效所导致的结构极限承载力的降低比例定义了承载力折减系数。进而，基于同一结构各节点失效的相对严重性将承载力折减系数统一量化为等效抗力折减系数，并将其作为节点失效严重性的评价参数。

（2）节点的失效概率可采用蒙特卡洛方法计算得到。进而，基于同一结构各节点失效概率相对大小，将失效概率系数统一量化为等效失效概率系数，并将其作为节点失效概率的评价参数。

（3）基于等效抗力折减系数和等效失效概率系数，采用TOPSIS决策方法，提出钢框架结构梁柱节点重要性系数的计算方法，并给出了数值算例。结果表明：所提出的节点重要性系数计算方法能定量识别框架结构系统中的重要节点。但该算例仅针对单一荷载模式下的纯框架进行分析，还需要进一步研究不同结构类型及不同荷载组合下的梁柱节点重要性。