考虑安全性的桥梁主梁体系可靠性动态藤Copula预测

樊学平，杨光红，肖青凯，刘月飞

（1.兰州大学西部灾害与环境力学教育部重点实验室，甘肃兰州730000；2.兰州大学土木工程与力学学院，甘肃兰州730000）

桥梁健康监测（bridge health monitoring，BHM）系统的研制与开发已处于相对成熟阶段，并且在长期运营过程中积累了大量监测数据。然而如何有效分析和处理这些数据，进而建立桥梁结构的可靠性评定和预测方法，在国内外还处于研究的起步阶段，但已成为BHM领域的主要科学问题和共识问题。

国外，Frangopol等［1-2］首次给出基于监测数据的桥梁体系可靠度评估的基本框架流程，并将其应用于工程实例，分析中假定构件失效模式相互独立。Dissanayake等［3］采用监测数据，假定构件失效模式相互独立，分析了一座旧桁架桥的体系可靠性。Pourali等［4］提出一种新的传感器优化布置方法，并在此基础上亦假定构件失效模式相互独立，进行结构体系可靠性的监测研究。ZHANG等［5］基于Copula理论研究了退化桥梁的损伤因子评估研究。JIANG等［6］利用Copula技术深入分析了失效相关的结构体系时不变可靠性。国内，焦美菊和孙利民等［7］研究了结构健康监测与可靠度评估相结合的桥梁构件性能评估方法。陈志为［8］基于结构健康监测系统提出了大跨多荷载悬索桥关键位置的疲劳可靠度分析框架，并应用于香港青马大桥。LIU等［9］利用Copula函数建立了疲劳应力和疲劳应力环之间的相关性模型，进而进行了正交异性钢桥面的疲劳可靠性评估.樊学平［10］基于监测数据，采用贝叶斯动态模型和粒子滤波器，亦假定失效模式相互独立，研究分析了天津富民桥的体系时变可靠性.LIU等［11-13］基于结构健康监测数据，初步假定2个监测点失效非线性相关，研究了长春伊通河桥主梁的动态可靠性预测方法.张建仁等［14］深入研究退化钢筋混凝土梁受弯和受剪2种失效模式的相关性，进而分析了梁时变可靠性。刘扬等［15］分析了验证模式和失效模式间的相关性对结构可靠性的影响规律。王向阳等［16］采用Copula技术分析了连续梁桥的失效非线性相关的时不变可靠性。LIU等［17-18］研究了桥梁体系失效时不变非线性相关的时不变可靠性分析方法，并在此基础上给出了主梁体系2个监测点的时变非线性相关性的Copula建模方法，分析了主梁体系的动态可靠性［13，19］；刘月飞等［20］研究了基于藤Copula的桥梁主梁体系时不变可靠性分析方法。Li等［21］研究了基于D-vine Copula模型的高架桥地震易损性评估分析。

由上述研究现状可知：桥梁可靠性研究主要集中在以下6个方面：①桥梁构件可靠性分析；②构件失效模式相互独立的桥梁体系可靠度分析；③考虑失效模式之间和失效模式与验证模式之间线性相关性的桥梁可靠度分析；④仅考虑2个失效模式非线性相关的桥梁时不变可靠性分析；⑤基于藤Copula的多个失效模式非线性相关的桥梁体系时不变可靠性分析；⑥仅考虑2个失效模式时变非线性相关性的桥梁构件时变可靠度分析。而基于藤Copula模型的多个失效模式时变非线性相关的桥梁体系动态可靠性预测还未展开大量研究。考虑在役桥梁主梁体系含有多个监测点，且具有相同的输入随机荷载和环境源，因而这些监测点的失效模式之间存在动态非线性相关性［22］。因此，利用在役桥梁动态监测数据建立主梁体系监测点失效模式之间的时变非线性相关性模型进而动态预测考虑安全性的在役桥梁主梁体系可靠性需要进一步展开研究。

鉴于上述存在的问题，以在役桥梁主梁体系为研究对象，主梁截面多个危险监测点的监测变量形成一个随机场，考虑到随机场动态监测数据的随机性和相关性的特点，定义动态监测数据是具有相关性的随机时间序列，利用桥梁健康监测数据建立在役桥梁主梁多个监测点失效模式间的时变非线性相关性模型，进而预测桥梁主梁体系动态可靠性。具体步骤为：首先，建立贝叶斯动态线性模型（Bayesian dynamic linear model，BDLM）和藤Copula技术相融合的描述随机场动态非线性相关性的贝叶斯动态藤Copula模型（BDVCM）；然后，结合一次二阶矩（FOSM）方法，预测考虑失效模式动态非线性相关性的在役桥梁主梁体系动态可靠性；最后，利用天津富民桥主梁体系监测极值应力数据进行验证分析。

1 随机场BDVCM的建模

采用日常极值应力为监测变量，主梁的多个监测变量形成一个随机场。首先采用历史日常监测极值应力数据建立主梁随机场的BDLM，实现日常极值应力的动态预测；然后建立主梁随机场非线性相关性的藤Copula模型；最后建立BDLM和藤Copula技术相融合的BDVCM。流程见图1。

1.1 随机场DLM及其贝叶斯概率递推

1.1.1 构建DLM

随机场包含多个监测变量，采用动态监测数据对在役桥梁主梁体系随机场中监测变量进行DLM（dynamic linear model）建模分析，包括观测方程、状态方程以及初始状态信息。观测方程为

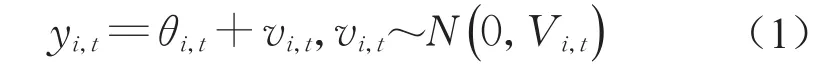
状态方程为

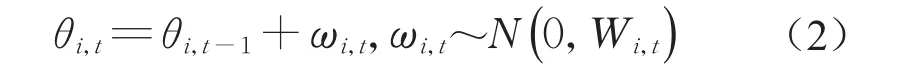
初始状态信息为

图1 BDVCM的建模流程图Fig.1 Modeling processes of BDVCM

式中：yi，t、vi，t以及ωi，t分别为t时刻第i个监测变量的观测值、观测误差以及状态误差；N(·)为正态概率密度函数（probability density function，PDF）；θi，t为t时刻第i个监测变量的状态值；Vi，t为t时刻第i个监测变量的监测误差的方差；Wi，t为t时刻第i个监测变量的状态误差的方差；Di，t={yi，t，Di，t-1}，Di，t为第i个监测变量在t时刻及以前的系统的信息集，包括mi，t（平均值）、Ci，t（方差）等。假设vi，t，ωi，t各自独立且相互独立，且均与θi，t独立。

1.1.2 DLM的贝叶斯概率递推

t—1时刻的状态后验PDF为

t时刻的状态先验PDF为

式中：ai，t=mi，t-1；Bi，t=Ci，t-1+Wi，t。

t时刻观测变量的一步预测PDF为

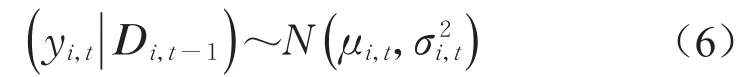
t时刻的状态后验PDF为

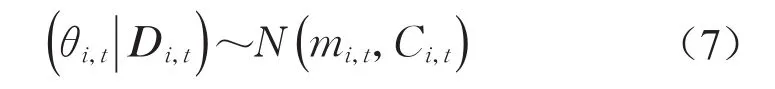
根据HPD（highest posterior density）区域的定义［23-24］，观测值含有95%保证率的一步预测区间为I。

1.1.3 DLM主要参数的确定

DLM贝叶斯更新时间间隔为1d，主要参数有Vi，t、Wi，t、mi，t、Ci，t。对t时刻以及之前的监测数据进行五点三次平滑处理，得到t时刻的初始状态信息集，对初始状态信息进行概率统计及参数估计，可得mi，t、Ci，t以及Vi，t。状态误差方差Wi，t可利用式（9）近似确定［23-24］：

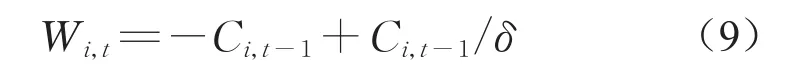
式中：δ为折扣因子，一般取0.98［10］。

1.2 随机场的藤Copula模型

1.2.1 Copula理论

根据Sklar定理［25］可知，若F是随机场中n维随机变量x=(x1，x2，…，xn)的连续联合概率分布函数（CDF），对应的连续边缘CDFs分别为F1，F2，…，Fn，则存在Copula函数C，对任意的x=(x1，x2，…，xn)∈ Rn，有式（10）和（11）成立。

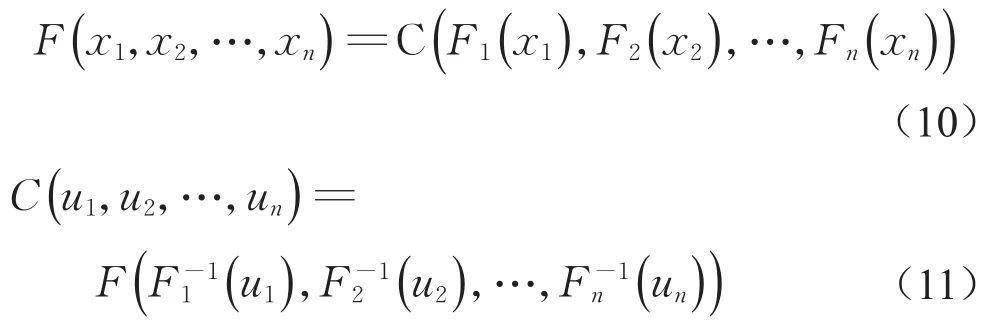
式 中 ：ui=Fi(i=1，2，…，n)，(u1，u2，...，un)=u，是Fi的广义逆函数。

由 式（10）可 得x=(x1，x2，…，xn)的 联 合PDF为

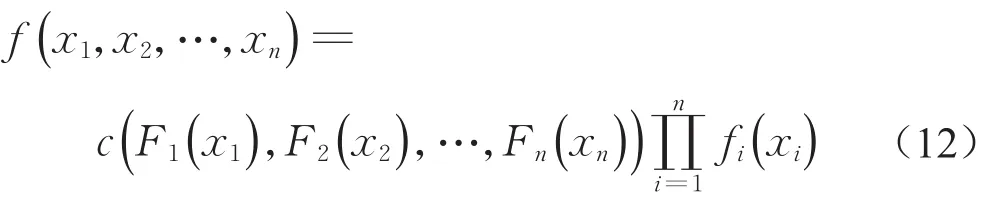
式中：fi(xi)为边缘PDF；c(u)为Copula联合PDF。

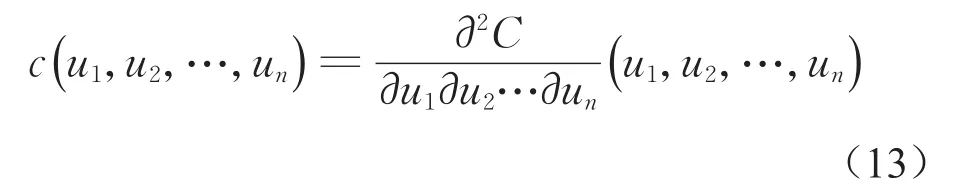
由概率积分变换［25］可知，随机变量Ui≡Fi(Xi)，i=1，2，…，n服从（0，1）均匀分布且因此，式（11）可以写成：

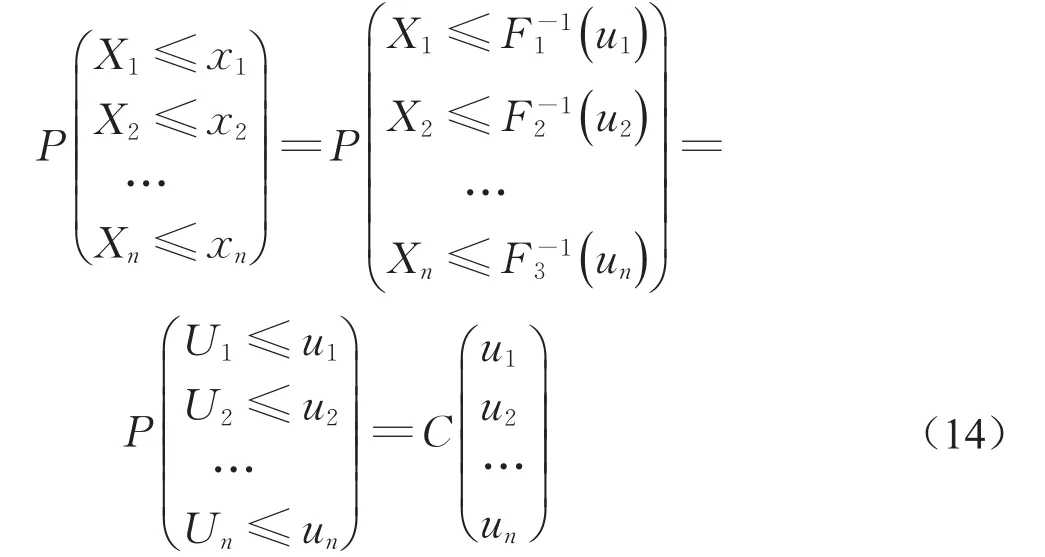
1.2.2 随机场中5维藤Copula结构

广泛应用的藤结构［25］主要包括C藤和D藤。以随机场中5维监测向量为例，结合C藤和D藤建立藤Copula模型，如图2和图3所示，图中(1，2，3，4，5)=(x1，x2，x3，x4，x5)，ij表示xi与xj形成的 Pair-Copula函数；ij|k表示在xk已知的条件下，xi与xj形成的Pair-Copula函数；ij|kl表示在xk与xl已知的条件下，xi与xj形成的Pair-Copula函数；ij|klm表示在xk、xl以及xm已知的条件下，xi与xj形成的Pair-Copula函数。

图2为5维C藤Copula结构分析图，该藤结构有4棵树，每棵树有1个主节点，每个主节点均连接到其他节点上，每条连接主节点与其他节点的边对应1个Pair-Copula模块。图3为5维D藤Copula结构，含有4棵树、10条边，对应10个Pair-Copula模块。C藤或D藤结构中不同边相互独立，对应不同的Pair-Copula PDFs。

图2 5维C藤Copula分解结构Fig.2 Structure of five dimensional C-Vine Copula

1.3 随机场的BDVCM

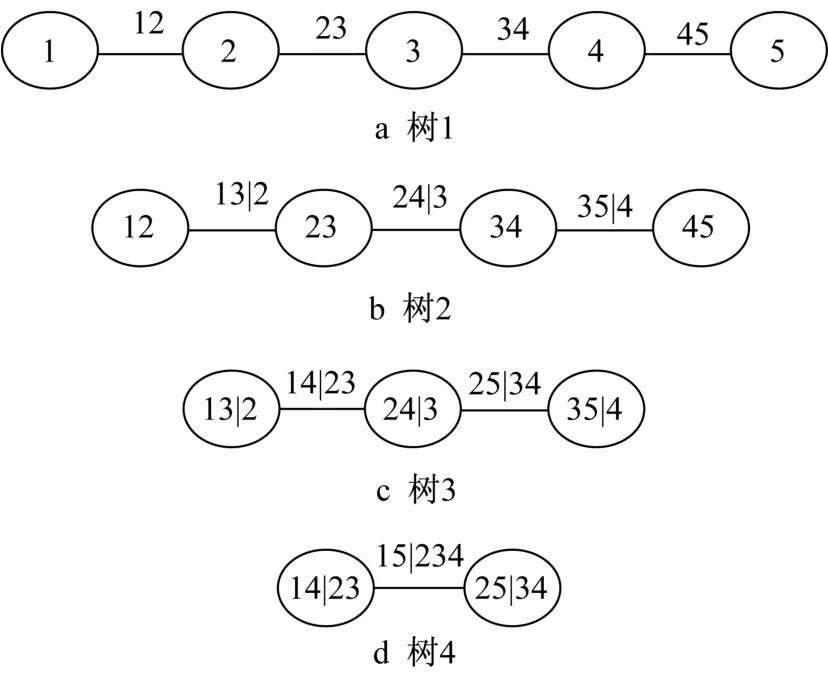
图3 5维D藤Copula分解结构Fig.3 Structure of five dimensional D-Vine Copula

BDVCM由贝叶斯方法、DLM以及藤Copula模型融合而成。随机场的多元联合分布分解成一系列两两监测变量间的Pair-Copula模块，然后用边连接起来，并结合DLM的贝叶斯递推过程，即可得到BDVCM。

基于动态监测数据可得随机场的皮尔逊线性相关系数，采用式（20）可得Copula模型的动态相关参数［13，19］，进而将 2 个监测变量的一步预测 PDF 和Gaussian Copula函数相结合，即可得二元监测变量的动态Pair-Copula模块［20］，进而将建立的动态Pair-Copula模块和藤结构进行合成，即可得到贝叶斯动态藤Copula模型（BDVCM）。

由式（6）可知，2个监测变量的一步预测变量分别为y1，t+1和y2，t+1，且均服从高斯分布，即

利用式（15）～（17），可得动态Pair-Copula函数，如式（18）～（19）所示：

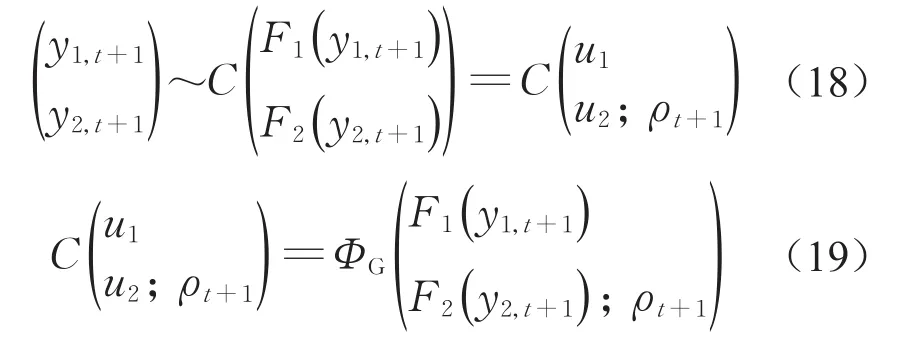
式中：ρt+1为动态Pair-Copula函数的时变相关参数，可由式（20）计算得到；ΦG(·)为 Gaussian Copula函数。

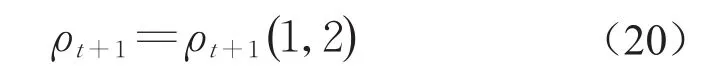
式中：ρt+1(1，2)为随机场中任意2个监测变量之间的动态皮尔逊线性相关系数。

C藤或D藤将随机场中两两监测变量间的动态Pair-Copula模块连接起来，即可得到BDVCM。

2 失效动态非线性相关的在役桥梁截面动态可靠性预测

2.1 动态可靠性预测流程

基于1.3节所建立的刻画监测变量动态非线性相关性的BDVCM，利用两两监测点失效模式间的动态Pair-Copula模块，通过Vine结构来建立多个监测点失效模式的动态非线性相关性模型，进而可实现失效动态非线性相关的主梁体系动态可靠性分析，核心流程如图4所示。详细步骤为：①基于容许应力和各个监测点动态预测的极值应力信息，采用FOSM方法，动态预测各监测点的可靠指标和失效概率；②基于各监测点动态预测的失效概率，采用Pair-Copula理论，进行仅有2个监测点且其失效动态非线性相关的主梁可靠性预测分析；③基于两测点失效动态非线性相关的主梁可靠性预测结果，采用串联体系可靠性分析方法，进行含有多个监测点且其失效模式相互动态非线性相关的主梁体系可靠性预测分析。

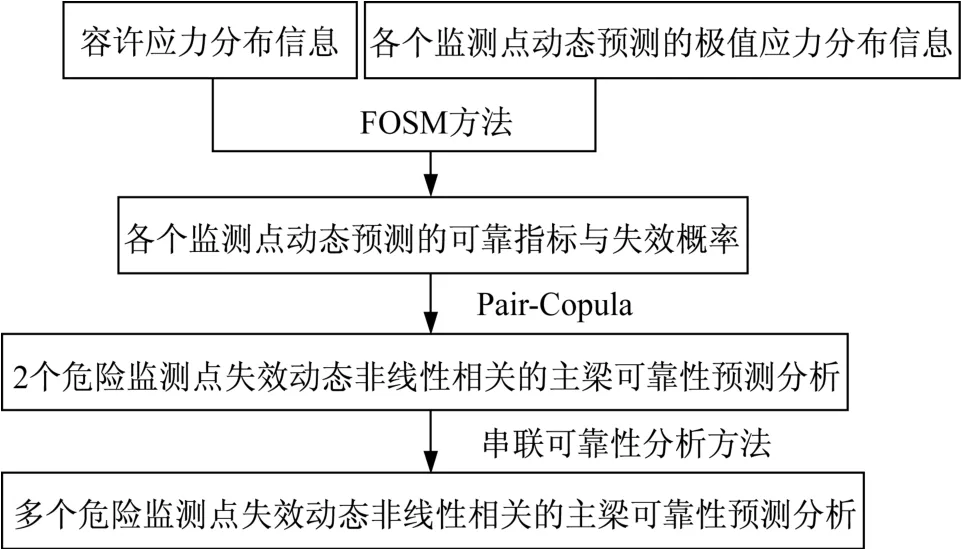
图4 主梁可靠性预测流程Fig.4 The flowchart of dynamic prediction for main girder reliability

2.2 危险监测点的可靠指标公式

通过主梁随机场的监测极值应力，研究考虑安全性的主梁体系可靠性，采用的桥梁截面危险监测点极限状态方程为

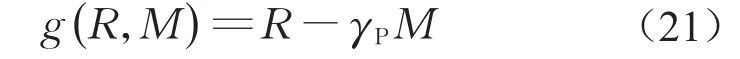
式中：R为钢材屈服强度；M为预测的日常极值应力；γP=1.15为传感器修正系数［10］。

采用式（21）和FOSM方法［26-27］可得监测点动态预测的可靠指标为

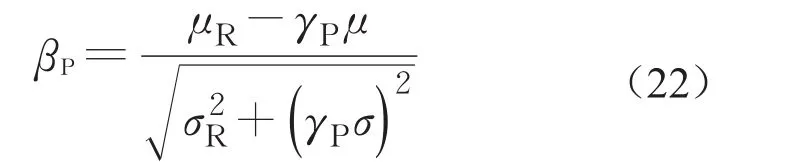
式中：μ、σ为监测变量BDLM的一步预测平均值与标准差；μR、σR为钢材屈服强度的平均值和标准差。

2.3 基于随机场BDVCM的桥梁截面动态可靠性预测

由文献［13，19］可知，任意2个监测点失效模式对应的功能函数如式（23）所示，2个失效模式同时发生的概率如式（24）所示。

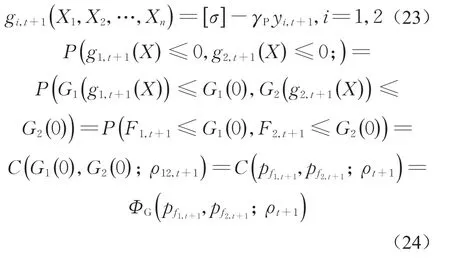
利用串联结构体系可靠性分析方法，多个测点失效时变非线性相关的考虑安全性的主梁截面动态可靠性预测可由式（24）来计算，并取其中2个测点失效同时发生的概率的最大值。

3 算例分析

天津富民桥设计为单塔空间索面自锚式悬索桥。采用该桥梁横桥向5个截面（A、B、C、D、E截面）的监测数据进行验证分析［10，22］，监测极值应力数据由车辆荷载以及温度荷载等耦合产生。截面位置如图5所示。主梁采用Q345qD钢材，其屈服强度为345MPa，变异系数为 0.098［28］，屈强比不大于0.84［29］，进而可得容许应力及其变异系数分别为411MPa和0.098。截面传感器布置如图6所示。每个截面均含有3个监测点，其中截面A监测点安装的传感器分别为FBG01074、FBG01081、FBG01078；截面B监测点安装的传感器分别为FBG01947、FBG01949、FBG01946；截面C监测点安装的传感器分别为 FBG01059、FBG01071、FBG01073；截面D监测点安装的传感器分别为FBG01012、FBG01015、FBG01005；截面E监测点安装的传感器分别为FBG01029、FBG01021、FBG01028。5个截面属于串联关系。

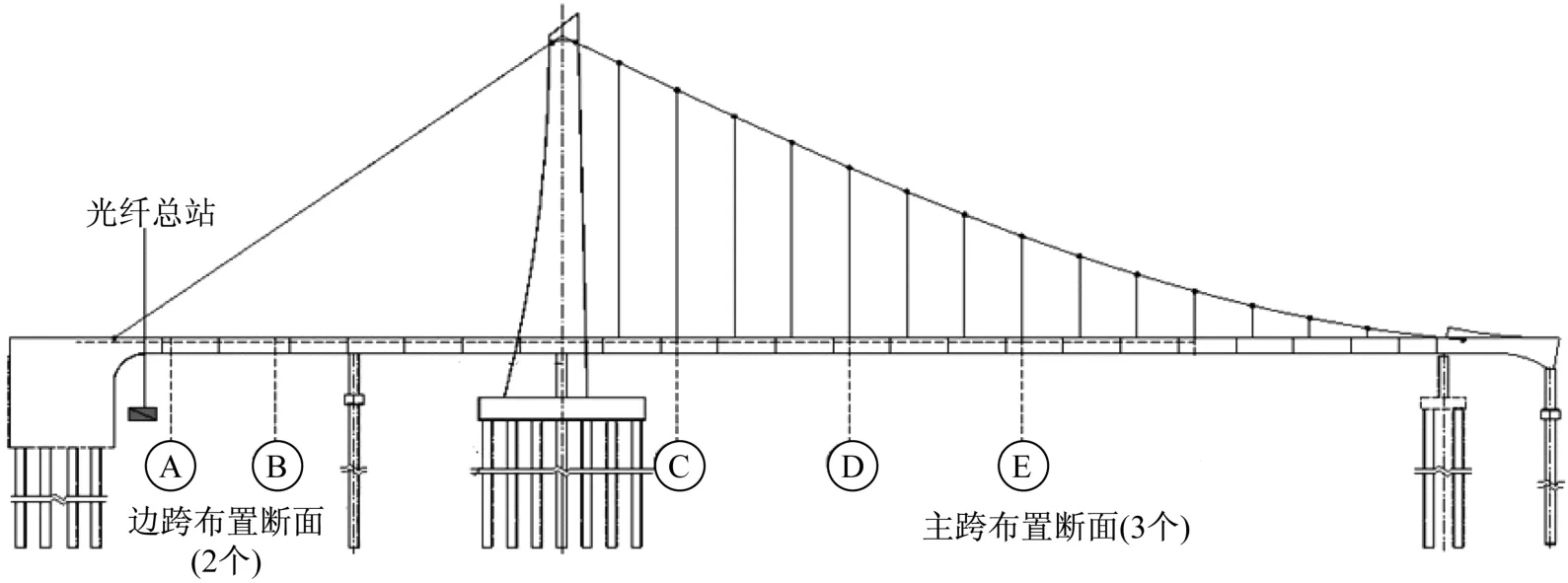
图5 富民桥主梁监测截面分布Fig.5 The layout of the monitored sections about Fumin bridge girder

3.1 截面日常极值应力数据

对天津富民桥主梁横桥向5个截面的日常极值应力进行了200d的监测，可正确提取监测信号的概率统计特性。每个截面的3个监测点中选取日常最大应力绝对值作为该截面极值应力数据。5个截面的监测极值应力时程曲线如图7所示。

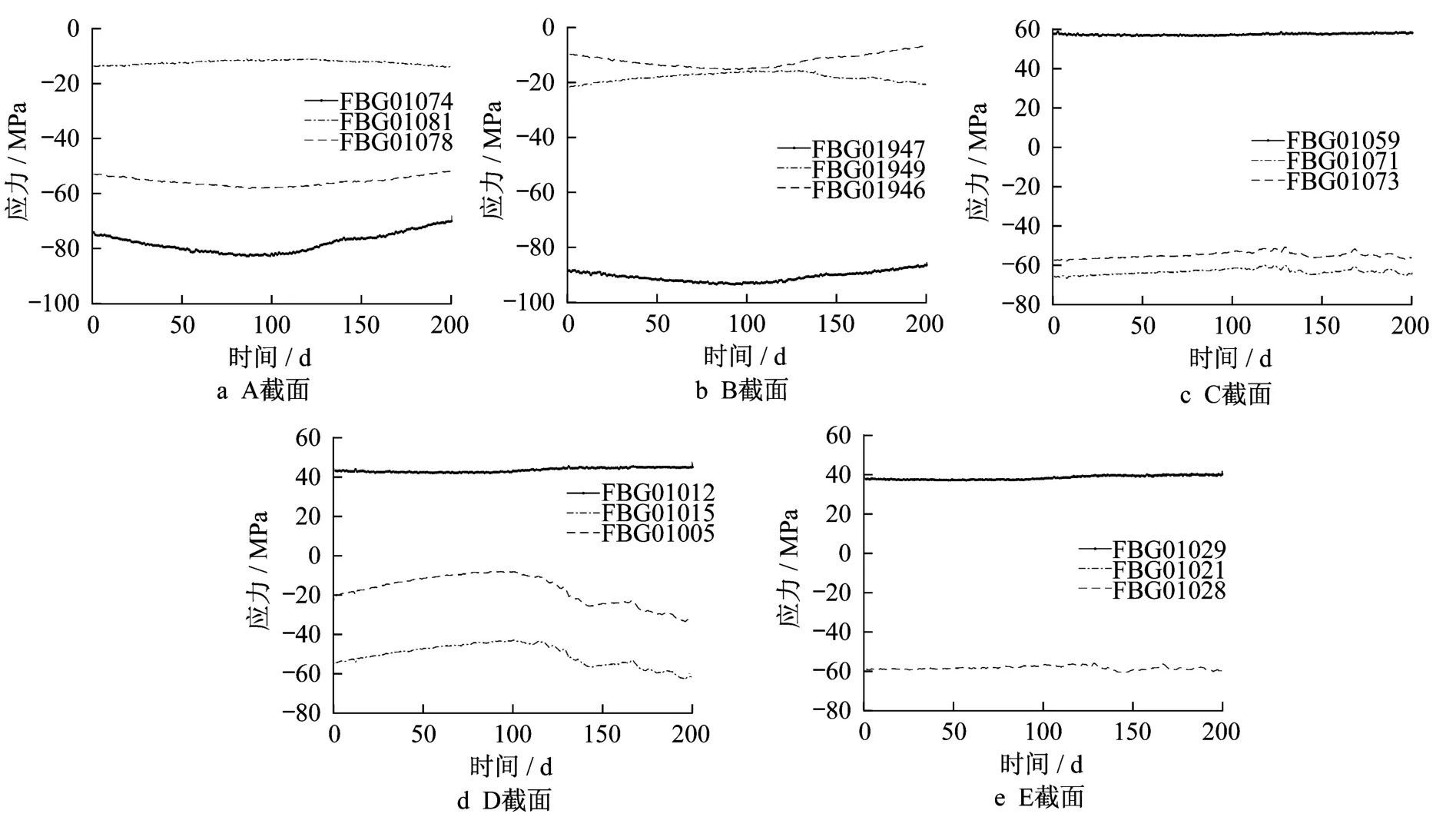
图7 5个截面的监测应力Fig.7 Monitoring stresses of five sections

3.2 截面极值应力DLM建模及贝叶斯动态预测

5个截面所对应的监测极值应力（监测变量）形成一个随机场，分别对对应极值数据进行五点三次平滑处理，处理后的数据被认为是DLM的初始状态数据。由式（1）～（3）可得5个截面的极值应力的DLMs。观测方程为

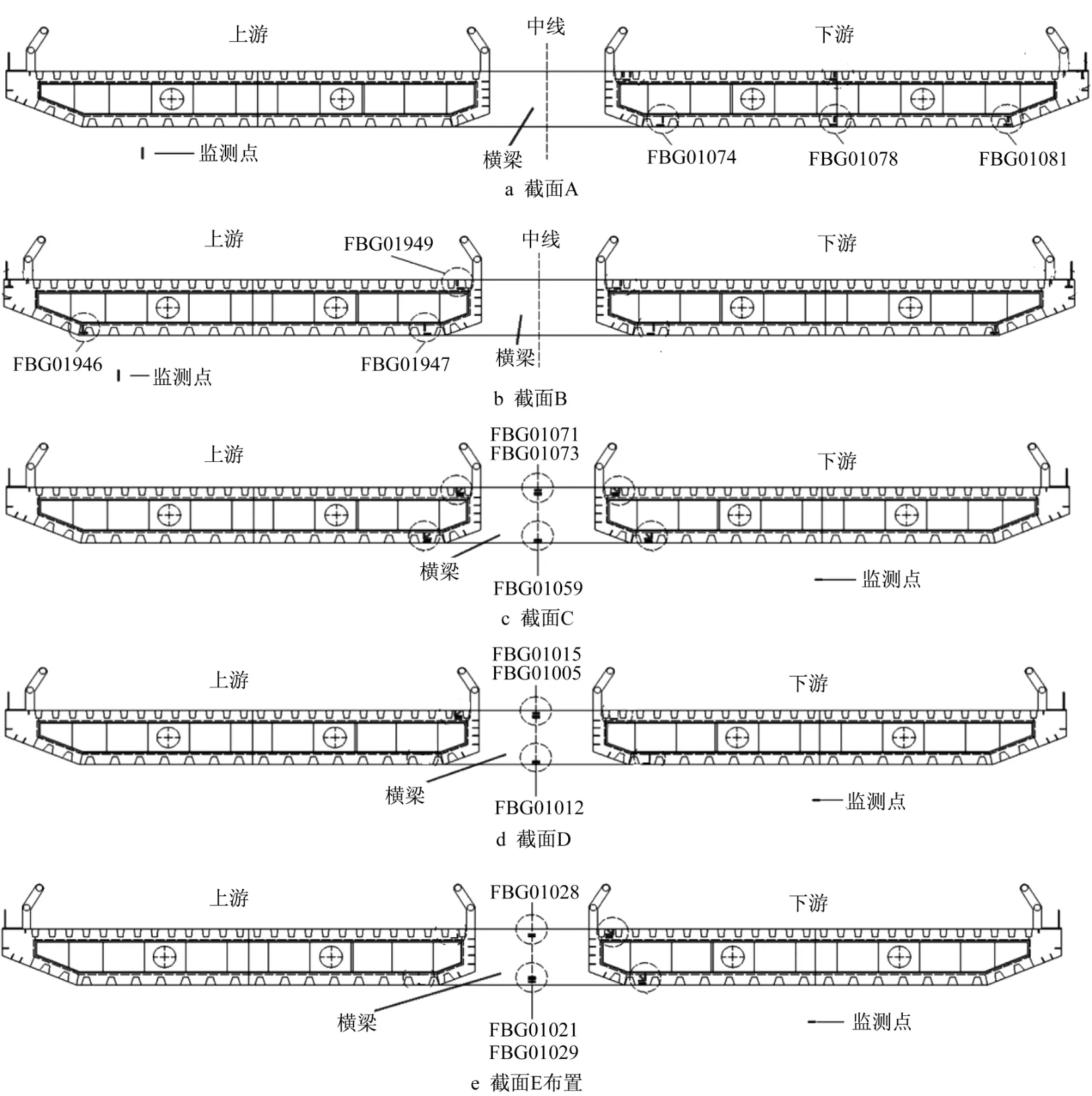
图6 5个截面的传感器Fig.6 The sensor layouts for five sections

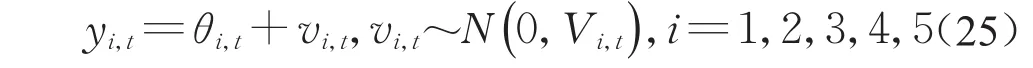
状态方程为

对A、B、C、D、E截面的初始状态信息进行Kolmogorov-Smirnov检验，可得5个截面的初始状态信息均服从正态分布，如式（27）所示。

Vi，t可由动态监测极值应力数据和初始状态信息进行估计。Wi，t可由式（28）得到。

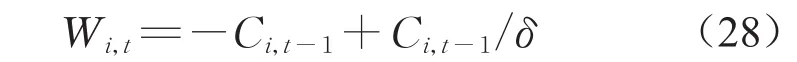
式中δ取0.98。

由式（27）可知，主梁随机场的极值应力均服从正态分布，故采用DLM的贝叶斯动态递推过程对随机场5个监测变量的动态极值应力进行预测，如图8所示。由图可知，A、B、C、D、E截面监测极值应力的预测结果能够合理反映5个截面动态监测极值数据的变化范围和趋势。

3.3 桥梁主梁体系的时变可靠性预测分析

3.3.1 不考虑危险监测点失效模式相关性的时变可靠性预测

采用FOSM方法［26-27］动态预测天津富民桥主梁截面最危险点的可靠性。该桥钢材容许应力服从均值为411MPa、变异系数为0.098的正态分布［10，28］。

结合式（22）可得最危险监测点考虑安全性的动态预测的可靠指标为

结合DLM的贝叶斯动态递推过程分别对5个截面的最危险点可靠指标进行预测，且与5个截面实时监测的可靠指标进行对比分析，结果如图9所示。由图9可知：融合采用DLM和FOSM方法所得的结果能够反映动态监测可靠指标的变化范围和趋势。

图8 5个截面极值荷载效应的预测值Fig.8 Predicted extreme load effects of five sections

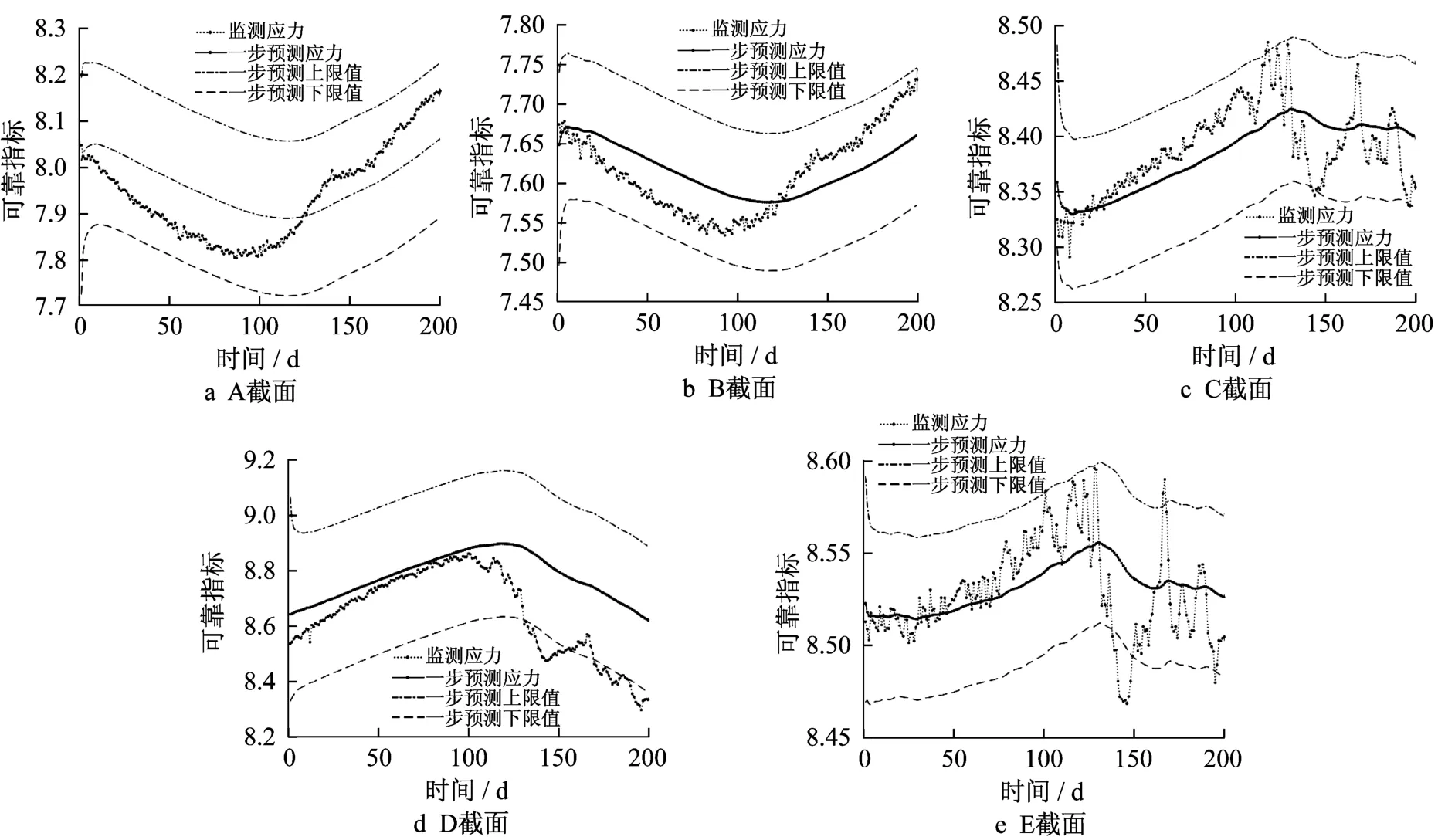
图9 5个截面可靠指标的预测值Fig.9 Predicted reliability indices of five sections

对5个截面最危险监测点的动态可靠指标进行对比分析，选取最小值作为该主梁体系的不考虑失效模式相关性的时变可靠指标，如图10所示。由式pf=Φ(-β)计算可得主梁体系时变失效概率。对5个截面的失效概率进行对比分析，选取最大值作为该结构体系不考虑失效模式相关性的时变失效概率，如图11所示。

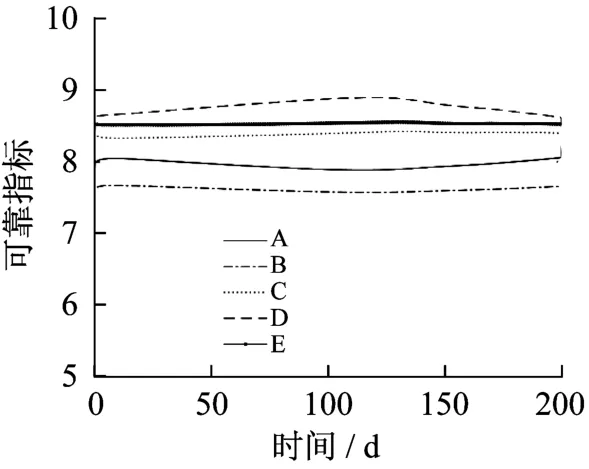
图10 5个截面时变可靠指标的对比分析Fig.10 Comparison analysis of time-variant reliability indices for five sections

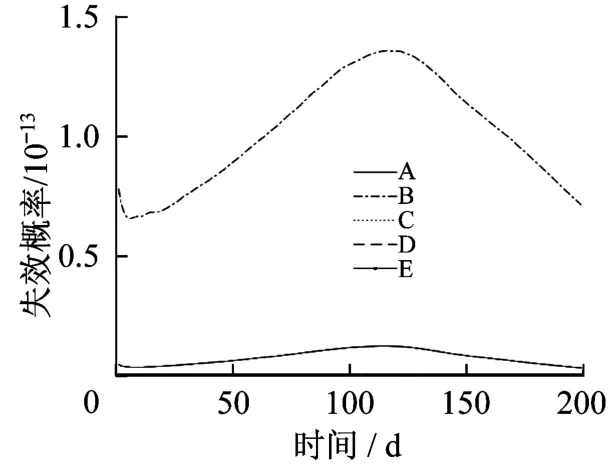
图11 5个截面时变失效概率的对比分析Fig.11 Comparison analysis of time-variant failure probability for five sections

3.3.2 考虑危险监测点失效模式相关性的主梁体系时变可靠性预测

在考虑危险监测点失效模式相关性的条件下对天津富民桥主梁体系的可靠性进行动态预测。基于C藤结构原理，将随机场的5元结构体系分解10个二元串联结构体系，每个二元串联结构体系作为单元模块，分别求出单元模块功能函数之间的时变相关关系，即Copula函数的时变相关系数：ρAB，ρAC，ρAD，ρAE，ρBC|A见图12a 所 示 ；ρBD|A，ρBE|A，ρCD|AB，ρCE|AB，ρDE|ABC见图 12b。其中ρI·J为I与J2 个监测点的时变相关系数；ρI·J|H是以H截面为条件，I与J2个监测点之间的时变相关系数；ρI·J|H·M是以H和M截面为条件，I与J2个监测点之间的时变相关系数；ρI·J|H·M·N是以H、M和N截面为条件I与J2个监测点之间的时变相关系数。

BDVCM的单元模块功能函数为

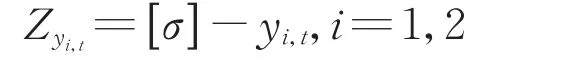
式中[σ]容许应力服从均值为411MPa、变异系数为0.098的正态分布。

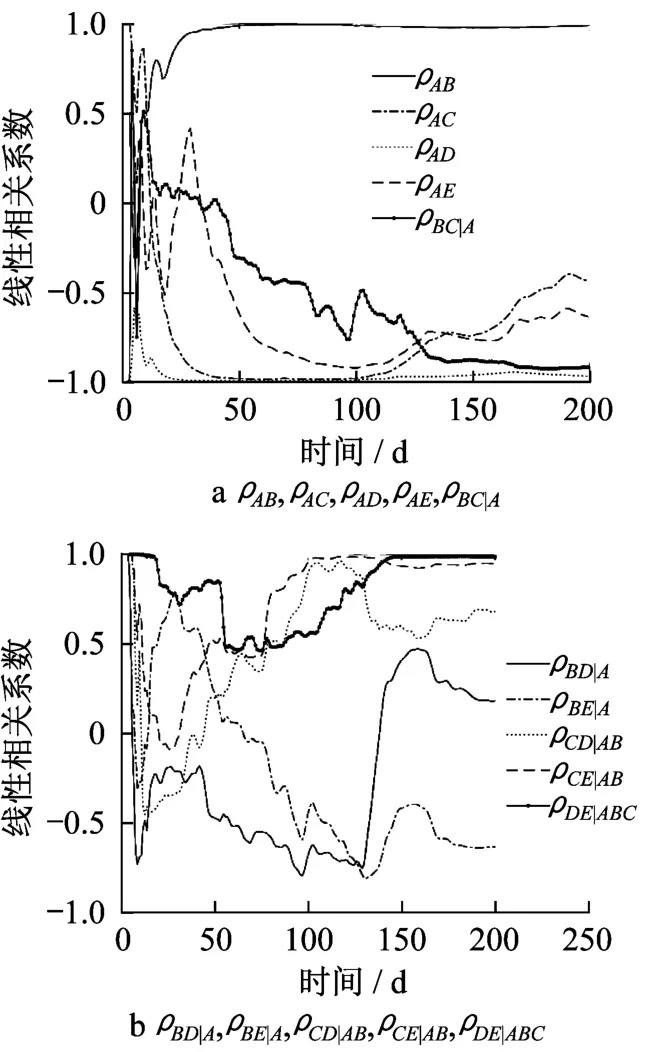
图12 功能函数之间的时变相关系数Fig.12 Time-variant correlation coefficients between performance functions

基于Copula函数的时变相关参数，由Gaussian-Copula函数PDF图和等高线图分析单元模块失效模式之间的时变相关性。以A、E截面为条件，对C、D2个监测点之间的时变相关性进行分析，以第100d的分析结果进行验证，如图13所示。

对5个截面的10个单元模块的时变可靠性预测结果进行对比分析，选取每一天的最大失效概率作为结构体系考虑失效模式相关性的整体失效概率。10个单元模块的失效概率预测结果如图14所示。

选取结构体系考虑失效模式相关性与不考虑失效模式相关性的最大失效概率进行对比分析，结果如图15所示。

由图15可知，随机场考虑失效时变非线性相关性的主梁体系动态预测的失效概率明显低于不考虑失效相关性所计算的结果。因此，不考虑失效相关性所预测的失效概率偏于保守，在主梁体系的可靠性预测分析中，考虑失效模式相关性具有一定的合理性和必要性。

4 结论

图13 时变Vine-Copula函数PDF图和等高线图Fig.13 Time-dependent vine-Copula functions

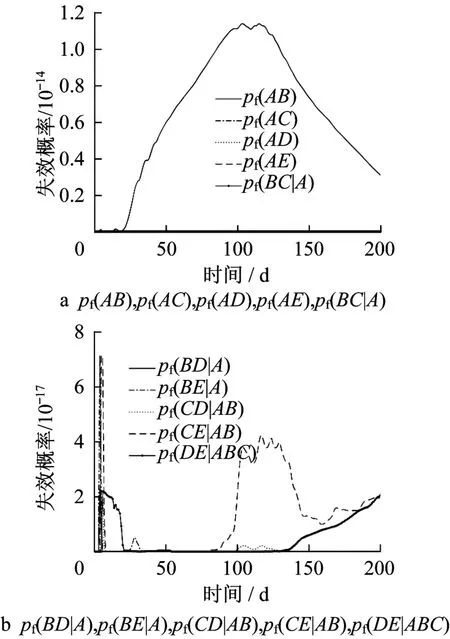
图14 考虑失效模式相关性的5个截面时变失效概率的对比分析Fig.14 Comparison analysis of time-variant failure probability for five sections considering correlation of failure modes

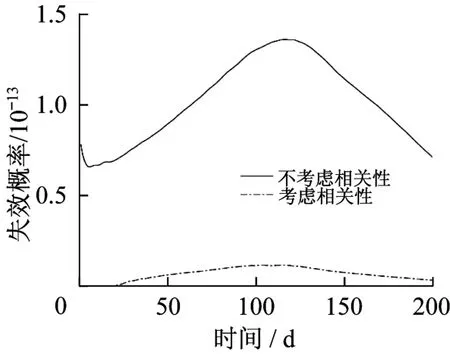
图15 结构体系的时变失效概率Fig.15 Dynamic failure probability of structural systems

在役桥梁主梁截面各个危险点的监测变量形成一个随机场，考虑到各个危险监测点具有相同的随机荷载源，基于危险点的监测数据，融合利用DLM的贝叶斯动态递推过程和藤Copula理论，建立了随机场的BDVCM，并结合FOSM方法，实现了考虑危险监测点失效时变非线性相关性的主梁体系动态可靠性预测。不考虑监测点失效相关性计算所得结果偏于保守，进一步验证了主梁体系动态可靠性分析过程中考虑监测点失效动态非线性相关的必要性。提出的方法适合于在役桥梁历史监测数据较多的情况，且其概率分布可以采用高斯分布近似表示。而对于在役桥梁历史监测数据较少、监测数据服从非高斯分布等情况，需要进一步展开详细研究。因此，为得到更合理的主梁体系可靠性评价标准需要进一步展开研究。