非线性矩阵方程数值解的广义哈密顿算法

段晓敏, 赵新玉, 孙华飞, 纪雪婷

(1. 大连交通大学 理学院，辽宁，大连 116028; 2.大连交通大学 材料科学与工程学院，辽宁，大连 116028; 3.北京理工大学 数学与统计学院，北京 100081)

考虑一类广义非线性矩阵方程

(1)

注意到方程(1)的解是对称正定矩阵, 而对称正定矩阵全体可以构建成一个流形，所以基于流形的几何结构提出求解方程(1)的算法具有很大的优势. 著名的学者Fiori[8]提出了适用于流形上某些问题的广义哈密顿算法(EHA). 这个算法属于渐进二阶收敛的, 比流形上常用的黎曼梯度算法更加高效. 本文基于正定矩阵流形的几何结构, 提出求解方程(1)的EHA算法. 将流形上2个点之间的测地距离作为目标函数，并计算目标函数在流形上的黎曼梯度. 最后通过数值模拟比较EHA算法和经典的MSIM算法的计算行为.

1 预备知识

本节介绍黎曼流形上的几何概念和正定矩阵流形的几何结构[9-10].

1.1 黎曼流形上的几何概念

给定X∈M,V∈TXM, 在黎曼流形M上连接2点的最短线被称之为测地线, 记γX,V:[0,1]→M. 流形上2点之间测地距离定义为测地线的长度l(γX,V). 如果流形上的任意2点之间都有一条测地线连接, 那么就能够测量这个流形上任意2点之间的距离.

(2)

1.2 正定矩阵流形上的几何概念

所有n×n正定对称矩阵可以构成一个流形P(n)，称之为正定矩阵流形. 所有n×n对称矩阵组成的集合为S(n)，那么P(n)的切空间为S(n). 即, 任何一个对称矩阵的指数映射是一个正定矩阵, 反之，任何一个正定矩阵的对数映射都是一个对称矩阵.

定义P(n)上的Frobenius内积

式中：矩阵B1,B2∈P(n)； tr为矩阵的迹. 这个内积赋予P(n)一个平坦的几何结构, 而且测地线退化为直线, 并具有一定的局限性.

改进的Frobenius内积在B处定义为

gB(X,Y)=gI(B-1XB-1Y)=tr(B-1XB-1Y),

(3)

式中X,Y∈S(n). 定义了黎曼度量(3)的P(n)成为一个黎曼流形, 并且使得P(n)是弯曲的. 在B点以X为方向的测地线为

显然这条测地线无条件的被完全包含在P(n)里.P(n)上2点之间的测地距离为

2 广义哈密顿算法

从而方程(1)的精确解X*在目标函数J(X)的最小值点实现

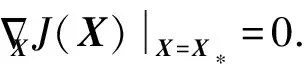
首先需要计算目标函数J(X)的黎曼梯度.

定理1目标函数J(X)在X处的黎曼梯度为

(4)

式中a:=ln(X-1L(X))L(X)-1.

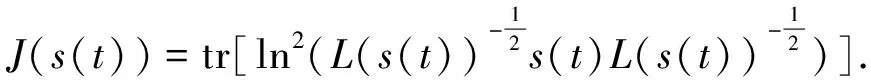
根据式(2)中函数的黎曼梯度的计算方法, 将目标函数J(s(t))对参数t求导得

根据文献[8],P(n)上的广义哈密顿算法为

(5)

式中μ>0为摩擦因数. 将系统(5)离散化可以表示为

(6)

式中η为学习效率. 2个参数η和μ满足

(7)

式中λmax为目标函数J(X)的黑森矩阵的最大特征值. 将式(4)代入式(5), 得到计算方程(1)数值解的广义哈密顿算法(EHA)表示为

离散化之后的EHA算法为

(8)

因此计算方程(1)数值解的EHA算法可以表示为

①X0为输入矩阵X的初始值,V0为是V的初始方向，选取ε>0为容忍系数;

② 计算ρ(L(X)-X)，式中ρ为矩阵的谱半径;

③ 如果ρ(L(X)-X)<ε，算法结束,X为方程(1)的近似解;

④ 通过式(8)更新Xk和Vk，重复步骤②.

3 例 证

举例说明广义哈密顿算法的有效性. 将EHA算法的收敛速度与经典的MSIM算法进行比较. 关于MSIM算法的细节可以参考文献[7]. 模拟中的误差设为ρ(L(X)-X)<10-15.

例1考虑非线性矩阵方程

式中：

在EHA算法和MSIM算法中, 均取Q为初始值X0. 在MSIM算法中将3阶单位矩阵I3作为X1. 在EHA算法中，关于η和μ的选取与算法迭代次数的关系通过图1表示出来. 可以看出EHA算法最少需要19次迭代即可实现事先给定的误差, 这要求0.85<η<0.95,1.05<μ<1.15,并且这2个参数需要满足式(7). 因此η和μ可以取值为图2中的实验数据. 对于事先给定的误差, MSIM算法需要47次迭代, 所以EHA算法比MSIM算法具有更快的收敛速度(见图3).

例2考虑非线性矩阵方程

式中：

Q=I3.

类似于例1的计算过程, 初始值取为X0=Q,X1=2Q,EHA算法和MSIM算法分别需要28次和50次迭代达到事先给定的误差, 其中EHA算法中的参数分别取值为η=0.694,μ=1.328. 所以, EHA算法比MSIM算法具有更快的收敛速度.

4 结 论

基于正定矩阵流形的几何结构, 提出求解一类非线性矩阵方程的广义哈密顿算法. 这个算法具有近2阶的收敛速度. 因为改进的Frobenius内积所诱导的流形是测地完备的, 所以将流形上2个点之间的测地距离作为目标函数. 最后通过2个数值例子表明本文所提出的广义哈密顿算法比经典的多步定常迭代方法收敛速度更快.