圆筒型陶瓷钛合金芳纶三单元层复合靶板结构抗弹性能数值模拟及其内在机理

2020-04-07范群波李鹏茹周豫刘昕

北京理工大学学报 2020年2期

范群波，李鹏茹，周豫，刘昕

(北京理工大学材料学院，北京 100081)

现代战争对轻量化装甲提出了迫切需求，以保证武器装备的高防护性及高机动性. 陶瓷、钛合金与纤维复合材料具有密度低、硬度高、弹塑性强等特点，在轻质装甲结构中广泛应用. 但随着科技进步与反装甲武器的发展，加载环境复杂多变，单个材料组成的靶板结构无法满足目前的防护要求. 由陶瓷、钛合金与纤维复合材料等轻型单元材料组合而成的轻质装甲结构具有质量轻、抗弹性能优良、可设计性强等特点，备受人们的关注.

目前对陶瓷、钛合金与纤维复合材料组合而成的轻质复合靶板结构的研究很多，如Wang等[1]制备了一种由氧化铝陶瓷层、超高分子量聚乙烯(UHMWPE)和两层Ti-6Al-4V(TC4)组成的创新型轻量化复合靶板结构. 研究表明，新型装甲结构重量减轻，且能够抵抗12.7 mm口径穿甲燃烧弹侵彻. Tepeduzu等[2]使用7.62 mm口径穿甲燃烧弹侵彻陶瓷/纤维复合靶板结构，发现在不考虑装甲面密度的情况下，使用氧化铝/S2玻璃/环氧树脂作为背板的复合靶板结构抗弹性能优于背板为氧化铝/芳纶/环氧树脂的复合结构等. Hu等[3]对分块陶瓷与UHMWPE单元层组成的复合靶板结构进行靶试实验，系统研究了分块陶瓷对复合靶板抗弹性能的影响. Li等[4]考察了纤维类型对钛基纤维金属层压板失效的影响，结果表明，在弹道极限和能量吸收方面，Ti/UHMWPE复合层压板结构抗弹性能优于Ti/CFRP(碳纤维增强复合材料)复合层压板结构. Ansari等[5]通过三维有限元模拟研究了玻璃纤维增强复合材料(GFRP)靶板厚度、几何形状和边界条件对靶板结构损伤的影响. Liu等[6]研究Ti6Al4V/UHMWPE/Ti6Al4V组合为背板时的陶瓷复合装甲结构对12.7 mm口径穿甲燃烧弹的作用机理. 研究结果表明，Ti6Al4V作为复合背板中的第三层材料与碳纤维板和铝合金相比，对第一层起到了很强的支撑作用，同时增强了UHMWPE层的能量平衡功能，具有很好的抗弹性能. Nakatani等[7]则研究了轻质装甲Ti/GFRP层压板在低速冲击下的损伤行为，发现GFRP中的分层现象是由于钛层背部的裂纹扩展而引起的.

目前国内外学者对于轻质复合装甲结构抗弹性能的研究已经很多，但相关研究大部分是针对平板，对于异形复合结构的研究比较有限. 然而，具有一定弯曲特征的非平板装甲结构的应用及需求同样广泛，如现代防弹衣等，它要求符合人体工程学，应该被设计为更符合身体曲率的弧形结构. Tan[8]利用ANSYS/Autodyn软件对B4C/Kevlar弧形结构弹靶过程进行了数值模拟，研究了脱黏/分层等预先存在的缺陷对弧形装甲防护性能的影响. Shen等[9]通过实验研究了在爆炸载荷下由两块铝板与中间的泡沫铝芯组成的弯曲夹层板的动态响应过程. 再如头盔异形结构，对于它的研究相对较多. Aare等[10]利用头部有限元模型对头盔刚度、不同的冲击角度等参数作用下头部的生物力学响应进行了仿真研究. Palomar等[11]研究了一种新型的非穿透伤-头盔后部钝伤(BHBT)，建立了由头盔和人头组成的仿真模型，并用文献中的实验数据进行了验证.

从上述文献可以看出，国内外学者针对异形复合靶板结构弹靶作用的研究已经取得了一定的成果. 然而在多单元层异形结构抗弹性能及其内在机理方面的认识仍有不足，需要深入进行研究. 因此，本文选取圆筒型陶瓷-钛合金-芳纶三单元层复合靶板为典型异形结构，使用53式7.62 mm口径穿甲燃烧弹侵彻该复合靶板结构. 通过有限元数值模拟并结合靶试实验验证的方法，研究了圆筒型多单元层复合靶板结构能量的耗散情况以及弹体入射姿态角不同时复合靶板的抗弹性能.

1 构建有限元模型

1.1 有限元几何模型

弹体采用53式7.62 mm口径穿甲燃烧弹，弹芯由T12A合金钢加工而成，头部为尖卵形，直径6 mm，长度27.5 mm. 弹芯的几何模型如图1所示. 仿真过程中弹头的变形行为与其本构模型密切相关，通过失效判据删除单元体现磨蚀现象. 复合靶板形状为圆筒状，为节省运算时间，采用1/2有限元模型，如图2所示. 复合靶板高为93 mm，内径为258 mm，从内到外各单元层依次为芳纶纤维板、Ti-6A1-4V合金板与Al2O3陶瓷板，厚度分别为3，6与6 mm. 陶瓷单元层由弧形陶瓷块拼接而成，陶瓷块的高为31 mm，对应的圆心角为12°. 弹体以760 m/s的速度着靶，使用非线性动力学有限元软件LS-DYNA模拟弹靶作用过程. 模拟过程中采用六面体单元 Solid 164 对其进行网格剖分，整个计算模型共划分为 2 677 753个单元，其中弹体由12 544个单元组成，陶瓷板由2 008 809个单元组成，钛合金板由446 400个单元组成，芳纶板由210 000个单元组成.

1.2 材料模型及相关参数

弹体采用Cowper-Symonds[12]应变率强化模型. 此模型考虑了弹体材料的应变率效应以分析黏塑性对弹体响应的影响，其对本构行为的定量表征如下

(1)

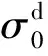
表1 弹体材料的模型参数

陶瓷单元层采用Johnson-Holmquist本构关系[14]. 该模型适用于描述陶瓷、玻璃等脆性物质的失效过程，模型包含了未损伤材料和损伤材料的强度、压力和损伤模型. 归一化强度可以表示为

(2)

未损伤材料的归一化强度可以表示为

(3)

损伤材料的归一化强度可以表示为

(4)

jP*=P/PHEL，

表2 陶瓷材料的模型参数

钛合金单元层的材料模型采用Johnson-Cook本构关系[16]. 该模型用来描述在大变形、高应变率和高温下的材料的强度行为，其描述如下

(5)

钛合金的Johnson-Cook材料模型参数[17]如表3所示. 采用 Gruneisen 状态方程定义 Ti-6Al-4V 钛合金变形过程中压力与体积的关系.

表3 钛合金材料的模型参数

当材料发生压缩时

(6)

式中：P为材料的静水压力；μ=ρ/ρ0-1；S1，S2与S3为vs-vp(冲击波速度-质点速度)曲线斜率的量纲一系数；c为vs-vp曲线的截距；γ0为Gruneisen常数，α为γ0的一阶体积修正项. 钛合金的 Gruneisen 状态方程参数如表 4 所示.

表 4 钛合金的 Gruneisen 状态方程参数

Tab.4 The parameters of Gruneisen state equation for titanium alloy

cS1S2S3γ0α5 1301.0280.00.01.230.17

芳纶板采用正交各向异性弹性材料模型[18](MAT_OPTIONTROPIC_ELASTIC)，该模型适用于弹性模型正交各向异性的实体或薄壳结构，用1，2，3来描述3个坐标轴，各应变分量和应力分量之间的关系可以由式(7)描述为

εm=Cmσm，

(7)

式中：εm=[ε11ε22ε33γ12γ23γ31]T；σm=[σ11σ22σ33τ12τ23τ31]T；Cm为材料的柔度矩阵，

(8)

式中：K11，K22，K33分别为材料在3坐标轴方向上的杨氏模量；G12等参数定义了各方向的剪切模量；ν21等参数定义了各方向的泊松比. 芳纶模型中所用材料参数[19]见表5所示.

表5 芳纶材料的模型参数

2 可靠性验证

图3展示了靶试试验与数值模拟结果中复合板损伤形貌对比图，试验与仿真中弹体初始速度大小均为760 m/s. 根据图3可以看出，陶瓷块开裂破碎，弹体最终撞击在钛合金单元层上形成凹坑，模拟结果与靶试试验结果现象一致. 此外，数值模拟中复合靶板穿深为9.3 mm，试验测得的复合靶板穿深为8.5 mm，相对误差为9.4%. 误差相对较小，表明了模拟计算的可靠性. 误差出现的原因可能为模拟计算中采用理想化各项同性材料模型与实际情况略有差异.

图4为靶试实验与模拟后芳纶板形貌对比图. 由图可见，芳纶板基本无损伤，仅出现小幅度背凸. 经检测可得，试验结果中芳纶背凸高度约为3.2 mm，数值模拟中背凸高度为3.6 mm. 数值模拟与实验结果吻合良好，进一步证明了模拟计算的可靠性.

3 结果与分析

3.1 垂直入射条件下的复合靶板能量分析

弹体侵彻圆筒型复合靶板时动能的耗散涉及多种失效行为：弹头倾斜着靶出现弯折与磨蚀、陶瓷开裂破碎失效、钛合金单元层塑性变形形成弹坑、芳纶板弯曲并出现背凸等等，损伤失效的过程过于复杂. 同时穿深、质量损失、失效区域等效面积等参量无法准确全面地体现复合靶板损伤程度. 因此采用靶板总能统一描述靶板的失效行为，该能量实质为从弹体初始动能中吸收的那部分能量，由靶板的全部单元能量分量求和得到，且包含了在侵彻过程中失效被删除的单元. 定义靶板总能为

ET=ECe-t+ETi-t+EAr-t，

(9)

式中：ET为复合靶板总能；ECe-t为陶瓷单元层总能；ETi-t为钛合金单元层总能；EAr-t为芳纶单元层总能. 各单元层总能用Et表示，又可分为所有现存单元动能Ek总和，所有现存单元内能Ei总和，所有失效单元动能Eek总和，以及所有失效单元内能Ee总和. 因此得到式(10)

Et=Ek+Ei+Eek+Eei.

(10)

根据式(9)(10)，对弹体侵彻复合靶板后的靶板能量进行分析. 图5为弹体垂直入射陶瓷单元层中心区域时复合靶板的能量柱形图，显示了复合靶板的能量耗散情况，由图可知陶瓷板、钛合金板与芳纶板获取的总能分别为1.564，0.257和0.046 kJ.

图6能量分布饼形图显示了各单元层能量占复合靶板总能的比例，其中陶瓷单元层所获取的能量ECe-t占复合靶板总能ET的83.77%，对弹体的能量耗散起着重要作用；钛合金及芳纶单元层耗散的能量百分比分别为13.77%，2.46%. 进一步的计算结果表明，陶瓷单元层失效单元内能Eei与动能Eek分别为0.57和0.56 kJ，明显高于其余各项能量分量. 而钛合金单元层和芳纶单元层的失效单元能量均为0，表明弹体在侵彻复合靶板时，钛合金板与芳纶板没有发生单元失效. 钛合金板与芳纶板组合为背板与陶瓷块紧密贴合，发挥吸能防护作用，具有良好变形能力，使复合靶板能够充分发挥抗弹性能.

3.2 初始入射姿态角对复合靶板结构能量的影响

在本文中，定义靶板的法线方向N指向圆弧内侧，弹体姿态角θ为所在位置圆弧切面对应的法线方向N与弹体轴线之间的夹角，初始时刻弹体速度为760 m/s，入射姿态角为θ0. 由于受力不对称，弹体在侵彻过程中将会发生偏转，侵彻过程中弹体姿态角发生变化. 图7显示了θ0分别为0°，10°，20°，30°，40°，50°，60°，70°时的弹体入射位置. 入射姿态角不同，复合靶板获取的能量也有差异. 分析弹体以不同θ0角度入射时靶板受力、质量损失以及弹靶作用模式的变化特征，从而获得初始时刻入射姿态角θ0对复合靶板能量的影响.

3.2.1陶瓷单元层受力

陶瓷单元层通过外力对其做功获取能量. 在弹体侵彻靶板过程中，靶板受力是波动的，随时间而变化. 以θ0=0°时为例，靶板受力时间历程曲线如图8所示，Fmax表示弹体侵彻过程中陶瓷单元层的受力峰值. 按此方法，提取θ0不同值时的受力峰值，并绘制Fmax随θ0变化的曲线如图9所示. 由图可见，

从0°～70°陶瓷板受力大体上不断减小，并逐渐趋于65 kN附近. 0°时，陶瓷单元层受力峰值Fmax最大，为198 kN；60°时，陶瓷板受力峰值Fmax最小，为62.81 kN. 总体而言，单元层受力越大，获取的能量越多，但弹体侵彻圆筒型靶板时，靶板的能量获取不仅受到外力的作用，还受到弹靶作用模式以及靶板质量损失等因素的影响，将在3.2.2节、3.2.3节详细讨论.

3.2.2弹靶作用模式

根据弹体姿态角的值定义3种弹靶作用模式，如图10所示：模式Ⅰ为弹头冲击靶板结构过程，θ≤85°；模式Ⅱ为弹身冲击靶板结构过程，85°<θ≤95°；模式Ⅲ表示弹尾冲击靶板结构过程，θ>95°.

图11表示了θ0为0°～70°时弹体姿态角θ的变化曲线. 由图可见，θ0为0°～10°时弹体冲击靶板过程仅具有模式Ⅰ，即弹体始终以头部与靶板相互作用. 而20°～70°时，弹体侵彻复合靶板时则具有全部3种模式，表明弹体最初以头部侵彻靶板，随后因偏转导致弹身与靶板相互作用，且最终以弹尾接触靶板形式发生跳弹. 其中，入射角θ0为20°时，弹体偏转最大，姿态角变化为78.50°；θ0为30°时，弹体处于模式Ⅰ的时间明显减少，模式Ⅱ弹身冲击靶板的时间最长，约为76 μs；而40°～60°时，弹尾冲击靶板过程的时间相对较长；θ0为70°时，由于弹体初始时刻入射姿态角接近于模式Ⅱ，弹体接触靶板后就很快进入了弹身与靶板作用阶段，并保持了较长时间,约为56 μs.

3.2.3复合靶板质量损失与能量分析

为揭示陶瓷-钛合金-芳纶三单元层圆筒型复合靶板的抗弹机理，对各单元层吸收能量随θ0的变化进行了研究，计算结果如图12(a)所示. 与3.1节得到的结论类似，弹体以不同姿态角入射时，陶瓷单元层与钛合金、芳纶单元层相比较，其获取的能量始终占复合靶板总能的主导地位. 显然，陶瓷单元层能量决定了复合靶板总能的变化. 能量曲线整体呈逐渐减少的趋势但并非是单调递减.

为进一步分析陶瓷单元层能量变化的原因，揭示质量损失与能量变化的关系，将其与图12(b)陶瓷单元层质量损失曲线进行对比分析，可以发现两者具有很大的相似性：入射角θ0为0°时，陶瓷单元层吸收能量2.22 kJ；0°～10°时，弹体侵彻过程中开始偏转使得陶瓷质量损失增大，陶瓷单元层的能量增多，θ0为10°时，陶瓷单元层能量达到峰值为3.08 kJ；20°时陶瓷单元层质量下降，能量也急剧下降为1.32 kJ；而θ0从40°～70°，陶瓷单元层质量损失不断降低，所吸收的能量也不断降低，70°时陶瓷单元层能量最低为0.47 kJ. 值得注意的是，陶瓷单元层质量损失曲线的变化趋势与能量的变化趋势并不完全相同. 由图可知，θ0为30°时质量损失高于40°而能量却低于40°. 根据3.2.2节的图10讨论可知，30°时弹体大部分的时间处于模式Ⅱ，在此模式下陶瓷单元层大量单元失效，但由于靶板单元在沿着受力方向的移动受到周围单元的限制，因而外力做功较小，获取的能量也少.