非计划再入院风险预测研究

李金林， 赵秀林,2， 张素威， 张增博， 朱镜蓉

(1.北京理工大学 管理与经济学院，北京 100081； 2.联通在线信息科技有限公司，北京 100032；3.南京大学 计算机科学与技术系，江苏，南京 210023)

“健康中国”是我国正在大力实施的一个重要战略. 医疗服务与人民健康紧密相连，关乎全民福祉，一直受到国家的高度重视[1]. 本文针对患者发生非计划再入院的风险预测进行研究.

非计划再入院是指在医疗机构计划外，患者在出院后的一段时间内，如30， 60，90 d等，由于相同或者相关病因发生的再次入院[2]. 非计划再入院会给患者生活带来巨大困扰. 同时，世界各地的医疗机构每年都会因非计划再入院产生大量医疗费用[3-4]，造成医疗资源浪费. 然而，已有的研究表明，大多数非计划再入院是可以通过医疗干预得以缓和甚至避免的[5-6]，包括合适的治疗方案，适当延长住院时间等[2-7]. 目前，再入院率已被多国政府列为评价医疗机构服务质量的一个重要指标. 美国国会将“减少再入院计划”列入医疗法案，而且自该计划启动以来，医疗保险和医疗补助服务中心(CMS)观察到再入院率有明显下降[3]. 我国于2011年出台的《三级综合医院医疗质量管理与控制指标》，共包括7类指标，其中，重返类指标被列为其中的一类[8]. 利用风险预测模型，医疗机构能够根据患者的医疗数据对患者的非计划再入院风险进行提前评估，进而采取合理的干预措施，提升医疗质量，改善患者健康质量，降低非计划再入院率[9].

再入院风险预测的传统模型是以LACE指数和Rothman指数为基础的[10]，这两类指数均是借助实践经验被人工定义的，因此模型的表现取决于经验总结是否准确. 而近年来兴起的基于机器学习的风险预测模型，能够不依赖实践知识从数据中学习出合适的策略，所以基于机器学习的模型往往都能够取得比传统方法更好的预测效果.

针对特定疾病进行的再入院风险预测，其分析对象包括许多常见疾病，如心脑血管类疾病、呼吸道病、流行性感冒以及肿瘤癌症等. Agarwal[11]使用Logistic回归、朴素贝叶斯分类以及高斯核支持向量机，对充血性心力衰竭患者的再入院风险进行预测，发现Logistic回归和朴素贝叶斯分类的预测效果较好. 而Hebert等[12]利用Logistic回归对充血性心力衰竭、急性心肌梗死和肺炎患者的电子病历进行研究，发现Logistic回归对急性心肌梗死和肺炎病例的再入院风险预测表现更好. Yu等[13]则为医疗机构的再入院风险预测提出了一个通用框架，利用心力衰竭、急性心肌梗塞和肺炎患者数据进行实验验证，发现相对于传统的风险预测模型，如LACE模型，该通用框架具有更高的灵活性并且能够取得更好的预测效果. Hempstalk等[14]则基于UCI公开数据库中的糖尿病病人再入院数据集，验证了与现有技术相比，在广泛特征集上使用机器学习方法将提高再入院风险预测的准确性的假设. 在这些已有工作中，由于数据集性质的不同，没有任何一种算法能够胜任全部预测任务，需要根据具体情况选择合适的预测模型.

未针对于特定疾病的风险预测模型同样有许多具有代表性的研究成果. Vaithianathan等[15]基于新西兰医院的公开数据集，根据多元Logistic回归分析患者的社会经济因素和住院指标，建立了风险预测模型，同时得到了影响再入院风险的关键因素包括年龄、性别、最后住院诊断、住院时间和先前住院费用. Futoma等[16]在同一数据集上的研究则表明，随机森林、带有惩罚项的Logistic回归和深度神经网络预测效果较好. 以上研究均通过概率表征再入院风险，而有一些研究工作则通过定义某种特定的指标来表征再入院风险. Donze等[7]基于出院患者的管理数据，使用多元Logistic回归根建立了一种再入院风险评分，并验证了该评分在风险预测中的有效性. Billings等[17]对英格兰的医院统计数据以及英格兰的人口普查数据进行了多变量统计分析，定义了一种表征患者未来12个月内再入院风险的指数，通过调节该指数的分类阈值来表示再入院的发生风险.

总的来说，目前再入院风险预测主要有两种思路：一是直接将对病例分类的概率代替风险值，通过概率来预测患者是否会再入院；二是定义一种新的风险衡量指数，通过对阈值的确定来预测患者是否会再入院. 已有研究将再入院风险预测视作一个二分类问题，即患者在未来一段时间内是否会发生再入院. 如果要同时预测患者发生再入院的时间和风险，则必须修改时间限制，重新建模. 另外，已有研究均是基于国外数据集进行的，其结果对于国内医疗领域的参考价值有限. 因此，本研究立足于国内医疗数据，采用机器学习方法，同时在时间和可能性两个维度上构建非计划再入院风险预测模型，使得预测更全面，实用性更强.

1 数据处理和备选预测模型

本研究所使用的数据来源于我国某区域卫生信息平台. 通过对源数据集进行脱敏、集成规约和转换等预处理，得到研究所用数据集. 基于研究所用数据集，使用神经网络、随机森林和支持向量机3种算法，通过调整模型参数，构建备选风险预测模型.

1.1 数据集介绍

本研究的源数据集包括31张数据表，包括患者信息数据、医疗机构医嘱费用数据、电子病历、住院病案数据、手术明细报告等. 由于医疗数据包含患者大量的个人信息数据，如患者身份证号、姓名和联系方式等，对数据进行了脱敏处理.

经过对研究相关的11张数据表进行数据整合、清理、归约、数据离散化和规范化等预处理后，最终的数据集共有10 262条病例记录，每条记录包含性别、年龄、入院季度、血型等36项患者属性. 其中属于多次非计划再入院的记录有7 168例，占比69.8%，属于单次再入院的记录占比30.2%，有3 094例. 进一步将病例样本按照患者下次入院和上次出院的时间间隔分为4类，并进行重新编码. 住院时间间隔对应的编码及其数量如表1所示.

表1 住院时间间隔对应的编码及其统计信息

Tab.1 Encoding rules and statistics of hospital admission time interval

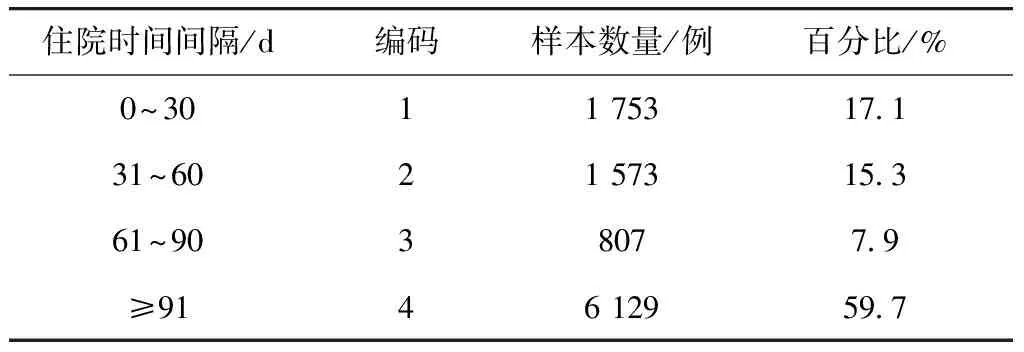
住院时间间隔/d编码样本数量/例百分比/%0～3011 75317.131～6021 57315.361～9038077.9≥9146 12959.7

将入院时间间隔编码作为数据样本的类别标记进行非计划再入院风险预测模型训练和测试.

1.2 基于神经网络算法的模型构建

典型的神经网络包含一个输入层、一个输出层以及一个或多个的隐含层[18]. 本研究采用经典的BP神经网络构建风险预测模型. BP神经网络采用经典的误差逆传播算法，即BP算法，求解神经网络模型参数[19]. BP神经网络求解的主要过程如下.

① 在输入层输入一组数据，即本研究选定的参与预测的属性值.

X={X1,X2,…,Xn},

(1)

② 将输入数据按照网络神经元的连接关系，进行前向传播.

即上一网络层的输出(y)可以作为下一网络层的输入(x). 神经网络中数据由输入层向输出层方向传递的过程称为前向传播. 前向传播的过程可表示为

(2)

式中：hl+1是第l+1层的输出状态向量;h1即为输入层的数据x，wi为该层第i个神经元输入的权重向量. 因此，对于一个m层神经网络，其最终的输出可表示为

(3)

③ 计算输出层输出值与实际值的误差.

假设输出层的实际值为y′，则可以计算输出值与实际值之间的均方误差为

(4)

对应到本研究的预测问题，y′即为输入数据对应的实际风险等级.

④ 按照网络结构将输出层处的误差进行逆传播，并得到参数的更新规则.

BP算法是基于梯度下降策略，以负梯度方向作为参数调整的方向[20]. 考虑到误差是从输出层向输入层的逆向传播，在使用Sigmoid函数作为神经元激活函数时，参数W的更新公式为[21]

(5)

式(5)包含的运算均为向量运算. 其中，m为网络层数，α为训练学习率，λ是权重衰减项. ΔW为权重向量的梯度,

ΔWl=hlδl+1,

(6)

(7)

⑤ 持续迭代直到满足终止条件. 可以设置迭代最大次数，也可以设置梯度的最小变化阈值来结束迭代. 迭代结束时，就得到了最优模型参数，模型训练完成.

神经网络模型的实际应用十分便捷. 在完成网络结构的设计后，将选定的患者数据属性对应地输入到输入层神经元中，并将患者数据对应的风险等级作为预测类别. 训练开始后，算法将自动求解网络中各个神经元处的参数值. 所以，神经网络模型只需人工选定网络结构、输入变量和目标输出，不需要对输入或输出进行额外的设计和处理.

本节中的神经网络风险预测模型的输入变量包括性别、患者年龄、婚姻状况、卡类型、血型、RH、入院季度、出院季度、入院科室编码、疾病大类、实际住院天数、住院时间间隔、医疗付费方式、住院医师数量、累计住院次数、住院病案费用共16项属性. 输出变量为1(0～30 d内)、2(31～60 d内)、3(61～90 d内)、4(91 d以上)，4个风险等级. 因此，神经网络模型的输入层包括16个神经元，输出层包括4个神经元. 通过设置不同的神经网络隐含层的层数和神经元数，可以得到不同的神经网络模型.

为了得到基于本研究数据集预测效果最好的神经网络模型，首先对神经网络隐含层的神经元数进行一定的调整，获得不同的网络结构，然后从中选取预测效果相对较好的网络结构作为本节的风险预测模型. 在此对网络结构的详细信息进行列举，如表2所示. 本次列举了3种网络结构，包括2层隐含层-每层10个神经元的结构、2层隐含层-每层20个神经元的结构和2层隐含层-每层30个神经元的结构. 以上网络结构仅在隐含层数和神经元数进行了调整，保留了相同的输入、输出层，且在各层神经元间采用了全连接.

表2 神经网络模型详细信息Tab.2 Details of neural network models

1.3 基于随机森林算法的模型构建

随机森林(random forest，RF)是一种集成学习模型. 集成学习模型是指将多个基学习模型通过某种策略结合起来，作为一个整体来训练和使用. 随机森林的基学习模型是决策树模型. 决策树模型能够从样本数据中学得一个树形结构[21]. 树的叶子结点表示最终决策，即输入数据的预测类别，对应样本的非计划再入院风险等级. 树的根结点和中间结点都具有判断和划分功能，能够根据结点处的条件将流经结点的数据划分出子集并向后传递，这些结点也和离散化处理后的属性建立了对应关系. 决策树在工作时，从根节点开始根据每个节点处划分属性的取值对当前数据进行划分，每个取值对应一个数据子集. 为保证树结构每增加一层都对决策树建立有利，需要从数据的所有属性中选择最合适的划分属性，即能最大限度降低数据集混乱度的属性. 为此，定义了信息增益、信息增益率、基尼指数等衡量标准. 选定节点划分属性的过程，就是决策树建立的过程. 所以决策树模型学习的关键在于找到符合要求的划分条件，包括根据什么属性划分和如何划分[22].

在决策树模型的发展过程中，研究者提出了多种决策树模型. 如ID3、C4.5、CART、CHAID和QUEST等. 这些模型的思路与基本模型大致相同，通常只是在最优划分属性选择的标准上做了改动. 如ID3使用信息增益；C4.5使用信息增益率；CART使用基尼指数；CHAID和QUEST算法则采用卡方检验选择最优属性. 这些衍生模型各有千秋，其擅长数据集的特征各异. 在使用时应根据数据集的实际情况选择合适的衍生模型.

随机森林是将多个决策树模型集成起来，共同训练和使用. 随机森林模型就是基于Bagging[23]策略的集成学习模型. Bagging方法则是将多个学习器并行训练. 对同一个样本数据集重复采样多次，得到多个采样集，然后在各个采样集上分别训练一个决策树模型，最后将每个学习器对测试样本的预测结果汇总. 另一种集成策略是Boosting[24]方法.

本节的随机森林风险预测模型的输入变量包括入院季度、出院季度、入院科室编码、疾病大类、实际住院天数、住院时间间隔、住院医师数量、累计住院次数、住院病案费用共9个变量. 输出变量为1、2、3、4等4个风险等级. 由于在构造随机森林模型的过程中需要不断选择中间判断结点，因此，为模型输入太多变量可能会干扰模型的训练，不利于最后的预测. 此外，由于决策树深度的限制，模型大部分的输入变量并没有机会被用于最终预测. 所以，与其他预测模型相比，随机森林模型的输入变量相对较少.

随机森林模型的区别主要在于构成森林的决策树类型以及决策树的数量. 在此对随机森林模型的详细信息进行展示，如表3所示. 决策树共采用了CART和CHAID两类，模型的决策树数量有10、20、40棵三类.

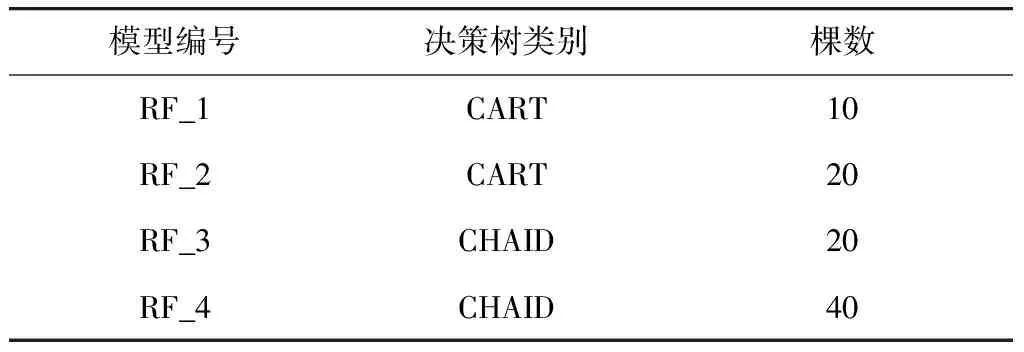
表3 随机森林模型详细信息Tab.3 Details of random forest models

1.4 基于支持向量机算法的模型构建

支持向量机(support vector machine，SVM)是Vapnik等[25]于1995年首次提出的，模型的基本思想是从数据中学习得出一个能将样本空间划分为若干部分的超平面. 在本文的研究场景中，所有的样本属性构成一个高维样本空间，假设需要寻找的划分超平面可以用一个线性方程表示为

wTx+b=0，

(8)

在超平面两侧分别假设一个“支持向量”，使得

(9)

两支持向量与超平面的距离之和为

γ=2/‖w‖.

(10)

γ称为支持向量的间隔. 间隔越大，说明超平面的分类效果越好. 所以，从间隔入手就可以建立一个优化模型，该模型可以用拉格朗日乘子法和SMO算法配合求解[26]. 原始的支持向量机模型仅能解决二分类任务，而本研究中的风险等级共有4种，故需要对支持向量机进行多分类的拓展. 支持向量机的多分类拓展主要有两种思路[27]：“一对多”和“一对一”.

以本研究应用场景为例. “一对多”思路是指选定一种类别作为正例，其余类别作为反例，按照这种划分方式进行多次训练. 如将风险等级为1的样本作为类别正例，风险等级为2、3、4的作为反例，训练得到一个支持向量机模型. 依次选择不同的类别作为正例，分别训练可以得到4个支持向量机模型. 取4个模型计算值中的最大值作为测试样本的预测结果. “一对一”思路则是将4种类别的数据样本进行两两组合作为正反例训练，可以得到6个支持向量机模型，测试样本的预测结果由6个支持向量机模型采用投票法决定. 本研究中采用“一对多”策略构建的多分类支持向量机模型.

上述方法与推导都建立在样本空间线性可分的的前提下，即存在一个超平面能够将样本空间划分开来. 若样本空间线性不可分，考虑将原样本空间投影到更高维空间中去，然后在高维空间中寻找超平面. 在投影过程中需要大规模计算，利用核方法[21]可以降低计算量.

核方法使用的将原有样本空间投影到更高维空间的函数称为核函数[28]. 常用的核函数有线性核函数、多项式核函数、高斯核函数和Sigmoid核函数等. 这些核函数有各自对应适用的样本空间类型. 核函数的选择已经成为影响支持向量机模型性能的最重要的因素之一，因为在实际应用中，简单的线性可分的样本空间几乎不存在. 采用不同的核函数就得到不同的支持向量机模型.

采用核方法的支持向量机模型善于解决非线性问题，尤其是高维非线性问题. 本研究涉及的数据集维度较高，适合采用带核方法的支持向量机模型进行处理. 本节支持向量机风险预测模型的输入变量包括性别、患者年龄、婚姻状况、卡类型、血型、RH、入院季度、出院季度、入院科室编码、疾病大类、实际住院天数、住院时间间隔、医疗付费方式、住院医师数量、累计住院次数、住院病案费用共16项属性. 输出变量为1～4等4个风险等级. 使用常用的高斯核(RBF)、多项式核(PK)以及线性核(LK)分别构造支持向量机模型，进而从中选取预测效果相对较好的支持向量机模型. 以上模型仅在核函数上有区分，其余设置相同.

2 风险预测模型选择

基于上一节构建的3大类10个预测模型，比较各模型在数据集上的预测性能以得到同一算法中预测结果相对较好的备选风险预测模型. 最后，比较3种备选风险预测模型的综合性能，决定本研究最终采用的非计划再入院风险预测模型. 对于所有实验，随机选择80%的数据集作为训练集，用于训练预测模型. 其余20%作为测试集，用于对模型性能评估. 主要评估指标是模型预测准确率.

2.1 基于神经网络算法的预测模型选择

在2.1中，调节神经网络隐含层的神经元个数构建了3个备选模型，分别为2层隐含层-每层10个神经元 (NN_10_10)、2层隐含层-每层20个神经元 (NN_20_20)及2层隐含层-每层30个神经元(NN_30_30). 统计3种模型在测试集上的预测准确率如表4所示.

表4 基于神经网络的模型预测准确率统计

Tab.4 Statistics of prediction accuracy of neural network-based models

由表中不难看出，N_30_30模型，即包含2层隐含层、每层有30个结点的神经网络模型的总体预测准确率最高，且其在4个子类别的预测准确率也均高于其他3个神经网络模型，分别为89.22%、89.32%、81.78%和98.01%. 就总体预测准确率和子类别准确率而言，N_30_30模型预测效果最好.

从表中分析得知，随着网络结构隐含层结点数量的增加，即随着网络结构复杂度的不断提升，模型的预测效果越好. 而这种性能的提升是以快速增长的训练时间开销为代价的. 因此，依据数据挖掘中选用算法的标准，综合考虑模型的预测精确度和增加网络结构复杂度花费的成本与收益，在此选择包含2层隐含层且每层有30个结点的神经网络模型作为备选风险预测模型进入下一阶段的遴选.

2.2 基于随机森林算法的预测模型选择

基于随机森林算法的备选模型共有4个：10棵CART树构成的模型(RF_1)，20棵CART树构成的模型(RF_2)，20棵CHAID树构成的模型(RF_3)，40棵CHAID树构成的模型(RF_4). 统计各模型在测试集上的预测准确率见表5.

表5 基于随机森林的模型预测准确率统计

Tab.5 Statistics of prediction accuracy of random forest-based models

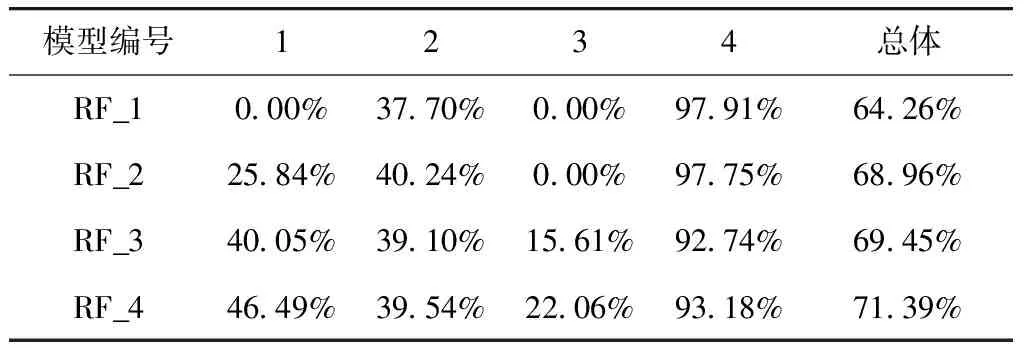
模型编号1234总体RF_10.00%37.70%0.00%97.91%64.26%RF_225.84%40.24%0.00%97.75%68.96%RF_340.05%39.10%15.61%92.74%69.45%RF_446.49%39.54%22.06%93.18%71.39%

由表中信息可知，4种随机森林模型的总体预测准确率分别为64.26%(RF_1)、68.96%(RF_2)、69.45%(RF_3)、71.39%(RF_4). 其中，RF_4模型，即由40棵CHAID决策树组成的随机森林模型的总体预测准确率最高，且其在4个子类别的预测准确率也均高于其他3个随机森林模型，分别为46.49%、39.54%、22.06%和93.18%. 就总体预测准确率和子类别准确率而言，RF_4模型预测效果最好.

从表中分析得知，在决策树类别相同的前提下，模型的预测结果随着决策树数量的增加而提升. 此外，对于本研究所用数据集，CART决策树的预测效果略逊于CHAID决策树，即对于本研究所用数据集而言，更适合采用CHAID决策树进行分类预测.

因此，综合考虑模型的总体预测精确度和子类别预测精确度，在此选择由40棵CHAID决策树组成的随机森林模型作为备选风险预测模型进入下一阶段的遴选.

2.3 基于支持向量机算法的预测模型选择

在2.3中，调节支持向量机算法所采用的的核函数类型，构造了3个基于支持向量机的预测模型，分别为使用高斯核函数的模型(SVM_RBF)、使用多项式核函数的模型(SVM_Poly)、使用线性核函数的模型(SVM_LK). 统计各模型在测试集上的预测准确率见表6.

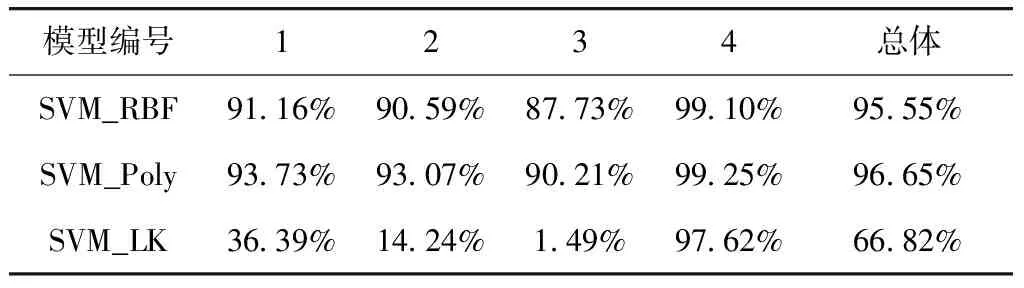
表6 基于支持向量机的模型预测准确率统计Tab.6 Statistics of prediction accuracy of SVM-based models

由表中信息可知，3种随机森林模型的总体预测准确率分别为95.55%(高斯核)、96.65%(多项式核)和66.82%(线性核). 其中，使用多项式核函数的支持向量机模型的总体预测准确率最高，且其在4个子类别的预测准确率也均高于其他两个支持向量机模型，分别为93.73%、93.07%、90.21%和99.25%. 就总体预测准确率和子类别准确率而言，使用多项式核函数的支持向量机模型的预测效果最好.

从表中分析得知，在3个支持向量机模型中，使用线性核函数的模型预测效果最差，可能是由于使用线性核函数的支持向量机模型不适合处理属性均为离散型的数据集. 综合考虑模型的总体预测准确率和子类别预测准确率，在此选择使用多项式核函数的支持向量机模型作为备选风险预测模型，进入下一阶段的遴选.

2.4 最终预测模型的选择

在前述比较过程中，选取了包含2层隐含层且每层有30个结点的神经网络模型、由40棵CHAID决策树组成的随机森林模型和基于多项式核函数的支持向量机模型分别作为神经网络、随机森林和支持向量机在本研究所用数据集上的非计划再入院风险预测模型. 下面将进一步比较各模型的综合性能.

使用查准率P(precision)和查全率R(recall)来综合评价各模型的预测精度. 两指标的计算依赖于混淆矩阵. 混淆矩阵是用来综合评价分类预测模型性能的一种辅助矩阵[21]，其元素见表7. 表中的PT为被正确分类的样本数，NF为原本属于某一类却被预测为其他类的样本数，PF为原本属于其他类却被预测为某一类的样本数，NT则为原本属于其他类且被预测为其他类的样本数[21].

表7 分类结果混淆矩阵Tab.7 Confusion matrix of classification result

P指标和R指标的计算方法为

(11)

(12)

另外，混淆矩阵面向的是二分类问题. 而对于多分类问题，可以将其视为由多个二分类问题组成[21]. 如本章所述的分类问题，可以将其视为由4个二分类问题组成根据混淆矩阵的定义，统计3个模型预测结果的混淆矩阵元素，如表8所示. 根据表中内容，依据查准率和查全率的计算公式，对3个模型的P指标和R指标进行计算，得到的结果见表9.

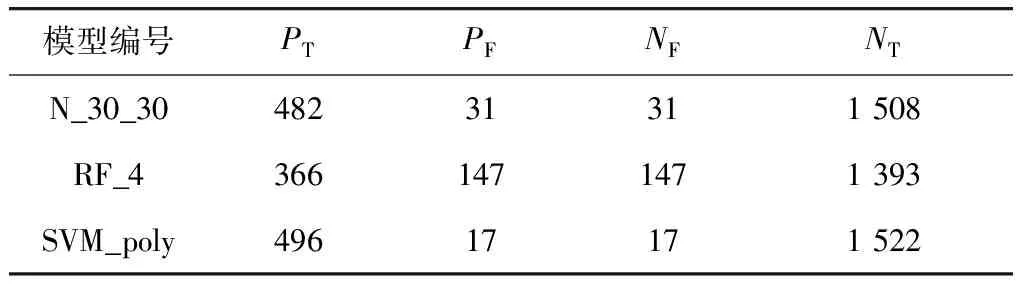
表8 模型预测结果混淆矩阵元素Tab.8 Confusion matrix elements of models’ prediction

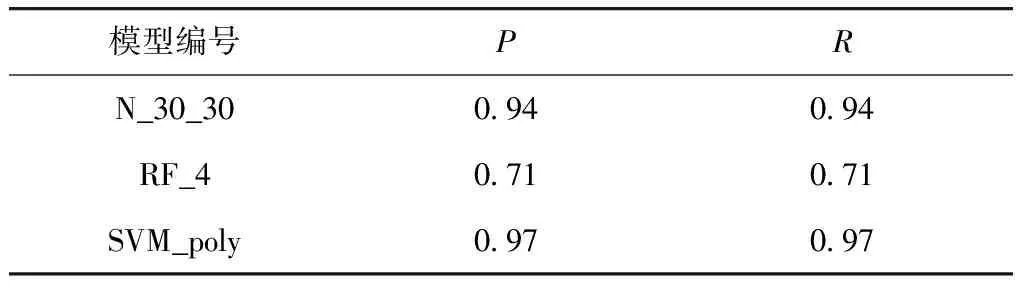
表9 模型预测结果的查全率和查准率Tab.9 Recall and precision of models’ prediction

由于模型的PF和NF值相同，因此模型计算得到的P指标值和R指标值相等. 且由表可知，对于P指标值和R指标值，SVM_poly模型的最高，N_30_30模型的次之，RF_4模型的最低. 对于预测模型而言，P指标值和R指标值越高，代表其预测性能越好. 故SVM_poly，即使用多项式核函数的支持向量机模型，是3个模型中预测效果相对最好的模型，也是本研究多个预测模型中，预测效果最好的模型，因此，选其作为本研究最终的非计划再入院风险预测模型.

在得到非计划再入院风险预测模型后，就可以在更大的数据集上训练出新的使用多项式核函数的支持向量机模型. 训练数据集越大意味着模型代表性越强，模型预测结果的可信度越高. 模型输入为包含性别、患者年龄、婚姻状况、卡类型、血型、RH、入院季度、出院季度、入院科室编码、疾病大类、实际住院天数、住院时间间隔、医疗付费方式、住院医师数量、累计住院次数、住院病案费用等16项属性的数据，输出为预测风险等级. 院方可以根据预测的风险等级对高风险病人进行识别，并对其采取针对性干扰措施，以降低患者非计划再入院的风险.

3 结束语

基于我国某区域卫生信息平台的医疗数据，对非计划再入院风险预测问题进行深入研究. 针对已有工作中将非计划再入院风险预测问题作为二分类问题处理的不足，本文提出了多分类预测的方法，在非计划再入院的时间和可能性两个维度上进行预测. 在研究方法上，选取了神经网络、随机森林和支持向量机3种机器学习算法，通过修改参数设置，构建了10种非计划再入院风险预测模型. 经过对预测结果的综合分析，确定了本研究最终采用的风险预测模型——使用多项式核函数的支持向量机模型. 该模型在测试数据集上达到了96.65%的预测准确率以及相对最高的查全率和查准率. 且该模型具有良好的泛化能力，能够在相同应用场景下的不同数据集上训练并进行预测，其预测结果能够为医疗机构的决策提供有力支持.