轻敲模式原子力显微镜相位、频移特性研究

刘运鸿，郑骁挺，魏 征

(北京化工大学机电工程学院，北京 100029)

原子力显微镜(atomic force microscope，AFM)的核心部件是一种力传感器——微悬臂梁。在工作过程中，探针-样品间的相互作用力使得微悬臂梁的挠度、振幅、相位等力学量发生改变，这些改变反映的是样品的物理、化学特性。如何从原子力显微镜的像图(如高度像、相位像等)解读样品特性，一直是理论工作者和实验工作者非常关注的方向[1]。

振幅调制原子力显微镜(amplitude modulation AFM，AM-AFM)为研究样品表面的物质构成、黏弹性、摩擦特性和黏附特性提供了强大的表征方式。AFM相位成像是AM-AFM的一个附加功能，其通过记录探针振动与激励信号之间的相位差进行成像，需要在扫描图像前确定驱动AFM探针的激振频率，此频率一般选在探针微悬臂梁一阶固有频率附近。目前国内外学者针对AFM激振频率进行了深入研究：黄强先等[2]发现悬臂梁在其一阶频率振动时会对样品的特性更加敏感，而随着悬臂梁从一阶往更高阶过渡，这种敏感性会下降；谢宇辰等[3]发现当激振频率高于共振频率时，引力域成像效果明显提升；谢洪勇等[4]发现合适的针尖平衡位置与样品表面距离可使微悬臂共振频率发生剧烈变化；丁文璇等[5]通过建立微悬臂的振动模型，证明在轻敲模式下采用较小的激振频率可以减小微悬臂自由端振动偏转角,进而减小测量误差。文献[6]～[8]对不同微生物或生物细胞的最佳成像条件进行分析，从而找到适合于此类样品的最佳扫描频率。在实际的AFM操作中，通常将悬臂梁自由振动时振幅为最大振幅95%处所对应的频率选为激振频率。

本文基于微悬臂梁的相频特性曲线中激振频率与相位之间的关系，发现激振频率的选取对相位像分辨率会产生较大影响，且激振频率小于系统一阶固有频率时，能得到对比度较大的相位像。

1 位移激励的支承运动模型

在AFM的实际应用中，可以将悬臂梁的振动看作是位移激励施加在悬臂梁的端部，系统受到位移激励从而进行的强迫振动；Cleveland等[9]认为，使用轻敲模式进行形貌扫描的过程中，相位像与探针-样品间相互作用的能量耗散有关。魏征、陈少勇等[10-11]将轻敲模式下原子力显微镜系统看成是由单自由度的质量、弹簧、阻尼组成的系统，建立了AFM悬臂梁的简化模型，对AFM的振动进行了计算分析。为分析激振频率对相位的影响，结合众多学者的研究成果及振动力学知识，本文采用支承运动模型，如图1所示。图中悬臂梁根部为激励端，压电管受正弦激励电压后在根部施加了一个大小为y(t)的位移激励(为了方便，下文简写为y)，探针尖端与样品间歇式接触，将影响悬臂梁的响应，其动力学参数如振幅、相位直接反映样品信息。模型采用Euler-Bernoulli梁，其动力学方程为偏微分方程，加上激励和约束条件，求解较为复杂。位移激励为正弦模式，频率为单频，依据振动理论，响应频率等于激振频率,因此可以将振动模型简化为一维弹簧振子模型，如图2所示。

图1 原子力显微镜激励响应示意图

图2 原子力显微镜探针-样品振动系统简化模型

在图2所示模型中，支承端正弦运动依然为y：

y=asin(ωt)

(1)

式中：a为支承振动振幅；ω为激励频率；t为时间。

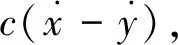
(2)

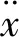
(3)

求解式(3)可得稳态解：

(4)

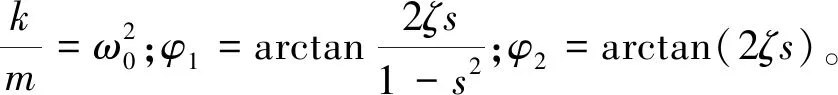
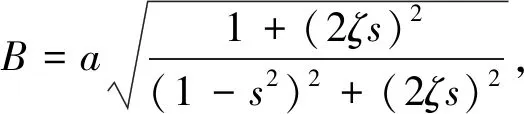
(5)

则式(4)可以化简为：

x=Bsin(ωt-φ)

(6)

令振幅放大因子为β，则：

(7)

2 激振频率对相位像分辨率的影响

如图1所示，微悬臂梁的振动可看作是一种由位移激励所引起的受迫振动，位移激励作用在固定端。引入实验中常用表征能量耗散的参数品质因子Q，Q反比于相对阻尼系数，即Q=1/(2ζ)，且不同样品由于其物理化学特性不同，对应不同的Q值。将式(5)和(7)进行改写，得到以品质因子和频率比表示的幅频函数：

(8)

以及相频函数：

(9)

通过式(8)可得不同品质因子下相位与频率比之间的关系曲线,即相频函数的关系曲线,如图3所示，图中按箭头所指方向品质因子依次为500，200，100，50，20，10，5，2，1，0.5。

图3 相频函数的关系曲线

在实验环境中，微悬臂梁品质因子的范围一般为200～500，为了能够找到与实验情况相匹配的激振频率，本文又对品质因子分别为200，300，400，500时的情况作振动系统的幅频曲线，如图4所示。图中从下往上的曲线其品质因子依次为200，300，400，500。

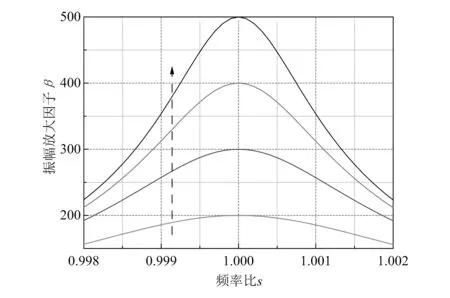
图4 不同品质因子下相对振幅β与频率比s的关系曲线

当压电管的激振频率等于微悬臂梁一阶振动的有阻尼固有频率时，微悬臂梁自由端的振幅达到最大。但是从相位角度看，当压电管的激振频率与固有频率相等时，微悬臂梁的相位偏移量相对于样品表面形状变化灵敏度几乎为零。在图5中可以看到，当压电管的激振频率从微悬臂梁一阶振动固有频率的100%处下降到99.5%处的过程中，在相同激振频率下不同品质因子对应的相位从90°附近下降到20°附近。在这一过程中，可以发现不同曲线之间的间距由小增大再减小，说明相位敏感度由不敏感到敏感再到不敏感。图中按箭头所指方向品质因子依次为200，250，300，350，400，450，500。

图5 支承运动相频曲线

根据图4可知，频率过小会使悬臂梁的振幅变小，使得其对形貌测量不敏感，因此将分析的频率比选在99.8%以上。为了对比同频率比下不同品质因子的相位差，将品质因子为200和50时的相频曲线作为参考曲线，并与其余曲线做差值，如图6所示。图6(a)为同频率比下不同品质因子与品质因子为200时的相位差值曲线,按箭头所指方向做差曲线依次为 500-200，450-200，400-200，350-200，300-200，250-200；图6(b)为同频率比下不同品质因子与品质因子为50时的相位差值曲线，按箭头所指方向做差曲线依次为350-50，300-50，250-50，200-50，150-50，100-50。

图6 支承运动同频率比下不同品质因子的相位差值曲线

从图6(a)可以很清楚地看出，随着压电管的激振频率从微悬臂梁一阶振动有阻尼固有频率的99.8%增加到100%，微悬臂梁响应信号的相位差呈现出先增大后减小的趋势，并在频率比为100%时最小。由此证明，当压电管的激振频率等于微悬臂梁的一阶振动有阻尼固有频率时，即使振动系统的品质因子发生了改变，也无法从相位图上得到具体信息，而且激振频率选取在一定频率比区间内可以使相位像的分辨率达到最大值。从图6(b)可知，依然存在一个频率比区间对相位像的分辨率很敏感。

在相位扫描实验中有一个有趣的现象，不同的操作者对同一样品进行扫描时，可能会获得差别较大的相位图。图3和图5能定性地解释这个现象，即由于不同操作者选取激振频率的差异，使得相位分布于不同的相位区间内。这说明要想获得高品质的相位图，则要根据不同类型的悬臂梁选定合适的激振频率。

3 结束语

本文基于振动理论，通过将探针-样品振动系统简化为一维振子模型，分析了AM-AFM的激振频率对相位的影响，发现相位分辨率会随着激振频率逐渐接近微悬臂梁的一阶固有频率，并呈现先增大后减小的趋势，因此激振频率存在一个较优区间，在此区间内，相位灵敏度最大，这对获得高分辨率的相位像有一定的借鉴意义。同时，本文建立的振动模型也解释了不同操作者所得相位图存在差异的原因。