基于目标约束函数的汽车电子机械制动系统性能优化

文定凤，范先龙

(贵州省电子信息高级技工学校，贵州 都匀 558000)

随着我国经济的快速发展，汽车数量急剧增多，汽车行驶安全问题频发，主要原因是汽车电子机械制动系统(以下简称制动系统)安全性能较差。汽车行驶过程中，制动系统受到制动器、轮胎以及车辆旋转等外力作用形成缝隙，该缝隙降低了汽车制动力，使驾驶人员行车危险性增加。制动系统的主要部件是制动泵，当制动泵出现问题时，制动系统摩擦力变小导致制动力降低[1]。制动系统中制动泵出现故障阻碍汽车回油，使汽车在行驶过程中遇见危险无法及时作出反应，从而降低了行车安全性。为避免制动系统出现故障，在汽车电子机械制动系统中设置制动助力器，以提升汽车行驶过程中的安全性[2]，制动助力器可以使汽车车轮抱死时的制动减速度减小。针对汽车制动过程中可能出现的危险，本文提出基于目标约束函数的汽车电子机械制动系统性能优化方法，可有效提升制动系统的制动性能。

1 制动系统性能优化

1.1 制动系统组成

制动系统主要包括电机、转换装置、减速器等，系统运行结构图如图1所示。

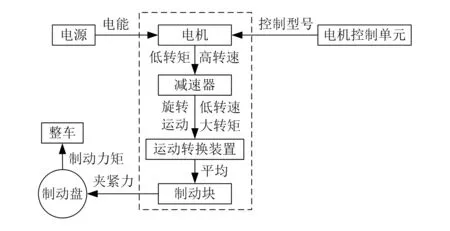
图1 汽车电子机械制动系统运行结构图

在制动系统中，电机通过减速器使输出转矩增加，利用运动转换装置实现汽车转向、直行等运动方式的转换，通过制动块以及制动盘实现汽车减速动作，通过电机控制单元实现汽车制动控制操作[3]。

1.2 目标约束函数

1.2.1基于目标函数的汽车不同载荷使用率分析

汽车行驶过程中，通过分配制动力实现汽车制动，因此制动系统性能优化问题即为制动力分配优化问题[4]。依据汽车前后轴制动力分配情况可知，为避免汽车因后轮抱死导致侧滑引起汽车失控[5]，制动器前后轴制动力分配曲线应位于理想前后轴制动器制动力分配曲线下侧。当汽车制动时，若前轮出现抱死将导致汽车无法控制转向[6]，因此要避免出现前轮抱死情况。当前后轴制动力分配曲线与理想前后轴制动器制动力分配曲线距离最短时，能够增加前轮附着效率[7]，当前后轴制动力分配曲线处于直线y=x上方时，制动力分配为最优。通过以上分析建立制动系统性能优化目标函数如下：

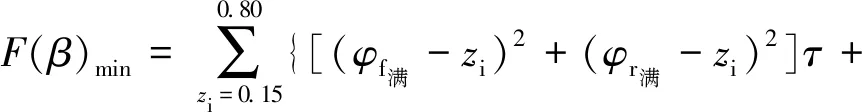
(1)

式中：φf满与φf空分别为前轮满载时与前轮空载时的附着系数；φr满与φr空分别为后轮满载时与后轮空载时的附着系数；zi为制动强度；τ为满载率；F(β)min为汽车满载与空载时前后轴实际附着系数和理想前后轴制动器制动力分配曲线差值。

通过式(1)可知，汽车制动力分配问题为非线性优化问题。汽车制动强度在0.01～0.80，以0.01为单位选取，依据F(β)min的平方和建立目标函数，建立目标函数的过程中应考虑汽车在满载情况以及空载情况下的使用率问题。

1.2.2基于约束函数的系统制动力最优分配

制动系统性能优化最终目的是使汽车在制动过程中前后轮不在相同时间抱死[8]，且后轮抱死时的制动减速度应小于前轮。以N1类汽车为例优化电子机械制动系统性能，N1类车型是指最大设计总质量不超过3 500 kg的载货车辆。

1958年联合国欧洲经济委员会颁布了联合国欧洲经济委员会汽车法规(简称ECE)，ECE法规是推荐性法规，不是强制性标准。ECE法规代号R13H下的法规是乘用车制动系统型式认证的统一规定[9]。

N1类汽车ECE相关法规R13H规定：

1)汽车制动强度为0.01～0.30时，汽车前后轴的利用附着系数φ应满足zi-0.08≤φ≤zi+0.08，由此可得制动系统性能优化约束函数c(1)～c(8)：

(2)

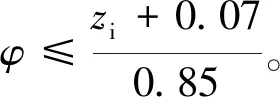
(3)

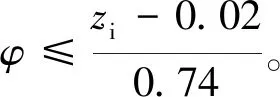
(4)

4)无论何时汽车前轴的利用附着系数曲线均应位于后轴附着系数曲线下方。由此可得制动系统性能优化约束函数c(15)和c(16)：

(5)

5)汽车整车最小附着效率Emin应满足Emin≥75%。由此可得制动系统性能优化约束函数c(17)～c(20)：

(6)

依据以上约束函数求解式(1)的目标函数，可获得汽车电子机械制动系统制动力最优分配结果。

1.3 汽车电子机械制动系统性能优化

制动系统中制动压力大小主要受制动阀平衡力影响，制动力分配由制动阀水平及竖直方向的振动响应所决定，因此系统制动力最优分配问题可转化为系统的制动压力响应优化问题。

设制动系统中制动阀所受水平、竖直方向的制动激振力分别为Fex，Fey，激振力矩为Me，在Fex，Fey，Me作用下的机身水平及竖直方向的振动响应分别为Δ1x，Δ2x，Δ3x以及Δ1y，Δ2y，Δ3y。由此得到制动系统中制动阀在水平及竖直方向上的振动响应Δx，Δy：

(7)

基于制动系统性能优化目标函数以及约束函数建立汽车制动力综合平衡优化模型K如下：

K=γxΔx+γyΔy

(8)

式中：γx，γy分别为制动阀受水平、竖直方向振动响应的加权系数。

将制动系统中制动阀受单位简谐激振作用所引起水平及竖直方向动态响应与制动阀受水平激振力引起的阶分量振幅相结合[10]，获取制动阀受激振力影响造成水平方向以及竖直方向振动响应。

水平制动激振力振动响应求解过程如下：制动系统作用时，简谐载荷cos(nωt)为第n阶水平方向所受载荷，设由简谐载荷造成制动阀水平、竖直方向的振动响应为σ1nx,σ1ny，可得第n阶水平方向制动阀受单位简谐激振作用所引起水平以及竖直方向动态响应σ1x与σ1y：

(9)

通过式(9)可知，在简谐激振力的作用下，制动阀水平方向与竖直方向动态响应由制动系统结构所决定。

制动阀受水平激振力Fex引起的n阶分量振幅vex公式如下：

(10)

式中：axn，bxn分别为不同阶数下水平、竖直方向上的振幅。

制动阀在制动系统工作过程中因振动引起的变形较小[11]，因此其动态响应近似线性，将式(9)与式(10)合并获取制动阀受水平制动激振力Fex影响造成水平方向以及竖直方向振动响应Δ1x及Δ1y：

(11)

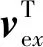
2 实验测试

在Visual C++平台中，利用汽车制动性能评价系统评价采用本文方法优化的汽车制动系统性能，选取BJ1061汽车作为实验对象。

将整车参数输入汽车制动性能评价系统中，系统参数输入界面如图2所示。

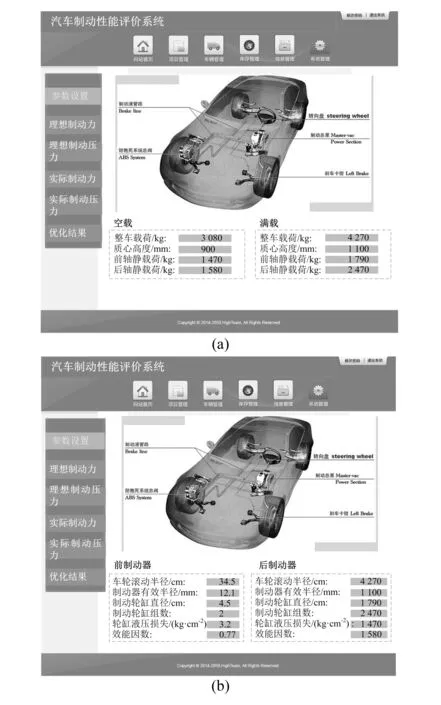
图2 参数输入界面

参数设置完成后，点击系统界面左侧“理想制动力”功能区域，系统自动显示理想制动力分配图以及理想制动力数据计算结果，如图3所示。

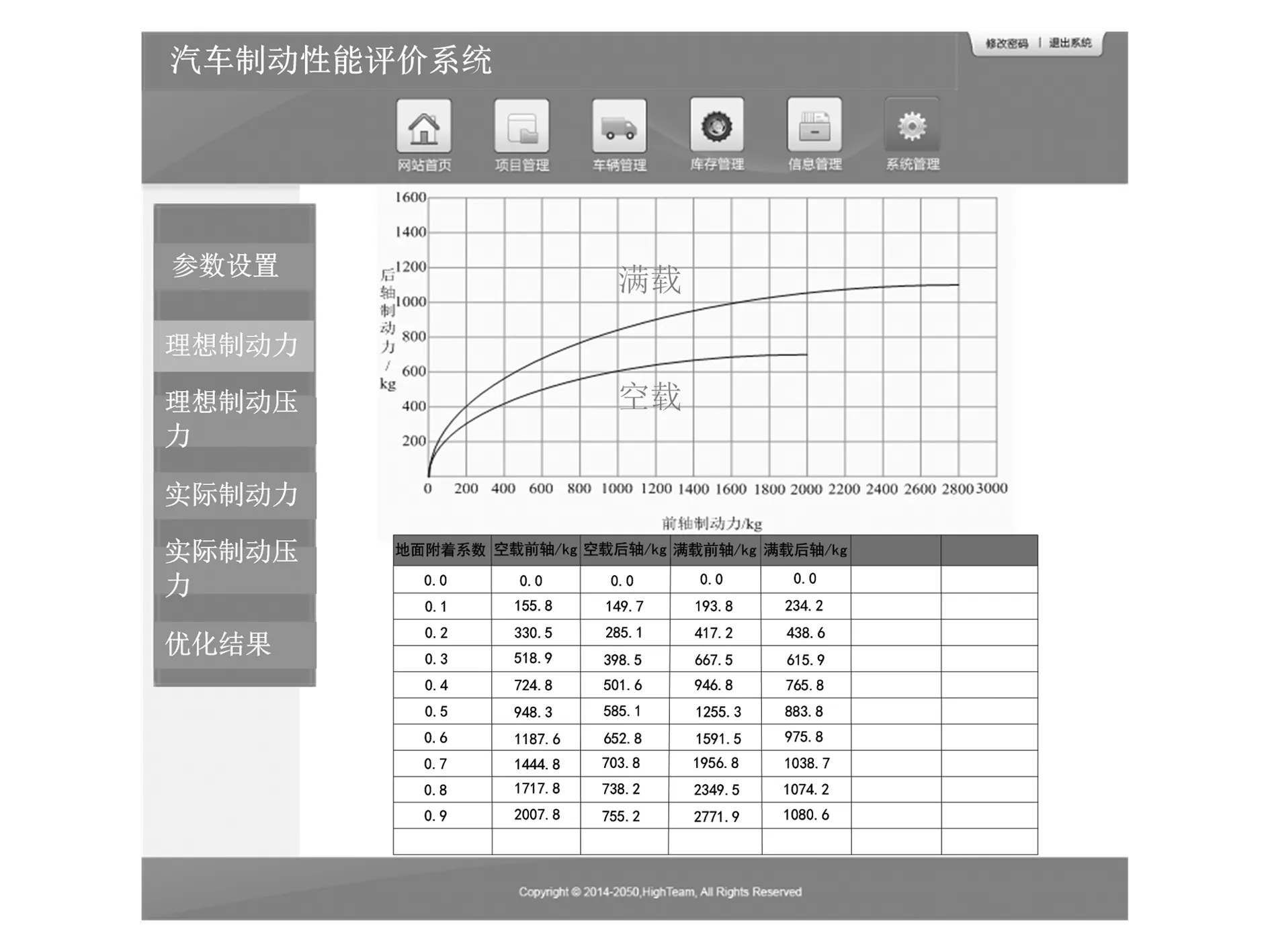
图3 理想制动力分配图及数据计算结果

点击系统界面左侧“理想制动压力”功能区域，系统自动显示理想制动压力分配图以及理想制动压力数据计算结果，如图4所示。

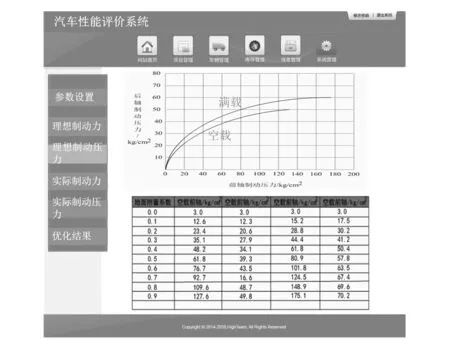
图4 理想制动压力分配图及数据计算结果

点击系统界面左侧“实际制动力”功能区域，系统自动显示该车辆实际制动力分配图，如图5所示。

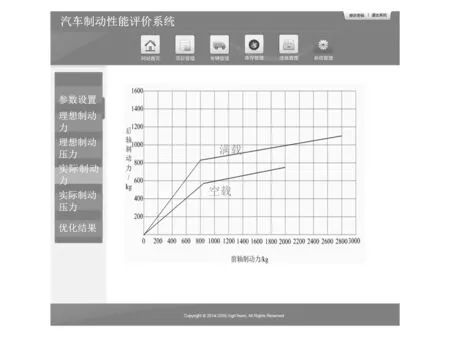
图5 实际制动力分配图

点击系统界面左侧“实际制动压力”功能区域，系统自动显示该车辆实际制动压力分配图，如图6所示。

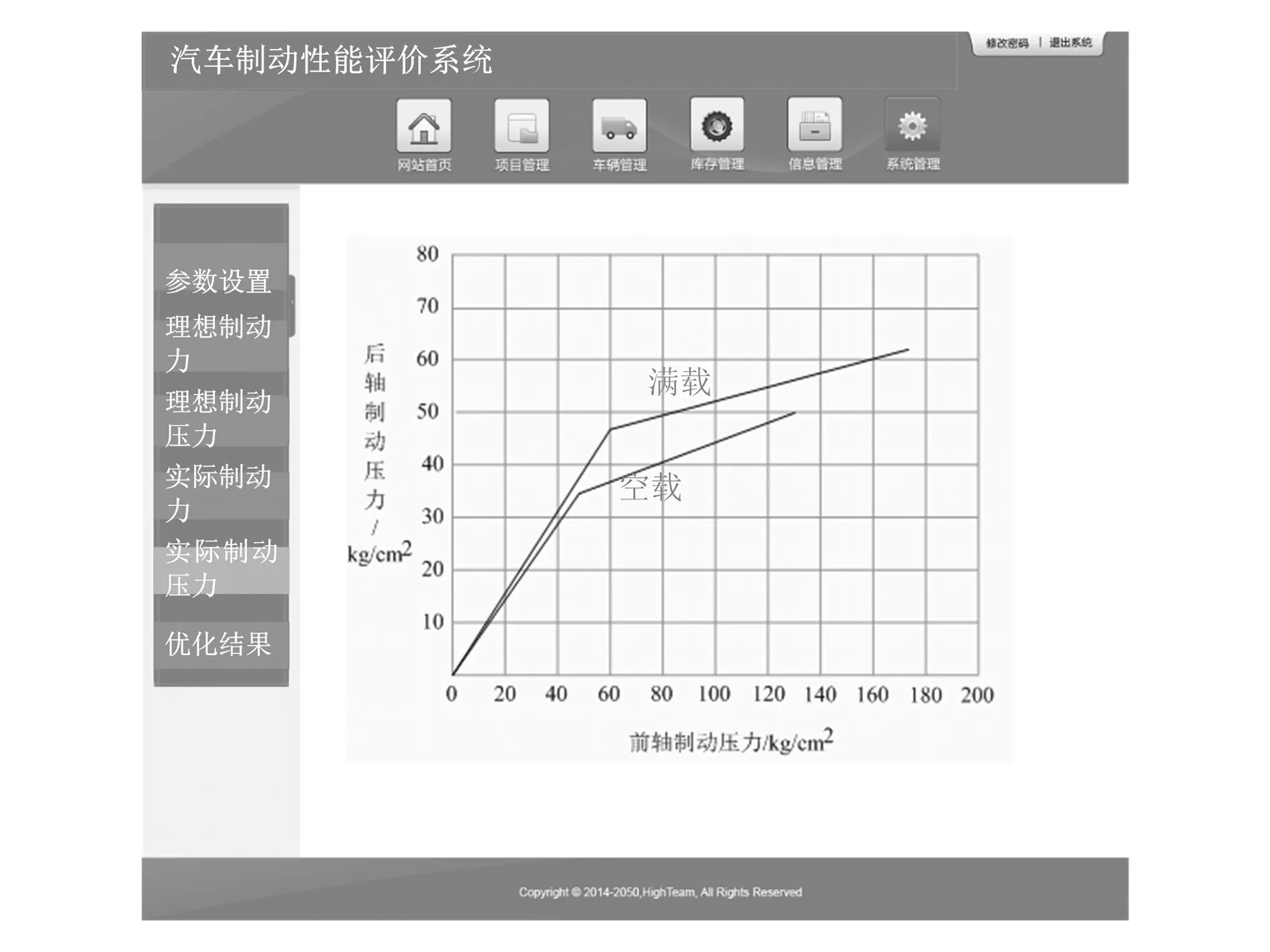
图6 实际制动压力分配图

将图3与图5、图4与图6相对比，可以看出实际制动力分配结果以及实际制动压力结果与理想制动力分配结果以及理想制动压力分配结果较为接近，说明该汽车具有较好的制动性能以及方向稳定性，在此基础上优化该汽车系统性能，点击系统左侧“优化结果”功能区域，可得空载权重为0、满载权重为1.0时汽车电子机械制动系统性能优化结果，如图7所示。

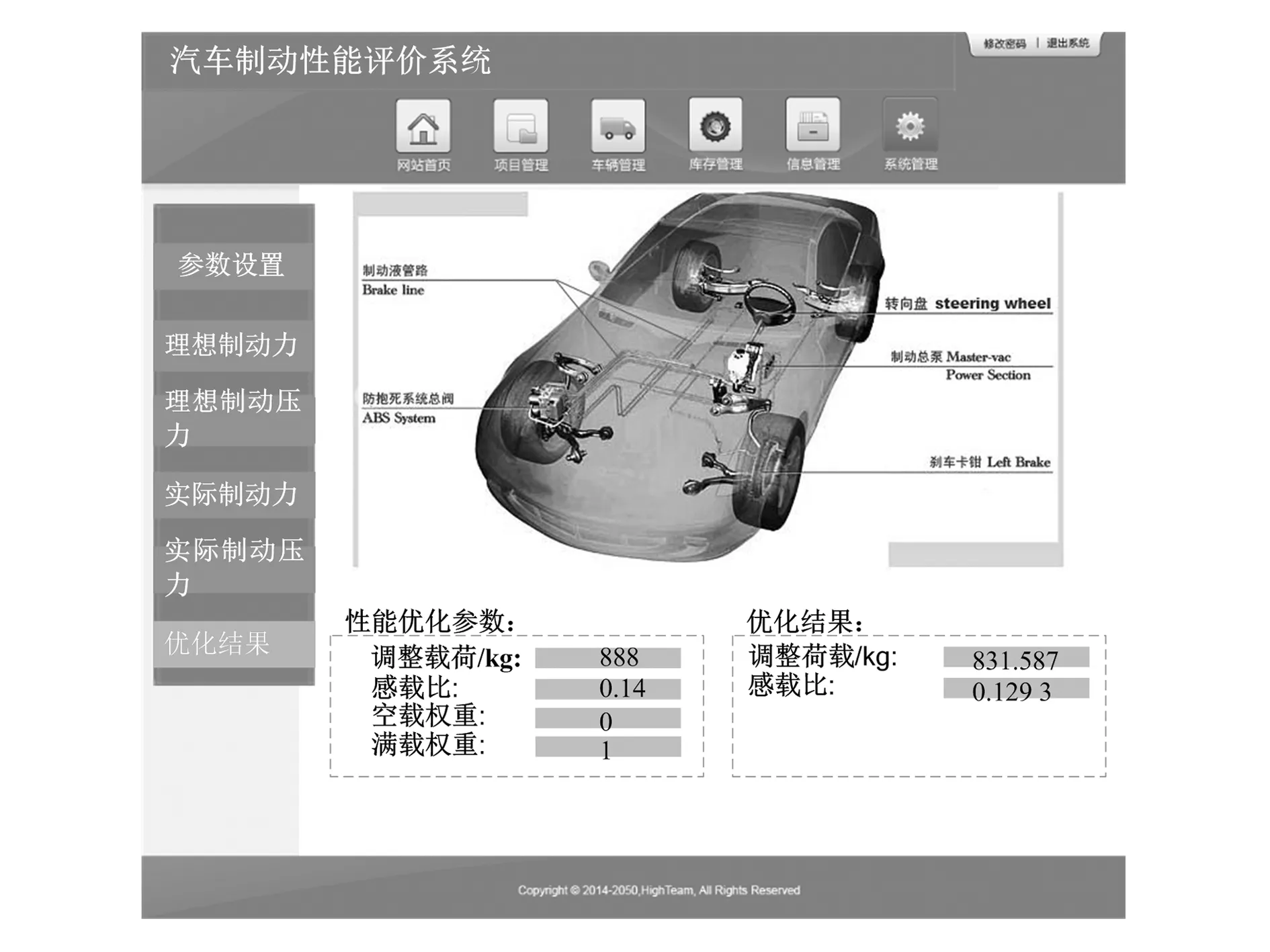
图7 汽车电子机械制动系统性能优化结果

改变空载以及满载权重，采用本文方法优化汽车电子机械制动系统性能，结果见表1。

根据以上性能优化结果绘制优化后制动系统制动力分配图，如图8所示。

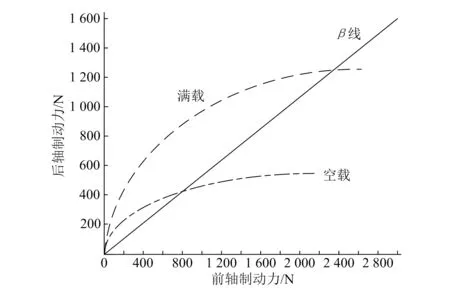
图8 优化后制动力分配图

图中β线为车辆制动力分配标准曲线，性能优化后汽车空载与满载均可满足附着系数要求，未出现汽车前后轮在相同时间抱死情况。汽车行驶过程中通常处于满载状态，当车辆满载行驶时，前后轴制动力接近于车辆制动力分配比，说明制动系统性能优化后，制动工况较为稳定，未出现侧滑问题，且制动过程中前轮抱死时的制动减速度大于后轮抱死时的制动减速度，验证了该汽车安全性得到了有效提高。

3 结束语

为提升汽车行驶安全性，本文提出了基于目标约束函数的汽车电子机械制动系统性能优化方法，首先建立制动系统性能优化目标函数以及约束函数，然后将制动系统性能优化问题转化为制动压力响应优化问题，建立汽车制动力综合平衡优化模型，最后通过对该模型进行求解实现了汽车电子机械制动系统性能优化。测试结果表明，优化后汽车制动性能明显提升，安全性也得以提升。