考虑杆塔平衡力的配网线路快速机械除冰次序优化

吕默影，陈苑婷，常建斌，郑腾飞

(国网浙江兰溪市供电有限公司，浙江 兰溪 321100 )

近年来我国电力技术高速发展，配网线路作为用户与电力系统连接的重要环节，在城市供电过程中占据重要地位，安全稳定的配网线路是电力系统良好运行的前提[1]。而在正常生态情况下自然灾害不可避免，覆冰灾害作为配网线路中最严重的灾害之一，将对电力系统运行产生直接影响[2]。配网线路的覆冰灾害会导致断线、杆塔倒塌以及电力系统崩溃等严重后果，因此有必要对配网线路进行合理除冰。配网线路除冰方法中机械除冰是较为常见且有效的方法，主要应用于地形特殊的配网线路。目前已有相关学者对机械除冰进行研究并取得了一定成果。文献[3]提出了采用遗传算法优化覆冰导线的清除次序。该方法考虑了输电线路的安全性，但不能有效地改善杆塔承受力不平衡的问题；文献[4]提出基于除冰机器人抗障碍干扰技术的配网线路快速机械除冰方法，根据自适应阈值小波变换算法提取障碍物图像边缘，利用图像特征匹配结果快速识别破冰障碍物。该方法能够高效识别障碍物，但由于该方法按照顺序除冰，未考虑杆塔承受的较大不平衡力，因此易发生杆塔倒塌等事故。

针对上述方法存在的问题，本文提出了考虑杆塔平衡力的配网线路快速机械除冰次序优化方法。将机械除冰过程中配网线路的杆塔所受不平衡力统计指标设定为次序优化目标，基于隐枚举法优化配网线路中各档线路覆冰清除次序，并通过实验验证该方法的有效性。

1 配网线路快速机械除冰机器人

1.1 报警装置设计及快速除冰机器人结构设计

将新型电子设备应用在配网线路机械除冰快速报警装置上，该装置由控制箱、板体、报警器等部件构成，结构如图1所示。

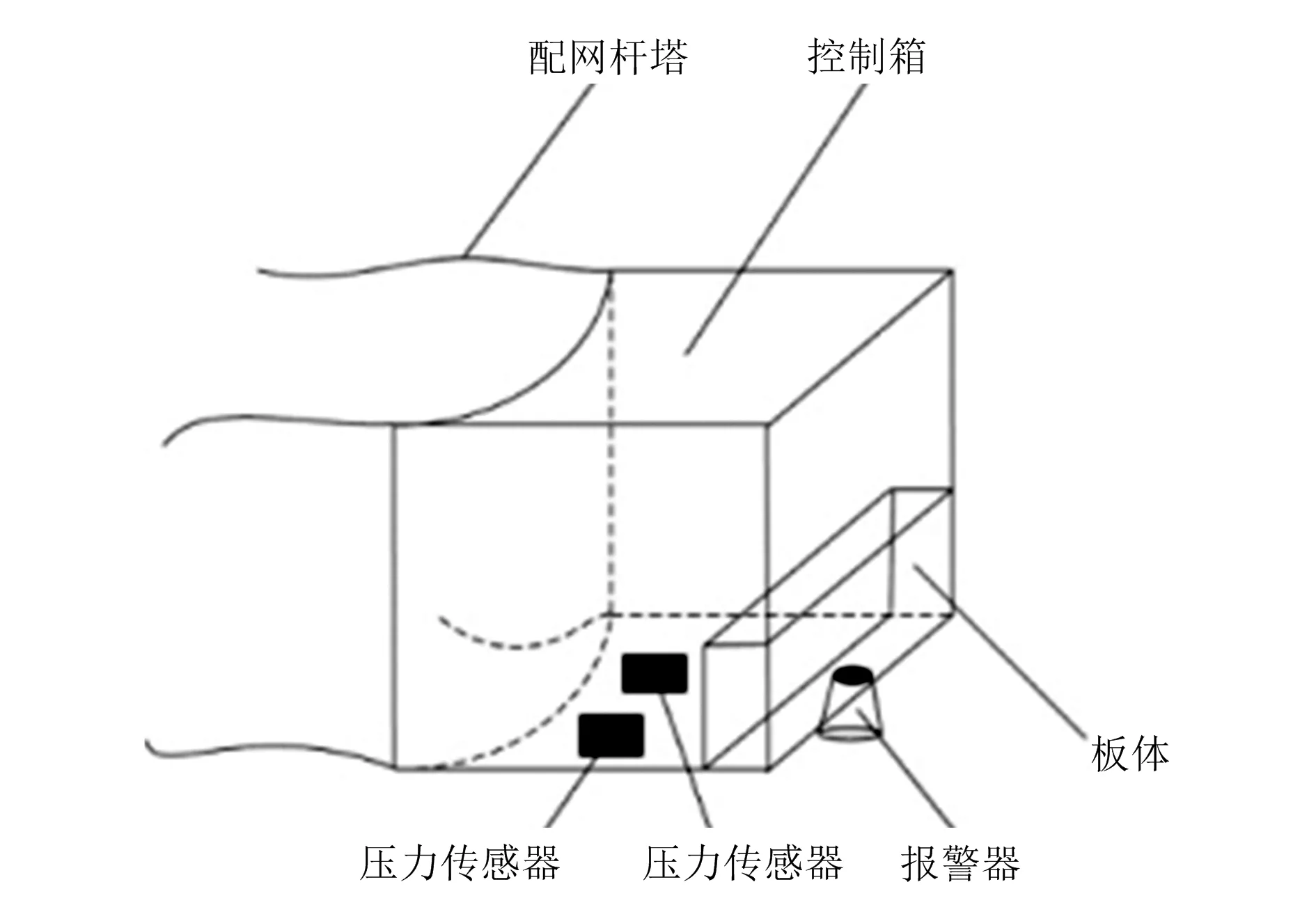
图1 机械除冰快速报警装置

利用捆绑带以及松紧带将报警装置的控制箱和板体固定于配网杆塔上，板体置于控制箱下侧，在板体与杆塔间设置压力传感器，压力传感器位于控制箱内，控制箱内设有报警箱，报警器位于报警箱底部，报警器与压力传感器分别与控制器的输入端、输出端相连接，控制器和蓄电池置于控制箱内。报警装置中设置2个压力传感器，分别位于板体上端、下端与板体间。控制器采用单片机或嵌入式系统。当配网线路中覆冰达到一定厚度时，会对报警装置的木板形成一定压力，压力传感器接收到压力信息后，发送信号至控制器，控制器发送控制脉冲信号至报警器，报警器将报警信息发送给机械除冰机器人，机器人立即对配网线路进行除冰。

本文所设计的快速机械除冰机器人采用双凹槽滑轮悬挂式行走机构，通过电机正反转完成行走动作。除冰结构上半部分采用高弹性弹簧，底部采用高速电机驱动，头部连接锋利的除冰刀刃，通过高弹性弹簧形变产生的拉力及高速电机运作产生的驱动力带动除冰冰刃运动，完成快速除冰。

1.2 快速机械除冰机器人

图2为配网线路快速机械除冰机器人外观图[5]，该除冰机器人可去除直径为8～15 cm配电线路覆冰，可在最大直径为60 mm的线路上作业，且在较为复杂的环境中除冰速度可达800 m/h[6]。机器人上安装了夜视灯，可保证在雾霾天气以及夜间能正常工作，并设置了视频模块以及远程遥控模块[7]，便于操作者在室内观察机器人除冰状态[8]、配网线路状况以及有效操控除冰机器人。

图2 配网线路快速机械除冰机器人

2 配网线路快速机械除冰次序优化

2.1 模型构建

在快速机械除冰过程中，机器人的自重会引发配网塔杆不平衡现象，严重威胁杆塔安全。将杆塔受单相导线作用的最大不平衡力与该导线最大张力之比作为评价杆塔安全程度的直接指标(FC)，利用该指标评价快速机械除冰时杆塔的安全性。杆塔安全程度受快速机械除冰次序影响极大，将快速机械除冰过程中杆塔所受不平衡力最小的除冰次序作为快速机械除冰的最优除冰次序[9]。除冰次序优化目标函数f的公式如下：

f=min(FC)

(1)

i=1,2,…,n;j=1,2,…,n+1

(2)

ΔFi,j=Fi,j-Fi+1,j

(3)

式中：i为杆塔编号；j为除冰次序中依次清除覆冰档的编号，杆塔号编号过程中配网线路耐张段周围的耐张塔不在编号内；n为耐张段内杆塔数；FS为单相导线最大使用张力；Fi,j与ΔFi,j分别为第j档除冰后第i基杆塔所受水平张力以及不平衡力。

杆塔水平张力Fi,j公式如下：

Fi,j=ηi,jA

(4)

式中：ηi,j为第j档除冰后第i基杆塔所受水平应力；A为杆塔导线截面积。

快速机械除冰过程中，利用连续档导线除冰模型获取每一相导线应力[10]，第i基杆塔导线增量公式如下：

(5)

式中：η0为连续档架线时导线所受水平应力；ηi为第i基杆塔悬挂点偏移量；t为连续档架线时气温；t0为初始气温；γ0为初始比载；γi为连续档架线时初始比载；ηi0为气温为t0、比载为γ0情况下第i基杆塔中导线所受水平应力；li0与βi0分别为第i基杆塔架线时档距以及高度差；Δli为连续档架线悬垂串位于中垂位置时档距增长量，当档距缩短时，Δli为负值；Δhi为连续档杆塔两端悬垂串偏斜后悬挂点间高度差变化量，在左悬挂点低于右悬挂点情况下，Δhi与βi0均为正值；E为弹性系数；σ为温度线膨胀系数。

η与δi关系如下：

(6)

式中：δi，δi-1分别为第i,i-1基杆塔上悬挂点所偏移距离；α为杆塔中悬垂绝缘子串长度。在杆塔两端耐张区耐张塔中δi=0，δn=0；配网线路应力η(i+1)0与悬挂点偏移距离δi关系如下：

(7)

其中：

δi=Δl1+Δl2+…+Δli=δi-1+Δli

(8)

利用式(1)～式(8)构建考虑杆塔平衡力的配网线路快速机械除冰次序优化模型。

2.2 基于隐枚举法的快速机械除冰次序优化

快速机械除冰次序优化模型包括多种非线性约束，为典型的非线性NP问题，为快速、准确获取最优除冰次序，采用隐枚举法对快速机械除冰次序优化问题进行求解。

隐枚举法求解快速机械除冰次序优化问题步骤如下：

步骤1，初始化处理。输入快速机械除冰各档档距以及覆冰厚度，并输入档数n，将除冰轮次a初始化，即设置除冰轮次a=1。判断除冰过程中安全指标FC结果并建立矩阵，矩阵分别为A,B,C,其中矩阵C的行数为1。

当实际已除冰档号矩阵A中存在0元素时，表示此处除冰档号未被确定。

步骤2，当除冰轮次a=1时，求解配网线路耐张段内通过各档进行除冰后最大安全指标FC值，即：求解除冰轮次为1且除冰档数为1时最大安全指标FC值；求解除冰轮次为1且除冰档数为2时的最大安全指标FC值；……以此类推，最终获取除冰轮次为1且除冰档数为n的最大安全指标FC值。以上计算结果为矩阵C的行,其必须与各除冰档数依次对应。矩阵A中实际已除冰档号元素依次对应到矩阵C的行元素的对应位置，将矩阵内序号依次排序并标记，被标记的元素表示已计算。

步骤3，将矩阵A中元素写入矩阵B中，并将矩阵B中元素依据序号从小到大进行排列。搜索矩阵C中是否存在已计算过的除冰档号，并获取相应档号的FC值。将已除冰档号依照从小到大顺序排列后进行标记，除冰次序不同时，在排序后可能会出现相同标记。

步骤4，当矩阵C总行数为(b+1)时，将档号按照从1至n的顺序依次确认该档号是否为已除冰档号。当该档号为已除冰档号时，将矩阵C的b行存入该档号的列；若该档号为未除冰档号时，求解该档号的最大FC值，发送至矩阵C的b行中该档号相对应位置，将以上情况标记至矩阵C相同行中，将b标记为zl。

步骤5，将矩阵C中zl行获取FC值的结果中非0的最小值标记为min，将非0的最小值在矩阵C中相对应的列号发送至已除冰档号矩阵A(1,a)中。当除冰轮次a为1时，实际除冰档号为第一轮，设定除冰轮次为a+1，并返回至步骤3，直到除冰轮次为1，运行步骤6。

步骤6，将已除冰档号矩阵A发送至过渡判断矩阵B中，将矩阵B中B(1,a)与B(1,a-1)位置的除冰档号设置为0，同时将矩阵B中元素依据从小到大顺序进行排列并作出标记。在矩阵C中依次找出标记后的行，并将行号标记为z3。将min和C(z3,A(1,a-1))进行对比，若min>C(z3,A(1,a-1))，则在C(z3,A(1,a-1))中加入min值，使矩阵A(1,a)、A(1,a-1)位置元素为0，将除冰轮次设置为a-1，并返回至步骤3。若min≤C(z3,A(1,a-1))，将矩阵C位置中第一个非零元素列号发送至矩阵A(1,a)中，并转入步骤7。

步骤7，将除冰轮次a与档数n进行比较，当a=n时，说明实际已除冰档号矩阵排序即为快速机械除冰最优次序，算法结束；若a≠n，则将除冰轮次设置为a+1，返回至步骤3。

将配网线路除冰次序优化目标函数与最优除冰次序求解结果相结合，设定隐枚举法获取最优除冰次序的约束条件如下。

约束条件1：设定最大FC值。

当配网线路耐张段中除冰档数为n时,共有n!种除冰次序。在进行快速机械除冰时，FC值所对应的除冰次序、除冰轮次大小均为未知，因此设定约束条件中FC值在计算过程中有所改变，直至获取到实际最大值为止。当计算结果小于最大值时，无需更新FC值，在保证计算结果准确的前提下有效简化了计算过程。

约束条件2：标记FC值计算结果。

在优化除冰次序的过程中，标记已计算的除冰档号，无需重复计算该档号除冰的FC值，避免次序优化过程中的多次计算，依据次序由小至大进行排序，从而提高计算效率。

3 实验分析

为验证本文提出的考虑杆塔平衡力的配网线路快速机械除冰次序优化方法(以下简称所提方法)的有效性，以配网线路除冰时长及除冰次序优化情况为评价指标，在MATLAB2018仿真实验平台搭建配网线路模型以及覆冰场景进行仿真实验。

以4条连续档配网线路为例进行实验。4条线路档距以及高差(高度差)参数见表1。架线温度与除冰温度分别为0 ℃和-5 ℃；绝缘子串长度为5.3 m，质量为2 300 N；4条线路架线应力分别为52.67，48.67，47.68以及52.67 N/mm2。

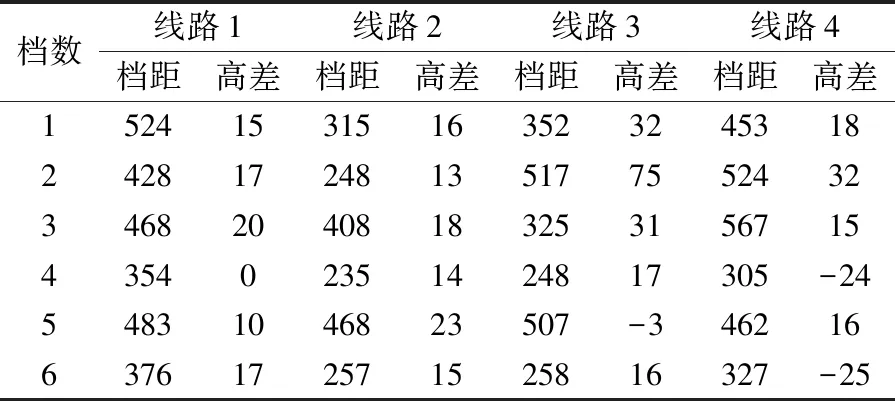
表1 仿真实验参数 m

在仿真平台中设置配网线路覆冰厚度为25 mm，在此情况下测试所提方法的除冰时长，并采用文献[3]、文献[4]方法作为对照组，3种方法的除冰时长对比结果如图3所示。

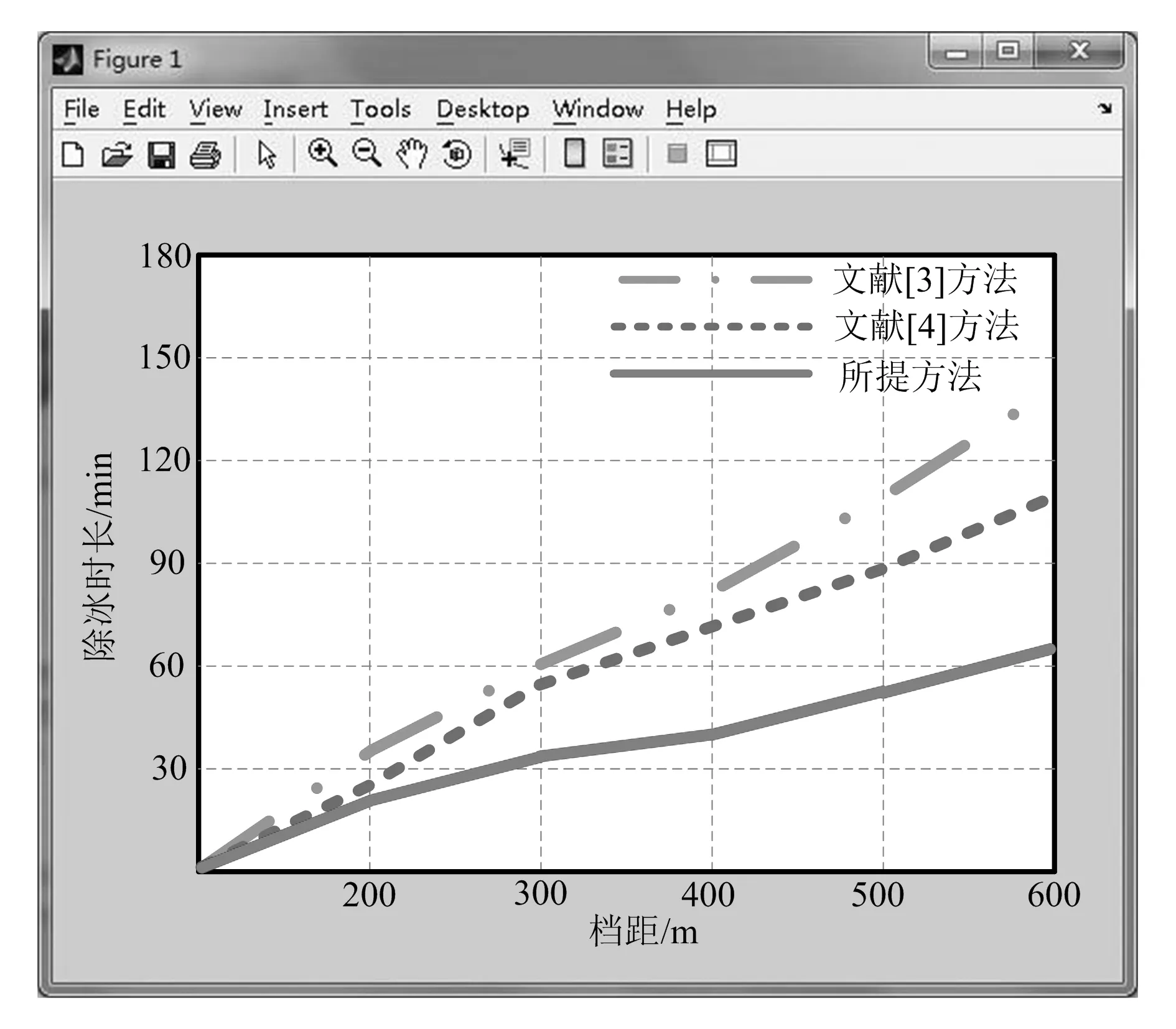
图3 3种方法除冰时长对比结果

由图3实验结果可知，在档距为600 m的输电线路中，文献[3]方法的除冰时长为140 min，文献[4]方法的除冰时长为110 min，而所提方法的除冰时长仅为65 min，远远低于前两种方法。实验结果说明所提方法能够有效减少机械除冰耗时，提高除冰效率，实现配网线路快速除冰。

在验证了机械除冰效率的基础上，验证所提方法的除冰次序优化效果。在仿真平台中设置覆冰厚度分别为30，35 mm，在这两种情况下对配网线路按照正序、逆序分别进行快速机械除冰，再依据所提方法、文献[3]和文献[4]方法进行快速机械除冰,除冰次序优化结果见表2、表3所示。

表2、表3的实验结果显示，在不同覆冰厚度情况下，采用所提方法对配网线路快速机械除冰次序进行优化，4条线路杆塔所受不平衡力百分比均为最低，验证了所提方法进行除冰次序优化的有效性。

为进一步验证采用所提方法对配网线路快速机械除冰次序进行优化后杆塔所受不平衡力的改善情况，对比分析覆冰厚度为30，35 mm时3种方法对4条线路除冰次序优化后的不平衡力百分比降低率，如图4、图5所示。

由图4、图5实验结果可以看出，采用所提方法对配网线路快速机械除冰次序进行优化，不平衡力降低率明显高于文献[3]和文献[4]方法。在覆冰厚度为30 mm时，所提方法与正序以及逆序相比不平衡力降低率均高于50%；在覆冰厚度为35 mm时，所提方法与正序以及逆序相比不平衡力降低率均高于41%。实验结果说明采用所提方法对配网线路快速机械除冰次序进行优化，可有效降低杆塔所受不平衡力，提升除冰过程中配网线路的安全性。

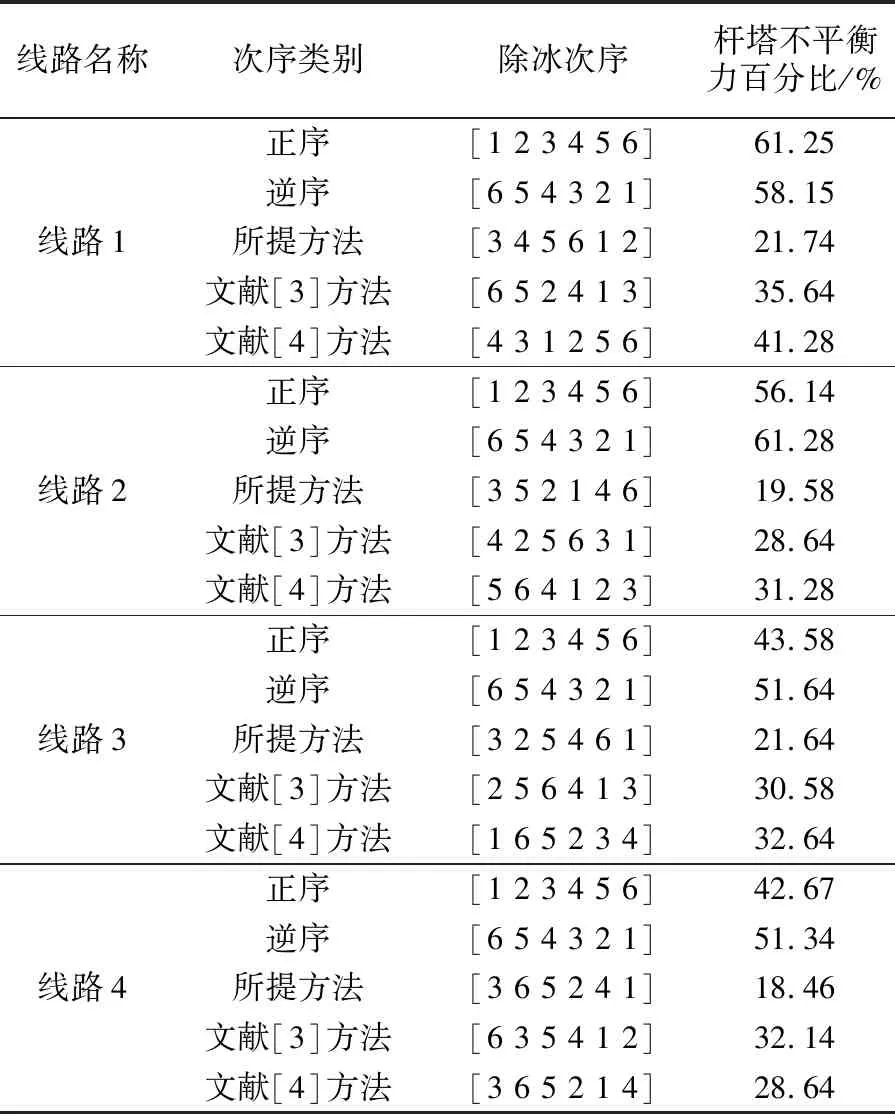
表2 覆冰厚度为30 mm时除冰次序优化结果

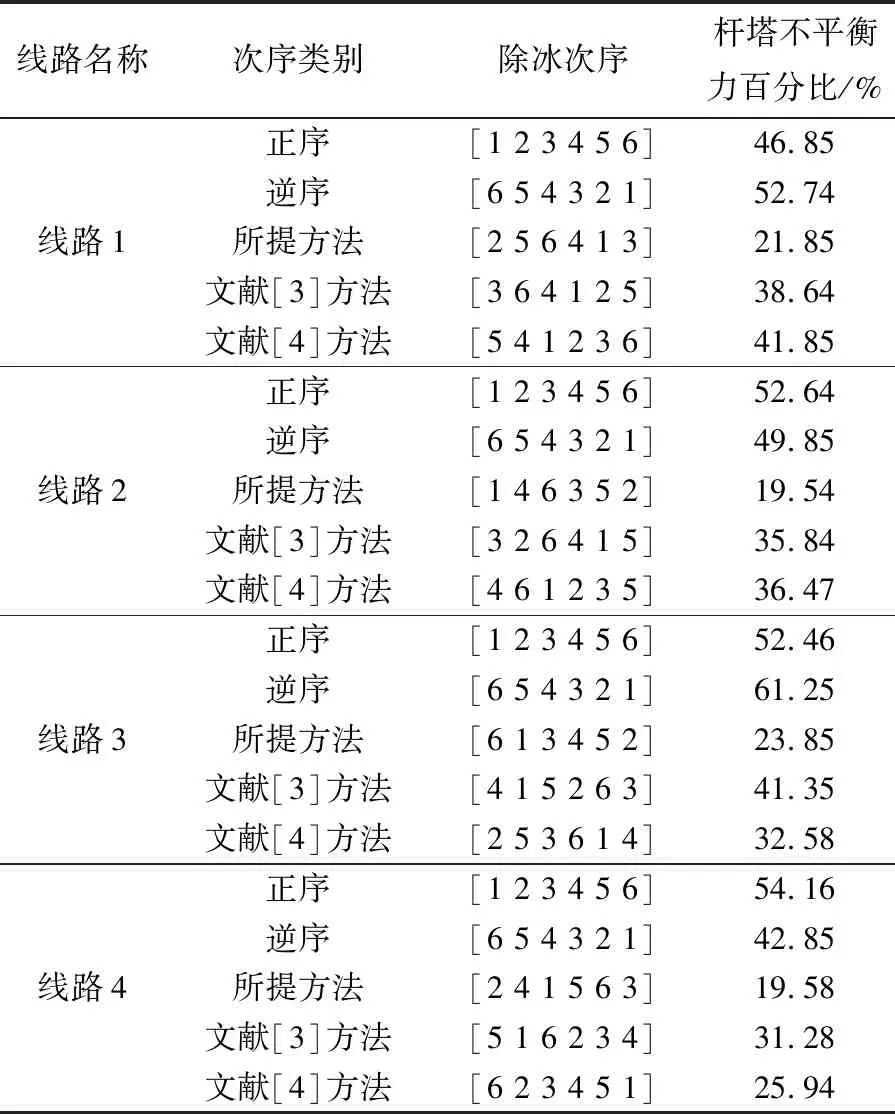
表3 覆冰厚度为35 mm时除冰次序优化结果

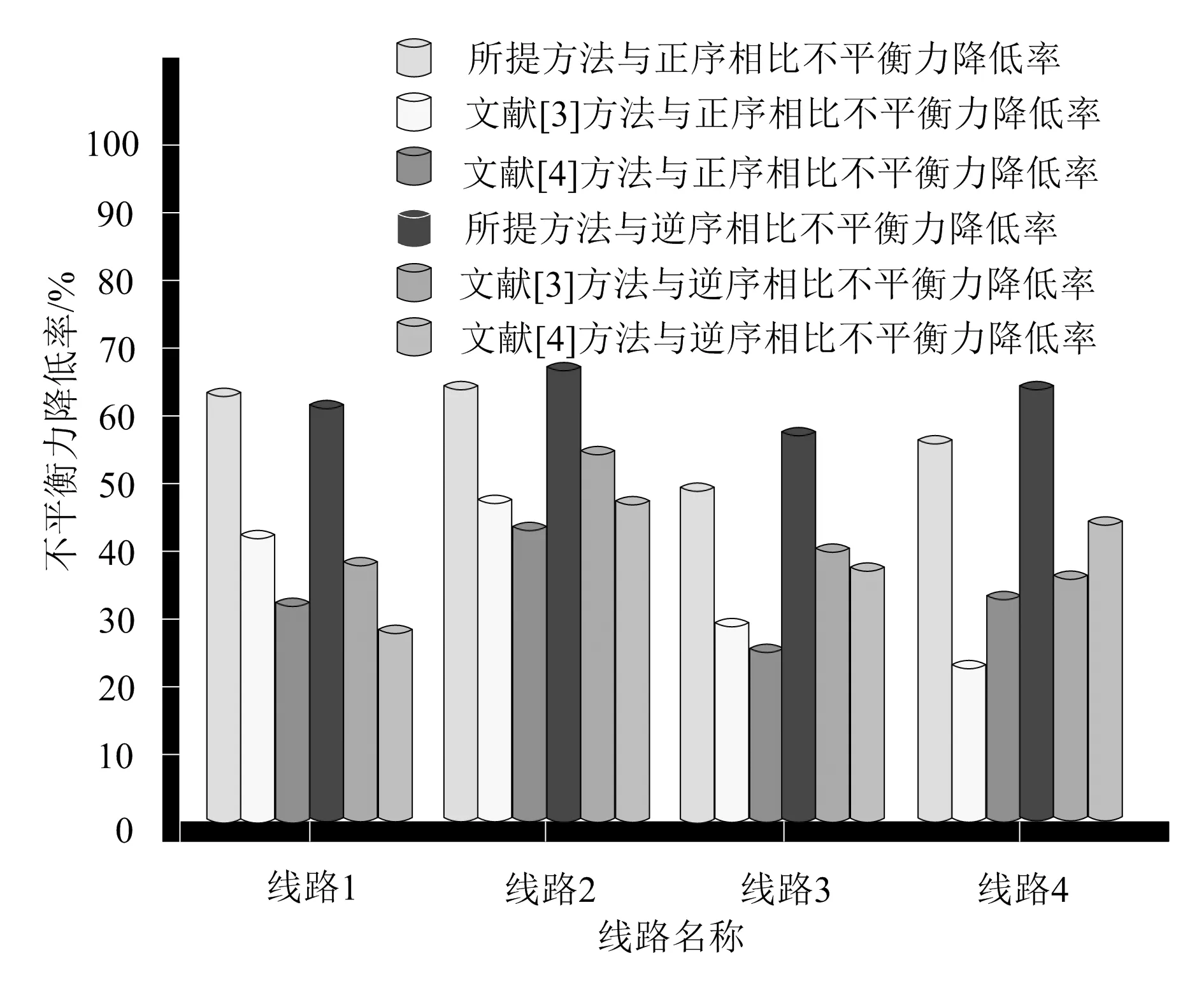
图4 覆冰厚度为30 mm时不平衡力降低率对比

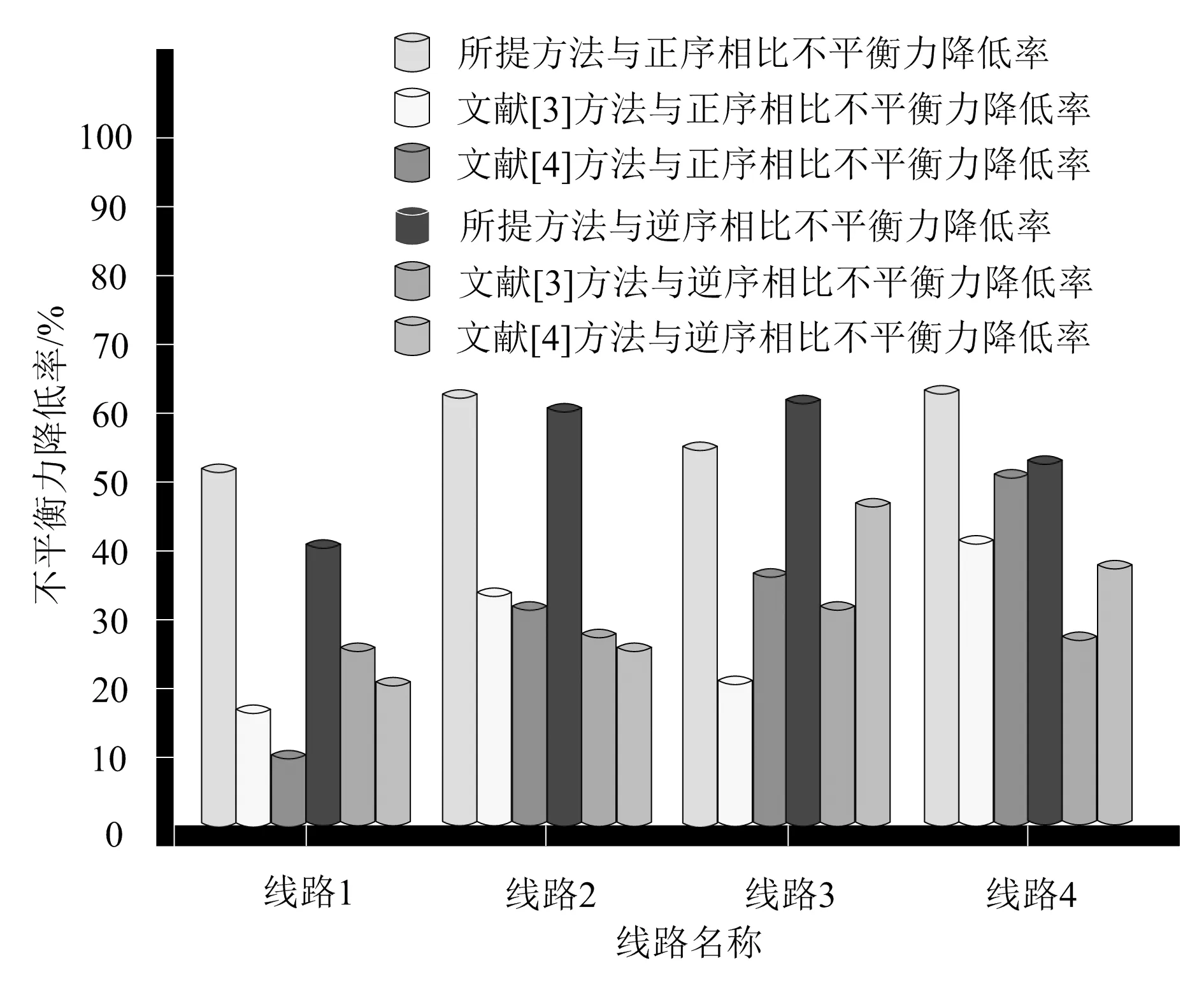
图5 覆冰厚度为35 mm时不平衡力降低率对比

4 结束语

为提升机械除冰的安全性，本文提出考虑杆塔平衡力的配网线路快速机械除冰次序优化方法。根据杆塔所受不平衡力最小的除冰次序，建立机械除冰次序优化模型，并通过隐枚举法对机械除冰次序进行优化。为验证所提方法的有效性，设计仿真实验。实验结果表明，与传统方法相比，利用该方法对配网线路中快速机械除冰次序进行优化，能有效降低快速机械除冰过程中杆塔所受不平衡力，为实际快速机械除冰提供了有效参考。