电渗析过程传质模型的研究进展

祝海涛，杨波，高从堦

（1浙江工业大学膜分离与水科学技术中心，浙江杭州310014；2杭州水处理技术研究开发中心有限公司，浙江杭州310012）

电渗析技术具有能耗低、药剂耗量少、对盐含量适应性强、预处理简单、易于实现机械自动化且环境污染小等优点[1-3]，在食品、医药、化工等领域的分离提纯中发挥重要作用。为了提高电渗析分离性能及电流效率，需进一步优化电渗析结构设计和操作工艺。但是，电渗析传质过程复杂，多参数关联，从实验角度对其进行全面深入研究的难度大，从而限制电渗析分离工艺的有效优化。近年来，相关科研人员尝试设计了很多数学模型以模拟基于电渗析的物质分离过程，结合流动状态、电流密度等探讨离子和其他不带电物质的传递规律[4-9]，并在此基础上确定分离最优的操作策略。因此，传质模型化为电渗析传质的理论和实验研究提供了一条直接有效的途径。基于电渗析分离过程的传质模型一方面能够准确预测电渗析系统中物质传递行为以及隔室和膜中的离子浓度分布、电势分布等[10-13]，另一方面能够导向性地优化电渗析分离的操作工艺等[14-17]。通常，电渗析过程中的传递现象主要包括离子交换膜之间的对流传递、离子定向朝着或透过膜的电迁移传递和扩散传递，以及浓差极化、水动力学现象、电解质-膜平衡等复杂过程[18-20]，因此电渗析过程传质模型化较其他膜过程更为复杂。目前，用于描述电渗析过程的传质模型主要有Maxwell-Stefan 模型、Nernst-Planck 模型、Kedem-Katchalsky模型、模糊逻辑模型、人工神经网络模型和半经验模型等。本文对基于不同理论方程的电渗析传质模型研究进行了综述，分析了电渗析传质模型的应用优势及不足并对未来研究方向进行了展望。

1 电渗析简述

电渗析这个概念最早由Maigrot 和Sabates 在1890 年提出[21]，到1911 年以后建立了电渗析理论并制备出离子交换膜，1950 年Juda 和McRay 制造了多隔室电渗析组器，1954 年美国Ionic 公司在沙特阿美石油公司建成第一套电渗析脱盐装置[22]，目前电渗析已发展成为在饮料加工、药物生产、苦咸水/海水脱盐、工业废水处理以及资源回收等领域的一个重要化工单元过程[23-25]。电渗析技术在水处理方面最突出的优点有膜使用寿命长、耐酸碱性强、不需要严格的前处理、较反渗透膜具有更高的水回收率等。近年来电渗析研究主要集中于高性能离子交换膜设计与制备，离子交换膜抗污染性，选择性电渗析、双极膜电渗析和反向电渗析的应用，电渗析脱盐过程系统能耗以及基于电渗析过程的数学传质模型等。高性能离子交换膜研究主要是提高膜的电化学性能和选择透过性，另外一价、二价选择性膜、双极膜等特殊离子交换膜的成功开发使电渗析在分盐浓缩、盐制酸碱等领域中得到广泛应用[26]。而膜污染问题一直是限制电渗析放大与应用的主要难题，目前研究人员通过微波、磁场、超声波、电脉冲等外力来降低膜污堵并提高脱盐率[25-26]。在电渗析能耗方面，研究人员将风能、太阳能、地热能等可再生能源以及浓差转化成电能的反向电渗析与电渗析脱盐系统集成，使电渗析技术更节能环保[27-28]。基于电渗析传质过程的数学模型不仅可以有效研究各种因素对电渗析能效的影响，还能准确预测电渗析分离效果与能耗，已成为最近几年电渗析方向的研究热点[29-31]。

电渗析是通过直流电场驱动使溶液中阴阳离子选择性透过离子交换膜，实现离子从溶液中分离的一种物理化学过程[25,31]，可以达到料液的浓缩、淡化以及盐和有机物的分离等目的。电渗析工作原理如图1所示，一个电渗析单元通常由一系列阴阳离子交换膜、淡水室、浓水室以及两端电极组成，电极间施加电压后，阳离子向阴极方向迁移，阴离子向阳极方向迁移，阳离子交换膜上固定的活性基带负电荷，允许阳离子透过而阻止阴离子透过；阴离子交换膜正好相反。这个迁移过程使浓水室中盐浓度增加，淡水室中盐浓度降低。数学传质模型也是基于该传递原理建立，用于描述和模拟离子在膜相、主体溶液相和扩散层中的传递和分布情况[31-33]，为设计开发新的离子交换膜和装置以及电渗析分离工艺优化提供理论指导，以满足不同的水处理应用要求，包括果汁去酸化、重金属去除、废水零液排放等。

图1 电渗析工作原理

2 模型理论基础

在对电渗析分离过程进行建模时，首先需明确电渗析过程物质传递原理，然后利用热力学方程、电化学方程以及物质传递方程等描述物质在电场作用下的迁移情况。在电渗析两端电极上施加电压后，电解质溶液和离子交换膜受到电场作用，由离子传导引发电流传递。离子传递通量一般由对流、扩散和电迁移三部分组成。在膜中离子传递主要由电迁移控制，电迁移通量与离子所带电荷数、离子迁移率、离子浓度和电势梯度等有关；电解质溶液中的对流和扩散对离子传递也有很大影响，这取决于流体平均流速和化学势梯度[17,32]；在离子交换膜边界的传递行为则更为复杂，这是因为还需通过与水动力学方程联立求解和分析，模拟物质在扩散层中的传递行为，描述膜边界处的浓度梯度、电势分布，以及研究电渗析实际应用中可能发生的极化现象等[33-34]。另外，电渗析传质过程还包含水分子在离子交换膜间的传递，这主要由离子的水合作用和自身的迁移所引起[30,35]。

为了更准确地描述电渗析过程中的物质传递现象，研究人员通过建立数学模型并配合电渗析实验进行进一步传质研究[36-37]。如图2 所示，结合电渗析分离原理将实际传递过程简化并分解，采用相关方程描述各个物理化学过程。研究人员最初建立的传质模型多为经验性模型，一般通过简单的数学工具与实验结果结合得到。虽然这类模型的建立和求解较为简单，但在详尽描述电渗析传质过程中受到很大限制[38]。后来研究人员采用非平衡热力学方程（如Maxwell-Stefan、Nernst-Planck方程等）并结合离子在电渗析中传递的相关物理参数建立数学传质模型，使其更接近实际电渗析传质过程。近年来，电渗析传质模型化研究更系统深入，不仅关注物质在电驱动膜系统、主体溶液及膜边界层中的传递行为，还对整个电渗析组器的物质传递、电流效率等进行研究[39-41]。随着学科的交叉融合以及计算模拟技术的发展，如模糊逻辑系统、人工神经网络等理论模型也被开发并应用于电渗析传质过程的研究。

图2 电渗析分离原理及模型化

3 电渗析过程传质模型

3.1 Maxwell-Stefan模型

非平衡热力学理论一般采用由耗散函数推导所得的现象学方程和施加的驱动力来描述膜渗透通量，再通过数学工具把膜间的浓度差或电势差与通量关联起来[38]。其中，Maxwell-Stefan 传质模型包含严格的微分方程，可以预测性地描述几乎所有传递现象。Kraaijeveld等[42]采用Maxwell-Stefan传质模型描述NaCl-HCl体系和氨基酸体系的电渗析过程，研究发现根据分离实验得到的膜中反离子扩散系数、极化层厚度、电流效率和黏性流渗透率等参数都在模拟结果预期范围内，而氨基酸分离体系由于增加了系统复杂性导致无法通过Maxwell-Stefan 模型分析电渗析传质过程。因此，Maxwell-Stefan 传质模型主要应用于简单的水分子、盐离子迁移量的描述或预测。Pintauro 等[43]对传递参数和热力学分布系数的确定做了深入研究，针对NaCl-H2ONafion离子交换膜系统，在不同电解质浓度下通过电渗析实验数据和数学传质模型的匹配，确定了平衡系数和传质参数，并预测了溶液的浓度和膜电导的变化趋势。Tedesco 等[30]采用Maxwell-Stefan 方程，如式(1)所示，研究离子与水及离子与膜之间的相互作用。将水看作连续流体并忽略离子间摩擦后，模型方程在x方向可变为式(2)。式中，μi表示离子i的电化学势，R表示气体常数，T表示温度，j表示水或膜或另一种离子，fi-j表示i和j之间的摩擦系数，vi和vj分别表示i和j的速率，vF表示流体在膜中的流速，Di-F表示离子在流体中的扩散系数，fi-m表示离子i和膜之间摩擦系数，ci表示离子浓度，zi表示量纲为1 电势。通过模拟计算证明水渗透对电渗析和反向电渗析都有明显影响，并且其渗透速率与反离子在同一数量级。

然而，Maxwell-Stefan 模型对电解质溶液相关参数依赖性大并且系数相互关联，若将相关传质系数进行简单设定，将导致其与实验过程中的参数不符，即Maxwell-Stefan 传质模型应用到电渗析过程中的主要问题是缺乏与实际对应的扩散系数或热力学性能参数。因此，需要对扩散系数等相关参数进行修正，使理论推算值与实验值更相符，但这又会导致其他参数偏离实际值。Wesselingh 等[44]将溶液主体中的扩散系数通过“曲折度”函数与膜中的扩散系数关联，从而估算离子在膜中的扩散系数，但由此得到的膜电势降很高，不符合实际，而且即使采用修正因子也不能准确预估相关系统性能，说明电渗析过程中某些现象因Maxwell-Stefan 的简化而未能体现。因此，后来针对该模型的应用较少，多采用其他模型方程模拟电渗析过程传质行为。

3.2 Nernst-Planck模型

目前被广泛使用的Nernst-Planck 方程易与水动力学方程、连续方程和化学反应方程等联立耦合，较Maxwell-Stefan 方程能更简便有效地模拟电渗析的传质过程，通过对电渗析重复单元进行几何模型化（图3），更准确地描述溶液、膜以及扩散边界层中的离子传质行为。所以，近年来有关电渗析传质所建立的数学模型大多基于Nernst-Planck方程，推断今后电渗析传质模型的研究重点也将是基于该方程进行模型优化。

Nernst-Planck 模型基于离子通量独立性原则，即不受其他离子电势梯度影响，不考虑离子间相互作用系数。因此，每种离子对应一个扩散系数，使其与水动力学方程、连续方程和化学反应方程等联立耦合后更易求解[45]。Jiang等[46]在Nernst-Planck方程的基础上，如式(3)所示，利用离子在膜中迁移的毛细管理论建立电渗析过程水迁移模型，如式(4)所示。式中，Di表示离子i在水中的扩散系数，F表示法拉第常数，V代表电渗析过程淡室中水减少速率，q表示表面电荷，r表示毛细管壁到溶液距离，η表示溶液动力黏度，i表示电流密度，l为毛细管长度，c¯1表示面向淡室的膜表面离子i浓度，c¯2表示面向浓室的膜表面离子i浓度。式(4)中，等号右边两项分别代表电渗透和渗透压差引起的水迁移，通过计算分析明确电流密度、离子电荷数、溶液动力黏度、溶液浓度等对水迁移的影响规律。

图3 电渗析单元几何模型建立［29］

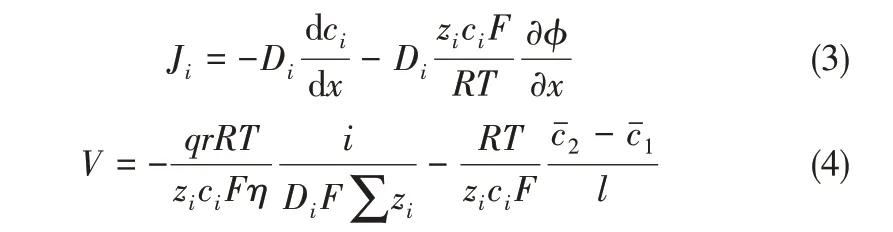
Casas 等[47]已将基于Nernst-Planck 方程的数学模型应用于电渗析浓缩反渗透浓水的中试项目，将Nernst-Planck 方程和质量守恒方程联立，通过进水浓度、流速、电流密度等工艺参数的输入，预测了整个电渗析系统的性能与运行结果，尽管模型部分设计基于理想状态，但模拟结果仍能与实验数据较好吻合。研究结果表明Nernst-Planck 传质模型能较准确地描述电渗析的传质过程，并且模拟结果可用于指导电渗析实验的设计和操作以及解释电渗析分离或浓缩过程中不同因素对结果的影响。

但是，由于Nernst-Planck 模型没有考虑离子间的相互作用，所以该模型一般只适用于稀溶液。Krishna[48]认为Nernst-Planck 方程要在盐浓度低于0.1kmol/m3条 件 下 才 可 应 用。Lee 等[49]将Nernst-Planck模型进行了优化，使其浓度适用范围提高至0.5kmol/m3。Fidaleo 等[6,15]通过基于电解质回收的电渗析实验所建立的模型能较准确地模拟浓度为1.0kmol/m3以上原料液的脱盐过程，但是模拟结果与实验偏差逐渐变大。因此，后续需要进一步合理优化Nernst-Planck 模型，从而扩大其实际应用范围。研究发现，将其与相关经验公式联立，能更准确地预测较高盐浓度的离子传递行为，并通过电渗析脱盐实验得到了验证。另外，Tedesco 等[29]对电渗析建立了二维Nernst-Planck 模型，同时考虑了膜的非理想行为（同名离子的传递）。该模型通过与系统几何参数、膜电荷密度、离子在隔室和膜中的扩散系数等相关函数预测离子交换膜的膜电阻和选择性，并评估了分离过程整个电渗析的系统能耗和反向电渗析的功率密度，发现由考虑同名离子传递的改进模型计算的电渗析能耗和反向电渗析的功率密度分别为原模型计算值的3倍和80%，且更符合实验值。因此，对于Nernst-Planck 模型另一个优化方向是将同名离子传递、水迁移等影响因素纳入其中，使建立的模型拟合结果与实际电渗析应用更加接近。

3.3 Kedem-Katchalsky模型

Kedem-Katchalsky模型是以不可逆热力学形式将膜视为在两个均匀区域之间的一个几何过渡区或非均匀区，并假定某一物质通量等于各驱动力总和乘以对应系数，通过确定模型方程中离子交换膜和电解质溶液的传递参数，模拟离子、水分子等传递通量[50]。Kedem-Katchalsky 模型考虑了溶液中各物质通量的相互影响，使该模型相较于Maxwell-Stefan和Nernst-Planck模型更加严谨，但是这也使模型的求解更加复杂，在模拟电渗析过程时需要预先确定更多相关参数。Nikonenko等[51]通过Kedem-Katchalsky微分方程和边界条件只能得到传递参数解析解，以此研究了电渗析过程对流项对离子通量、浓度分布、电势分布、有效迁移数等的影响。

因为通过实验精确测定模型中所有传递参数难度较大，所以一般忽略对电渗析性能影响较小的参数或者寻找参数间的关联性，根据已有参数估算其他参数以减少自变量个数。Auclair和Larchet等[50,52]提出了Kedem-Katchalsky 方程中传递参数的关系式，以减少方程中独立传递系数。他们在估算离子交换膜水迁移数的研究中发现通过Kedem-Katchalsky 方程并结合膜电导率、扩散渗透率和反离子迁移数计算得到的水迁移数更接近实验数据，并且对溶液浓度的适用范围更广。因此，认为后续对该模型的研究将集中于两方面：一方面是合理简化模型方程；另一方面是借助软件工具对模型进行数值求解，模拟电渗析传递过程。

3.4 模糊逻辑模型

上述理论模型是基于非平衡热力学方程及电化学基础方程推演出来的，这些模型基本能较好地应用于不同离子传递过程或者不同规模的电渗析组器，但是计算往往较为复杂并且还需要如膜性能、扩散系数等详细参数[53]。模糊逻辑推理系统和人工神经网络模型可较好地解决这些问题，适合类似于电渗析这种非线性复杂的过程模拟[54-55]。

模糊逻辑是一种多值逻辑，允许在诸如对/错、是/否、高/低等常规值之间定义中间值，形成数学模型并使用计算机处理，在模拟应用中达到使编程计算更类似于人类思维的目的[56]。Jing 等[57]采用模糊逻辑模型，通过MATLAB 中的自适应神经模糊推理系统预测了电渗析过程浓度、温度、流速和电压对NaCl 溶液分离率的影响，并且分离率预测值与电渗析实验数据之间的相关系数可以达到0.988。该模型对于特定实验得到的预测值和实验结果匹配度很高，但不适用于放大实验或项目，这也是该模型应用较少的主要原因。不过Sadrzadeh 等[58]开发了一种数学模型和模糊逻辑模型耦合的新模型用于预测电渗析法分离污水中锌离子，通过考察不同操作条件并比较模型的预测结果，发现耦合模型计算结果与实验值的相对均方差为0.05，比常规数学模型小很多，并且几乎在所有操作条件下都适用。因此，模糊逻辑模型可以通过和其他常规数学模型耦合，提高该模型的普适性，以应对不同分离体系电渗析过程模拟。

3.5 人工神经网络模型

人工神经网络利用相互联系的数学节点或神经元形成一个可以快速有效模拟复杂函数关系的网络，它能够将输入的数据通过内部计算得到所需的输出值[59-60]。神经网络最基本的组成就是神经元（或叫作节点），每个输入值乘以对应的权重因子，再通过节点的加和计算和传递函数估算最后的输出值。近年来，人工神经网络在微滤[61]、超滤[62]、纳滤[63]、反渗透[64]、气体分离[55]、膜生物反应器[65]等很多膜过程中被用作强大的模拟工具。因此相关研究人员将基于人工神经网络的传质模型应用于电渗析过程。如图4所示，输入值（如电压、流速、温度、浓度）通过多层神经网络转变为预期反馈值（分离率或电流效率），在隐藏层的辅助下可近似得到任一输入-输出映射，以实现预测电渗析性能的目的。

图4 用于电渗析建模的多层人工神经网络结构［66］

Chindapan 等[67]采用人工神经网络模型预测电渗析脱盐过程中鱼露的质量变化情况，并通过遗传算法多目标优化确定适宜的操作条件。Sadrzadeh等[66]应用神经网络模型预测电渗析法去除废水中铅离子的分离效果以及电渗析分离率的非线性行为，模拟结果与实验值的标准偏差不大于1%；并且，对该模型与一般数学模型进行了比较，发现人工神经网络模型在各种不同操作条件下都能比数学模型更准确地预测电渗析分离效果[68]。尽管采用人工神经网络模型得到的预测结果和实际符合程度很高，但由于该模型过多依赖实验数据且较少考虑电渗析组器结构等对分离性能的影响，不便于在连续运行中使用，因此该模型在实际电渗析传质模拟的应用中受到很大限制。

3.6 半经验模型

半经验传质模型一般基于宏观或实验可得的相关性能或经验系数，并结合电渗析组器的几何结构来模拟电渗析过程[69]。它是一种较上述理论模型考虑因素更多、尺度更广的研究方法，从微观的离子传递行为、扩散边界层等到实际的隔板结构、物质平衡及现象学代数方程等，能更准确地描述大规模的工程项目。图5代表一个电渗析膜堆单元的物质流量以及进出口的变化，这些变量或参数通常被用于建立半经验模型[70]。

半经验模型根据代数和微分方程可分为3种。

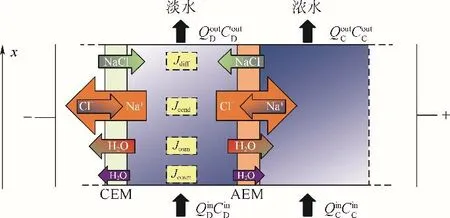
图5 一个电渗析单元隔室和膜间的传递现象［69］

第1种是基于热力学和电化学方程，一般用于计算膜堆电势、电阻及电流等，如式(5)所示。式中，ΔV 表示总电压降，ηnon-Ohm表示非欧姆电压降，rOhm表示欧姆电阻，I表示电流。

第2种是基于质量守恒方程，通过结合质量传递方程以描述流速、离子传递、料液浓度等变化情况，如式(6)～式(8)所示。式中，离子通量Jtot(x)包括欧姆传导通量Jcond(x)和扩散通量Jdiff(x)，t+cem和t-aem表示反离子在离子交换膜中的迁移数，i 表示电流密度，Dcem和Daem表示盐离子扩散系数，hcem和haem表示离子交换膜厚度，CCcem、CDcem、和表示在不同膜-溶液界面处盐浓度。

第3种基于其他经验方程，并考虑相关宏观性能参数，用于计算功率大小、电流效率等[71-74]。

McGovern等[75]基于物质传递、膜电位和边界电位等建立半经验模型，分析盐浓度对电流效率、脱盐率等的影响，从而确定最佳电流密度。Brauns等[76]将半经验模型代入求解程序软件，发现电渗析传质模拟结果与实验结果具有很好的相关性；并且在小试实验中得到的极限电流值在大型电渗析膜堆中试中同样与模拟结果匹配较好，这为电渗析组器的设计和运行提供了重要的理论指导。另外，双极膜电渗析一般多基于宏观的质量守恒、欧姆电阻、离子迁移数等建立数学模型。Koter 等[77]根据离子迁移数、水电渗透系数、离子扩散系数模拟计算双极膜制酸碱的电流效率并确定膜选择性、解离常数等对其的影响规律。总的来说，半经验模型综合了流体动力学、物质传递、质量守恒等不同理论方程，而且适用范围广，有效解决了不同规模层次的计算模拟问题。

4 结语与展望

电渗析过程传质模型化研究为电渗析结构设计和操作工艺优化提供理论指导，从而有助于导向性提高电渗析的分离能效。因此，提高传质模型的准确性和普适性是促进电渗析技术进一步发展的关键所在。本文总结了电渗析过程传质模型的研究现状，并分析了各模型的应用优势及限制因素。根据目前的研究成果，Maxwell-Stefan 模型（特别对于多溶质溶液体系）和Kedem-Katchalsky模型因求解复杂而较少应用于电渗析传质模拟中，模糊逻辑模型和人工神经网络模型因过多依赖实验数据而无法在大规模电渗析分离系统中应用。相比之下，Nernst-Planck 模型和半经验模型更易与其他相关方程联立耦合，使模拟结果更符合实际传递行为，这也将成为后续传质模型的研究重点。今后电渗析传质模型潜在的研究方向主要有：

（1）进一步优化电渗析传质模型（特别是Nernst-Planck 模型和半经验模型），提高模拟结果的准确性，进而可深入系统研究膜性能及工艺参数对电渗析传质的影响规律，在实际应用中确定适宜的离子交换膜和高效分离的操作策略；

（2）结合数值求解和仿真软件（MATLAB、Comsol、TK-solver 等），对电渗析传质进行过程模拟和计算仿真，更直观、准确地描述电渗析过程中物质的传递行为，为探究电渗析分离过程物质传递机理、溶液各组分间的相互影响机制等提供有效途径；

（3）模拟双极膜电渗析、反向电渗析以及与其他技术（风能、太阳能等）耦合的电渗析过程，并且量化地评价电渗析工艺经济性；

（4）基于实际分离体系的相关传质系数建立数学模型，提高模型的普适性，使其可预测电渗析在海水淡化、物料脱盐、废水处理等多领域应用中的传质行为及分离效果。