有效追问 让数学课堂更精彩

胡长伦

(重庆市江津区杜市学校 重庆江津 402272)

追问，就是追根究底地问，即在学生回答教师提出的问题后，正确的追因，不对的追错，肤浅的追根。教师通过追问，引导学生准确把握思维的方向，并及时启发和激发学生的思维，促进其进行深入探究，从而提高学生的学习能力。课堂中的追问既是一门学问，更是一门艺术[1]，是教师教学智慧和教学艺术的体现。恰当的追问能让课堂成为智慧的天堂。

一、在出现错误之处追问，纠正思维误差

学生受知识、经验和方法的局限，在学习过程中出现一些错误是正常的[2]。老师要因势利导,及时追问错误的原因，引导学生从错中求知，从错中探究，让学生自己发现错误，推翻错误，得出符合逻辑的结论，从而使学生的认识更为深刻。

案例：在轴对称的新课教学中，学生对轴对称的概念比较模糊。

师：平行四边形是轴对称图形吗？

生：是。

师：它的对称轴是什么？

有的学生回答“对角线所在直线”，也有人回答“对边中点所在直线”。

师：为什么会有两种不同的结果？

教室里响起一片争论声。

师：你能通过折纸来证明吗？

学生们通过画平行四边形，并剪下来，折叠，发现无论沿哪条直线，两部分均不能完全重合。通过动手操作，学生再次深刻感悟了轴对称图形的本质特征：一个平面图形沿某一直线对折，两部分能完全重合，而不是对称轴两边的图形大小相等。

在平时的教学中，学生回答问题出错时，教师要耐心倾听，将这种错误作为资源加以利用，挖掘错误的闪光点，给予及时、准确、客观的点评，让学生明白为什么会出错，后面碰到此类问题时要注意些什么，将学生的想法从朦胧状态引向清晰。

二、在缺乏深度之处追问，引发深层思考

在课堂教学中，学生对问题的回答往往停留在表面上，甚至是盲目猜题或想当然地进行回答。此时，教师可针对学生的回答进行更深层次的追问，引导学生深入探讨问题思考的方向，培养学生分析问题的能力。

追问1:这种方法你是怎么想到的？

追问2:你这样做的目的是什么？

追问3:你这样做的依据是什么？

追问4:满足哪种特征的方程可以用这种方法？

教师通过追问能促使学生进行总结，使其养成良好的总结习惯，让学生对数学活动中涉及的知识、思想方法、思路进行总结，对解题的策略进行优化和重组，从而加深其对问题的理解，提高学生分析问题和解决问题的能力。

三、在产生困惑之处追问，实现释疑解惑

在教学过程中，教师要根据课堂的情况，在学生产生困惑之处追问，紧扣问题不放，将问题引向深处，解决学生的困惑。这也是提高课堂效率的有效途径。

案例：如图，△ABC中，∠CAB=∠CBA＝45°，CA=CB,点E为BC的中点,CN⊥AE交AB于N。求证：AE=CN+EN。

在外理线段和差问题时，学生常考虑截长补短,有的同学在AE上截取AF＝CN， 连接CF,通过证明△ACE≌△CBF、△BEN≌△CEF，最终证明了AE=CN+EN。有的同学在EA上截取EF＝EN，连接CF，但无论如何证明不到△BEN≌△CEF（图1），因而陷入困惑之中。还有同学延长CN至F，使NF=EN，连接BF，也陷入了证明不了△BFN≌△BEN（图2）的困惑，从而进入误区，没办法往下做了。此时，教师追问1：截长补短的目的是什么？

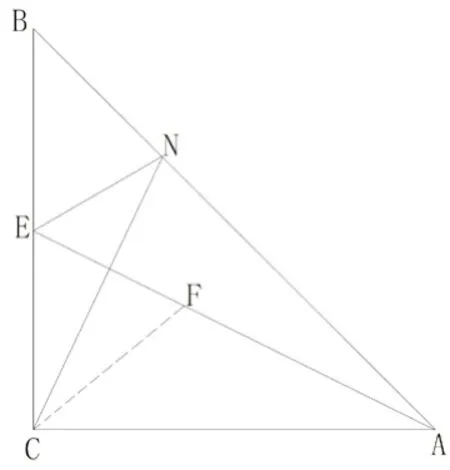
图1

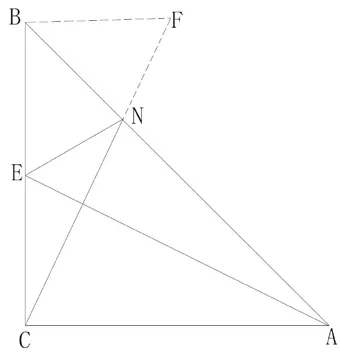
图2

追问2：为什么照上述方法截长补短行不通？

追问3：∠BCN和∠EAC有什么样的关系，它们位于哪两个三角形中？这两个三角形有一条边相等了（AC=BC），又有这对角等，通过添加辅助线满足角等或者边等，是否就能得到全等了？

有的学生作∠ACF＝45°交AE于F；有的作∠ABC的平分线交AE于F；有的延长CN至F，使CF＝AE；有的作BF⊥BC交CN的延长线于F……

教师可通过追问对学生的思维进行即时疏导、点拨，把学生引向问题的关键处：无论是截长还是补短，都是要将几条线段的和差问题转化为证明两条线段相等的问题，而这一般都要通过构造出全等三角形来解决。

四、在发生意外之处追问，演绎独特价值

案例：下面是一位教师上“一元一次方程——去括号”时的一个教学片断：

师：如何解方程3（x－1）＝－6(x－1)？

生1：老师，此题有问题，3不可能等于－6。

老师瞄了他一眼。

生2：老师，我还没有开始计算，就已看出来了，x＝1！

师：光看不行，要按要求算出来，才算对。

生3：先两边同时除以3，再……（被老师打断了）

师：你的想法是对的，但以后要注意，刚学新知识时，记住一定要按课本的格式和要求来解，这样才能打好基础……

课堂教学随时会发生意外。然而，这位老师仅仅把它看成教学过程中的“节外生枝”，对生1熟视无睹，对生2、生3草率了断。这就在无形中束缚了学生的创造性思维。教师要大胆打破预设的框架，对学生的意外回答，要给予积极的回应，以睿智的追问（生1回答后，追问：有什么样的问题？可以同时除以（x－1）吗？方程两边同除以一个数时要注意什么？对生2、生3追问：你是怎样得出答案的？你是怎样想到的？这样做有什么好处。追问后，老师可在方程右边+1，再让学生解方程，就自然过渡到去括号解一元一次方程了）激活学生思维，拓展其想象空间，让教学中的“节外生枝”演绎出独特的价值。

有价值的追问能够让学生在发生认知错误时及时修改，能够在学生理解重难点时豁然开朗，也能够让不同层次的学生，在对知识点理解参差不齐时查漏补缺。追问的价值在于掌握学生的思维状态，促进其思维能力的提升，同时也促进其表达能力的提升。追问让我们的数学课堂更加精彩，也使我们的教学效果更好。