提升学生数学学科核心素养：问题解决的视角

王海伴

[摘  要] 通过主题“关于导函数零点无法直接求解”的解决，阐述在高考二轮备考复习中，以函数的零点、方程的根、不等式的解集之间的关系为突破口，寻求解决问题的思路与方法，领悟这类数学问题的本质，来尝试激活备考状态下的数学课堂，落实高三学生数学学科核心素养.

[关键词] 数学学科核心素养;导函数;零点

高中数学学科六大核心素养之间相互影响、相互制约、相互促进，其中直观想象是逻辑推理、数学抽象、数学建模的思维基础. 导函数零点无法直接求解，是学生导数应用问题中最常见、最犯难的一类问题，导致很多学生无法参与课堂教学，更談不上核心素养的落实. 下面通过实例来谈谈这类问题中提升学生数学学科核心素养的看法，不当之处，恳请批评指正.

问题提出

在高三文科二轮备考复习中，学生反馈，近几年高考文科数学新课标（Ⅱ）卷导数压轴题，难度较大，得分率很低，通过与学生的交流发现，问题的焦点在于导函数零点无法直接求解，其实2016年20题、2017年21题与2010年新课标理科21题相似.

问题：（2010年新课标全国Ⅱ卷理第21题）设函数f（x）=ex-1-x-ax2.

（Ⅰ）略;（Ⅱ）若当x≥0时，f（x）≥0，求a的取值范围.

问题分析与解决

对于上述问题第二问，笔者在教学实践中，发现部分学生存在以下学习障碍.

学习障碍一：不明白为什么要对原函数求导数，从而导致导函数零点无法直接求解时迷失方向;

学习障碍二：学生对函数的零点、方程的根、不等式的解集之间的关系认识不够，导致无法处理导函数零点问题;

学习障碍三：学生没有从数与形的角度来深刻领悟常见不等式模型，也就谈不上常见不等式放缩模型的应用.

1. 数形结合，尝试求根，落实直观想象素养

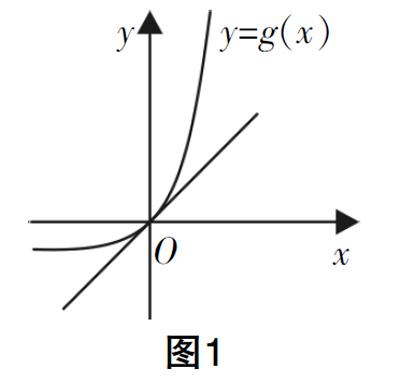
学生完成f ′（x）=ex-1-2ax，x≥0的计算，令f ′（x）=0，无法直接求出f ′（x）的零点，此时引导学生回顾解方程与不等式的常用方法，让其认识到除了从数的角度，也可以从形的角度（图像）近似估算方程的根.通过学生容易理解的方程，例如x2-4=0，由特殊到一般归纳解方程、解不等式、求函数零点的数学本质相同. f（x）=0，即ex-2ax-1=0，从而ex-1=2ax，令g（x）=ex-1，h（x）=2ax，此时类比x2=4的图像解法. 如图1，由于在点（0，0）处g（x）的切线为y=x，所以当2a≤1，即a≤ 时，g（x）>h（x），？坌x∈（0，+∞），则（0，+∞）为f（x）的一个单调递增区间. 又f（0）=0，所以x∈[0，+∞），f（x）≥0.

当a> 时，如图2所示，存在x ∈（0，+∞），使得f ′（x）=0，这样在区间（0，x ）上f′（x）<0，从而（0，+∞）为f（x）的一个单调递减区间. 又f（0）=0，于是当x∈（0，x ）时，f（x）<0. 综上a∈-∞， .

通过问题解决可以看出，当x≥0时，要使f（x）≥0，只需f（x）min≥0，但方程f ′（x）=0无法直接求出，学生思维受阻，无法通过导函数判断函数的单调性. 引导学生回顾高中阶段解方程的一般性思路，不能直接解方程时，能否考虑利用图像法近似解方程，考虑在点（0，0）处g（x）的切线为y=x，对2a进行分类讨论，使问题得到了顺利解决. 通过数形结合，使学生在求根的思考中有效落实了直观想象素养.

2. 参考特值，多次求导，提升逻辑推理素养

引导学生再次类比x2-4=0的图像解法，令f ′（x）=0，无法直接求出f ′（x）的零点，然而导函数f ′（x）的单调性未知，怎样考察y=f ′（x）的单调性，此时自然会想到计算f ″（x）. 设g（x）=ex-2ax-1，g′（x）=ex-2a，当a≤ 时，g′（x）≥0，这样[0，+∞）为g（x）的一个单调递增区间，于是g（x）≥g（0），即f ′（x）≥0，从而[0，+∞）为f（x）一个单调递增区间，f（0）=0，则x∈[0，+∞），f（x）≥0. a∈ ，+∞时，由g′（x）>0，得ex>2a，解得x>ln（2a），所以[0，ln（2a））为g（x）的一个单调递减区间，[ln（2a），+∞）为g（x）的一个单调递增区间. 又g（x）min=g（ln（2a））

方程f ′（x）=0无法直接求出，是问题解决的重要障碍，此时学生往往会出现思维受阻. 此时，教师应该减慢课堂节奏，再次类比x2-4=0的图像解法，进一步引导学生体会再次求导函数的必要性，让学生明白两种解法的本质是相同的，都是以利用图像法解方程、解不等式作为出发点. 此外，我们可将参数a分离，构建函数h（x）= ，“参考特值，多次求导”，最后借助洛必达法则，问题得以顺利解决. 这样在透视数学问题的本质中提升了学生逻辑推理素养.

3. 构建直观模型，适当放缩，发展数学建模素养

直观模型的建立，需要教师通过辅助教学工具，引导学生通过感知形、理解数的角度来学习，增强学生对模型的深刻理解，例如对于ex≥1+x的理解，这样才有可能将这一直观模型在问题解决中信手拈来. 由不等式模型ex≥1+x，得f ′（x）≥x-2ax=（1-2a）x，即a≤ 时，f ′（x）≥0 （x≥0），故（0，+∞）为f（x）的一个单调递增，而f（0）=0，于是当x≥0时，f（x）≥0. 由ex>1+x（x≠0），得e-x>1-x（x≠0）. 当a∈ ，+∞， f ′（x）

学生在求f（x）在[0，+∞）上的最小值时，发现方程f′（x）=0无法直接求出，思维受阻，教师引导学生，从数与形的角度认识ex≥1+x，x≥ln（x+1）等模型，引导学生利用不等式ex≥1+x（当且仅当x=0时，取等号）直观模型，参考特值f（0）=0，f′（0）=0，使問题得到圆满解决，从而有效发展了学生逻辑推理与数学建模素养.

4. 设出零点，整体代换，增强数学运算核心素养

学生核心素养的提升，不能定格在简单模仿解决问题的层面上，而是要抓住数学本真. 教师应该在把握学情、注重过程性学习的基础上，努力为学生设置合理的问题.充分调动学生的积极性，让其创造性地解决问题，这也正是数学的魅力所在.

例：（2013年新课标全国Ⅱ卷理第21题）已知函数f（x）=ex-ln（x+m）.

（Ⅰ）略;

（Ⅱ）当m≤2时，证明：f（x）>0.

引导学生完成，当m≤2，x∈（-m，+∞）时，ln（x+m）≤ln（x+2）的判断，为后续问题扫清障碍. 故只需证明当m=2时，f（x）>0. 当m=2时，函数f ′（x）=ex- 在（-2，+∞）上单调递增. y=f ′（x）导函数零点无法直接求解，给学生充分探究空间，为创造性解决问题奠定基础. 又f ′（-1）<0，f ′（0）>0，故f ′（x）=0在（-2，+∞）上有唯一实根x0，x0∈（-1，0）. 当x∈（-2，x0）时，f ′（x）<0;当x∈（x0，+∞）时，f ′（x）>0，从而当x=x0时，f（x）取得最小值. 此时根据学生探索情况，注意引导学生体会转化思想的重要作用，然后通过f ′（x0）=0得出ex0= ，这样就得到ln（x0+2）=-x0，而f（x0）= +x0= >0. 由以上分析得m≤2时，f（x）>0.

通过问题解决，学生领悟到当导函数零点直接不可求时，可以借助零点定理设出零点，由f ′（x0）=0，得ex0= 进行整体代换，从而使问题得到顺利解决，有效促进了学生逻辑推理与数学运算.

结束语

要论证某种教学方式的正确性和有效性，应该根据核心素养的要求进行.检验学生核心素养的高低，必须通过解决数学问题来体现. 问题解决过程能有效增进学生数学素养的落实. 在教学实践中，只要教师慢下匆忙的脚步，进行主题梳理，抓住数学问题本真，充分进行形与数的有机结合，即使在高三二轮复习的课堂教学中，学生也能领略沿途美丽的风景，这样就自然将数学学科素养落到了实处.