On the plastic buckling of curved carbon nanotubes

Mohammad Malikan*

Department of Mechanical Engineering, Faculty of Engineering, Islamic Azad University, Mashhad Branch, Mashhad, Iran

Keywords:Plastic buckling Curved carbon nanotubes Nonlocal strain gradient theory Euler-Bernoulli beam Rayleigh-Ritz method

ABSTRACT This research, for the first time, predicts theoretically static stability response of a curved carbon nanotube (CCNT) under an elastoplastic behavior with several boundary conditions. The CCNT is exposed to axial compressive loads. The equilibrium equations are extracted regarding the Euler-Bernoulli displacement field by means of the principle of minimizing total potential energy.The elastoplastic stress-strain is concerned with Ramberg-Osgood law on the basis of deformation and flow theories of plasticity. To seize the nano-mechanical behavior of the CCNT, the nonlocal strain gradient elasticity theory is taken into account. The obtained differential equations are solved using the Rayleigh-Ritz method based on a new admissible shape function which is able to analyze stability problems. To authorize the solution, some comparisons are illustrated which show a very good agreement with the published works. Conclusively, the best findings confirm that a plastic analysis is crucial in predicting the mechanical strength of CCNTs.

A decade ago, an ever-increasing trend has been witnessed in the application of the mechanics of plastic deformation of structures in different engineering discussions and industrial processes [1]. Indeed, it has been generalized that engineering materials should not be analyzed and designed only in a perfect elastic situation. In reality, most of the structures enter into the plastic region due to unpredictable conditions such as high temperatures, high loads and mistake manufacturing leading to distortion. In the analysis of distorted (non-straight, twisted or bent) nanomaterials, it is important to take into consideration the plastic deformation in the material behavior. As a matter of fact, a deformed material with a steady deformation exceeds the elastoplastic and plastic regions.

Among the nanostructures, carbon nanotubes (CNTs) play a significant role in the reinforcement of nanocomposite structures [2]. Thus, in order to develop CNT-based composite materials, an exact knowledge of the CNTs' mechanical deformation is required crucially. Obviously, some nanotubes do not retain their initial regularity when using, and they distort. These abnormalities may occur during the manufacturing process or after that as a result of the matrix effect. Accordingly, the modeling of this type of nanostructure, in the form of a shell or beam without curvature, may involve a significant error with the results. Some researchers have analyzed mechanically the CNTs with an initial curvature in a perfect elastic condition (temporary curvature) [3-13]. Some researchers, on the other hand, have generally studied the elastoplastic mechanical behavior of various materials [14-27]. Whereas studies on the mechanics of plastic of CNTs are very limited and have resulted in a few studies [28-30].

Dealing with the literature, there are hitherto no publications on the elastoplastic stability of curved carbon nanotubes(CCNTs). Thus, this paper aims to fill such the gap. In this paper,it is assumed that the CNT involves an initial stable curvature and such an irregularity may bring the material into an elastoplastic region and beyond. CNTs typically fail at 6% strain in light of structural defects [28]. Therefore, the material can be predictably in an elastoplastic behavior if the curvature value in a CNT goes up as high as the material fail. To model the CCNT mathematically, the Euler-Bernoulli beam model is used in the energy method via a generalized variational principle by employing nonlinear Lagrangian strains. In order to investigate small-scale effects, nonlocal strain gradient theory is taken into account which involves microstructural size-dependent effects and a second stress gradient factor. To solve the mathematical relation of buckling, the Rayleigh-Ritz solution method is applied. This method is adopted based on a new shape function by which the critical buckling load can be calculated for several boundary conditions, in particular, free edges. Thereafter, numerical results are sketched graphically by variation in the fundamental and key criteria.

Figure 1 demonstrates schematically a CCNT in a rectangular coordinate system for both two-dimensional and three-dimensional pictures. The geometrical symbols are respectively,uniform thickness (h), exterior radius (R), internal radius (r), and length of the tube (L) and also the size of curvature (e).

The curved geometry of the CCNT can be formulated mathematically as below (Fig. 1(a)) [13]

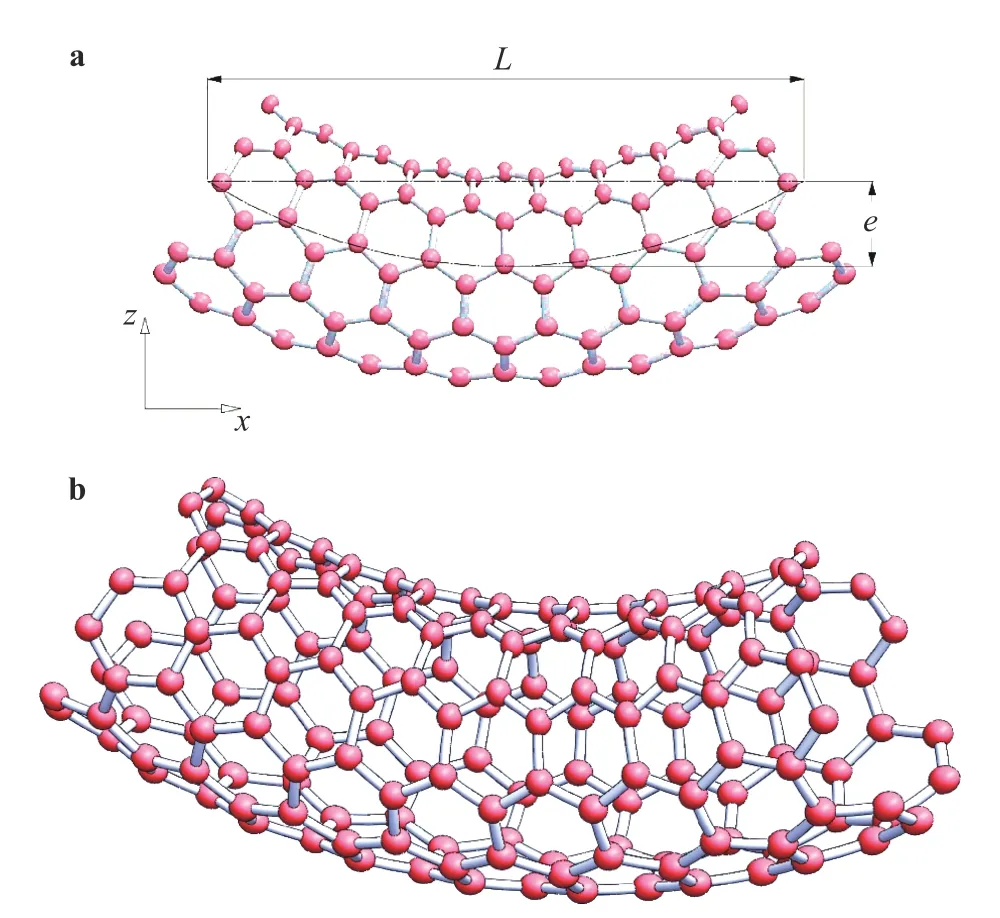
Fig. 1. a Two-dimensional and b three-dimensional models of the curved carbon nanotube (e shows the curvature and L depicts the length of the curved nanotube).

To define plasticity behavior, there are two plasticity theories, i.e. deformation theory of plasticity (DTP) and flow theory of plasticity (FTP) [20, 21]. The deformation or total stress theory of plasticity described total strains related to the total stresses and no stress history effects exist. This theory applies to problems with proportional loading. On the other hand, in the flow theory,there is a possibility to decompose the total strain of material in a sum or multiplication of an elastic and a plastic section. In fact,the material before the plastic area also has a linear elastic range. The elastic strain section can be calculated through linear or hyperelastic models. However, to determine the strain of the plastic section, a flow law and a hardening model should be used. In FTP, the stress increments are related to the stress ones which mean the stress history effects exist. Undoubtedly, this concept is more general and applicable than DTP.

DTP containing constitutive equation of Hencky as

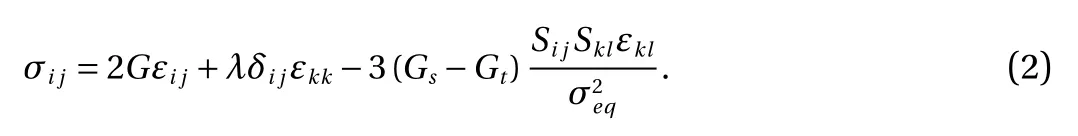
FTP involving constitutive equation of Prandtl-Reuss as

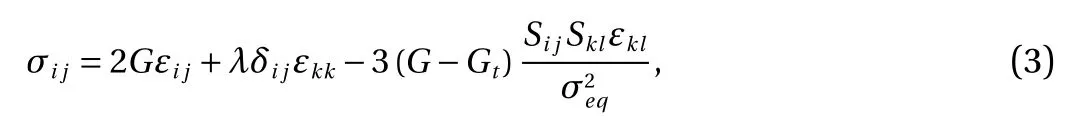
in which Sijdenotes components of the stress deviator, Gtrepresents the tangent shear modulus, and Lamè (Gs, λs) and elastic (G, λ) coefficients. Furthermore, σeqdepicts an equivalent stress factor with the assumption that the material follows the yield criterion of von Mises as below

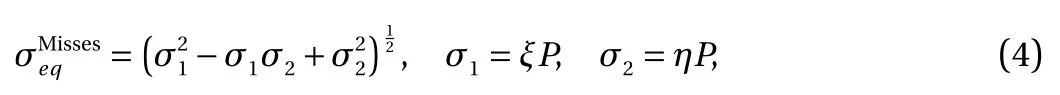
in which the σ1and σ2are the stress on the edges for a plate along x- and y-axes, and the values of η and ξ determine the type of loading. In this paper, the values are 0 and 1 respectively, for a CCNT under axial compression.

The in-plane stress-strain constitutive equation can be defined as

where

The parameters in Eq. (6) are

in Eqs. (5) and (6), E and Etare the Young's and Tangent elasticity moduli, respectively, αxxis the instantaneous moduli.This modulus depends on the theory of plasticity by which the material behavior can be modeled. Moreover, in FTP, the elastic components are as

In DTP, secant values are assumed for Young's and shear moduli as

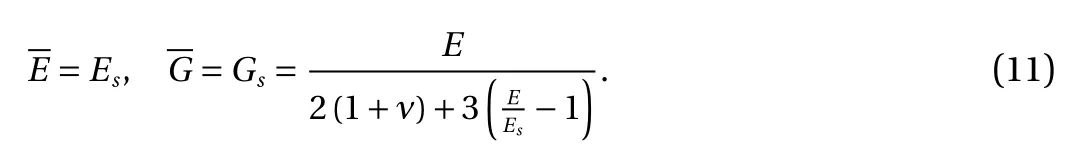
This research adopts the Ramberg-Osgood elastoplastic relation in the form [31]

where k and n describe the status of the elastoplastic curve of the stress-strain diagram and σ0shows nominally the yield stress.Note that when n, k→∞ the model is in a fully plastic behavior and when n, k→0 the material behavior of the model is perfectly elastic. In the Ramberg-Osgood hypothesis, the secant elasticity modulus (Es) and the tangent one (Et) can be indicated as below

The kinematic model is here operated in the framework of the Euler-Bernoulli beam approach as [32, 33]

The components w(x) and u(x) introduce the kinematic of the mid-plane points and u1(x, z) and u3(x, z) are the kinematic of the domain along x- and z-axes. In addition, a thickness coordinate is symbolized with z.

The following expression obtained from Eq. (15) is the nonlinear axial component of Lagrangian strain on the basis of the strain-displacement of von Kármán for the CCNT

The resultants which describe the axial and moment stresses in the CCNT can be used by means of the following relations

where Nxand Mxrepresent the moment and axial stress resultants, respectively. Hence, based on the Eqs. (5) and (17),we obtain

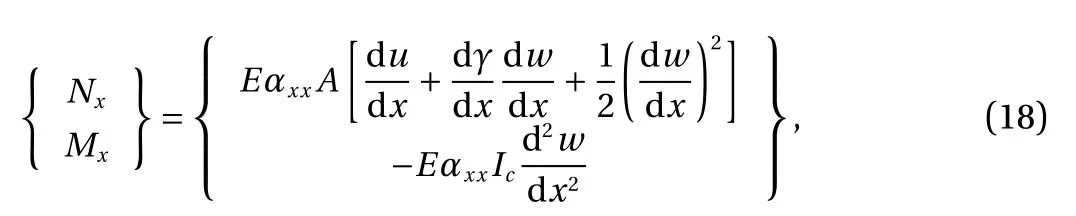
where Ic= π(R4-r4)/4 represents the moment of area of the cross section and also A indicates the cross-section area of the CCNT.

To determine the effect of tension which is because of curvature in the CCNT, the following process would be done

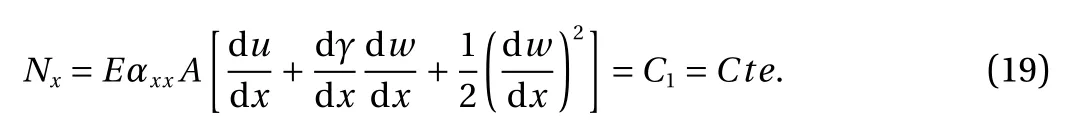
Integrating Eq. (19) would calculate the parameter C1as

in which C2defines a constant of integration. Afterwards,applying u (0)=u(L)=0 on the Eq. (20), we have

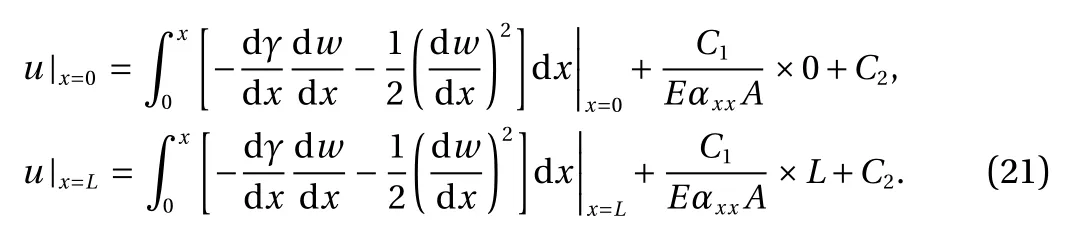
Rearrangement gives

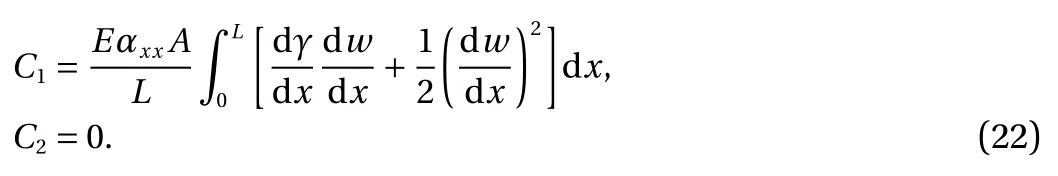
The generalized variational principle is here invoked to seek the equilibrium state as

in which δ means variation δW and δU are work done by external objects and virtual strain energy (This paper ignores the effects external objects, e.g. foundation), respectively. The variation of strain energy can be presented as

Imposing δΠ = 0, the equation of the equilibrium state for a CCNT can be obtained as

Among the theories which probe the effects of size into a micro/nanoscale schema, the nonlocal strain gradient theory (NSGT) has been widely employed by which the influences of the microstructural size dependency and nonlocality can be got as below [34]

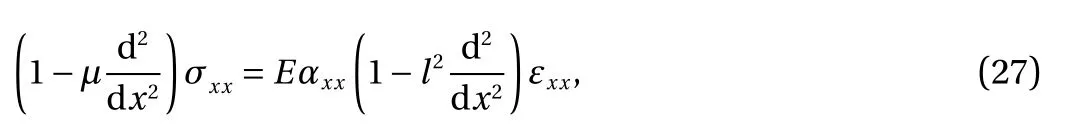
where l displays a length scale coefficient and μ is a nonlocal parameter that is equal to (e0a)2. Moreover, e0shows a physical constant and a = 0.142 nm is the bond length of carbon-carbon atoms. It is worth mentioning that the nonlocal parameter and the length scale coefficient should possess variable values and cannot be constant. As a matter of fact, such factors depend on the various conditions, for example, different boundary conditions. In order to have reasonable values for the smallscale parameters, some experiment tests or molecular mechanics analysis can help [35, 36].

In the following, by applying Eq. (27) into Eq. (18), the moment stress resultant can be rewritten as below [37-45]

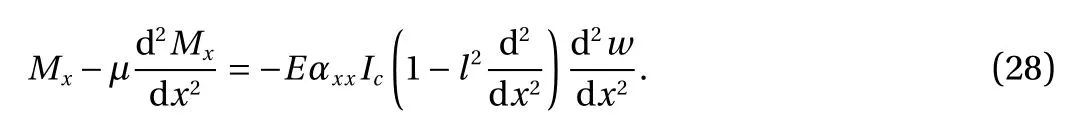
Based on substituting Eq. (28) into Eq. (26), we get

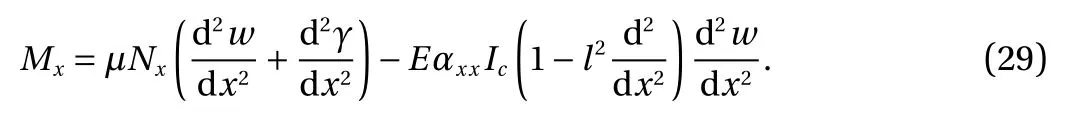
Here, as a result of prebuckling compressive axial forces, we have

Then, by inserting Eqs. (22), (29), and (30) into Eq. (26), the following relation can be achieved which is the elastoplastic buckling relation of a CCNT

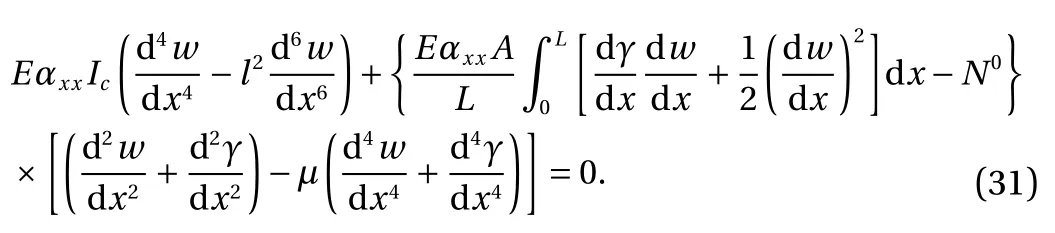
In order to solve the eigenvalue problems, the Rayleigh-Ritz solution technique can be a good choice [46-49] owing to its capability to give high accurate numerical outcomes. The method is a semi-analytical one and satisfies eigenvalue problems,many of which should be solved linearly for which the numerical solutions can be employed. However, such numerical methods have larger solution time [50-53] and cannot be cost-effective. Hence, semi-analytical methods can be a better suggestion to solve eigenvalue problems. The transverse displacement in the Rayleigh-Ritz method was presented as [49]

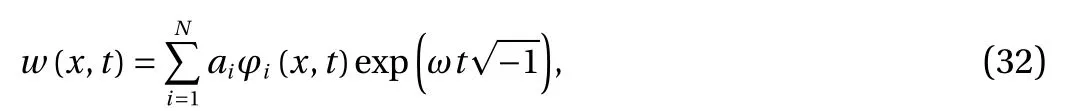
in which φi(x,t) is fundamental mode shapes and ω is natural frequency in vibrational analyses based on time, airepresents the unknown variable which should be calculated

The only difficult thing in the semi-analytical solution methods, like the Rayleigh-Ritz one, might be determining mode shapes which should satisfy boundary conditions. In this research, a new mode shape is assumed by which a very good agreement has been obtained when comparing the numerical outcomes with Refs. [46-49]. The mode shape determining several boundary conditions is innovatively derived as below

in which λ and ζ define several boundary conditions as shown by Table 1.

The conditions mentioned in Table 1 can satisfy the essential boundary conditions given in Table 2.

To use the semi-analytical polynomial methods like the Rayleigh-Ritz one, first, the convergence rate of the solution method should be investigated. To this, Fig. 2 is presented with which it is observed that a suitable rate for convergence of the solution can be chosen as N = 5. By choosing this, the numerical outcomes would be acquired correctly. Moreover, due to solving a symmetrical problem and being the beam an isotropic one,naturally, the behavior of the SC should be as same as the CS boundary conditions. Note that this claim can be right for CF and FC boundaries.

The numerical results and the related discussion would bebegun with the formulation's validation. To do this, according to Tables 3-6 taken from Refs. [54, 55], the critical elastic buckling load of a nanobeam is evaluated whilst the elasticity properties were chosen as E = 1 TPa, υ = 0.19, and diameter of the beam was selected as d= 1 nm. The numerical results within the Tables are for Euler-Bernoulli beam equation solved with an explicit analytical solution [54] and the differential transform method(DTM) [55]. As it is found, in the three cases (µ = 0 nm2, µ = 1 nm2, and µ = 2 nm2), the results of the references and the present work are close to each other and reveal an excellent agreement into clamped-clamped (CC), hinged-hinged (HH) and clampedfree (CF) boundary conditions. Although the results of CH boundary conditions are slightly farther from the literature, it can be acceptable. These Tables approve the efficiency and accuracy of the present admissible function for various boundary conditions.

Table 1 Admissible quantities for several boundary conditions

Table 2 Essential boundary conditions

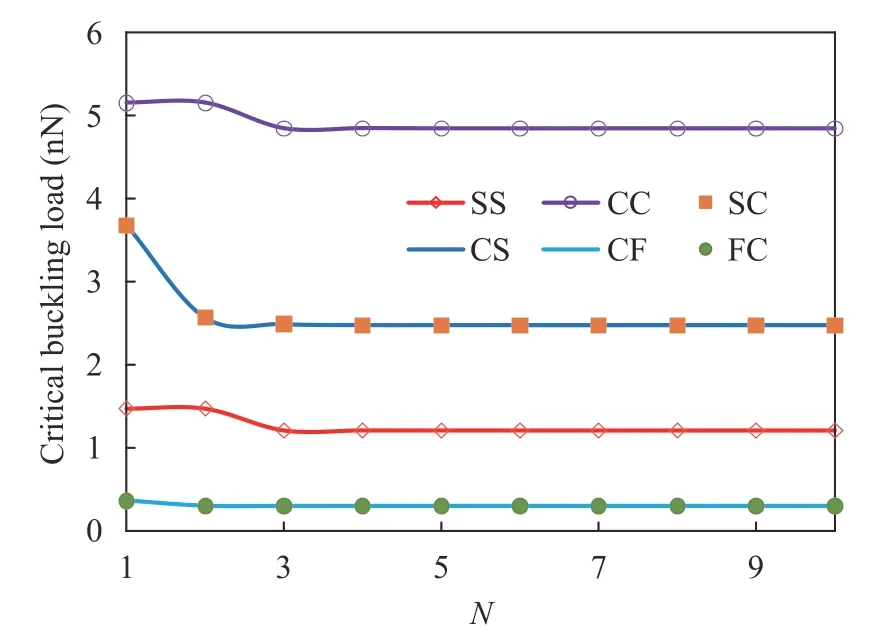
Fig. 2. Convergence rate of the Rayleigh-Ritz results for different boundary conditions for a straight single-walled carbon nanotube (l= 0, e0a = 0, L = 20d, E = 1 TPa, ν = 0.19, d = 1 nm).

In addition to the above validation of the present solution's shape function, we can use Ref. [56] in which some admissible functions were employed (Table 7) which had appropriate results. As can be seen, Fig. 3 shows an excellent agreementbetween the results of the present admissible function with those obtained from Ref. [56]. The superiority of the present admissible function versus those mentioned in Table 7 can be the possibility of applying free edges and also simpler utilization and application.

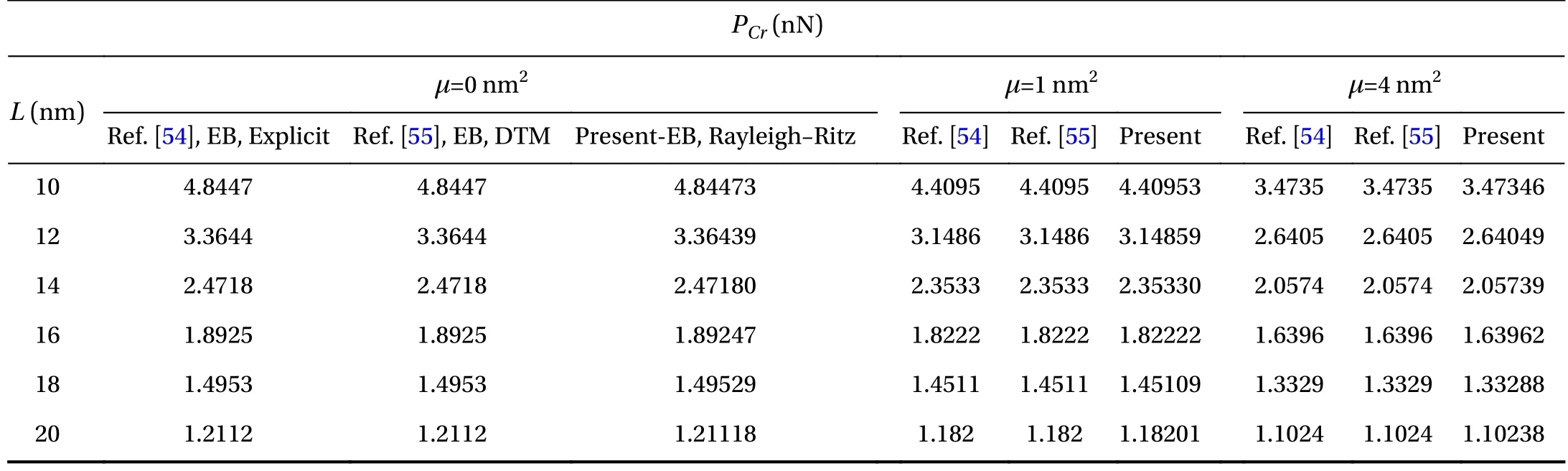
Table 3 Comparison of elastic critical loads originated from literature for a HH beam

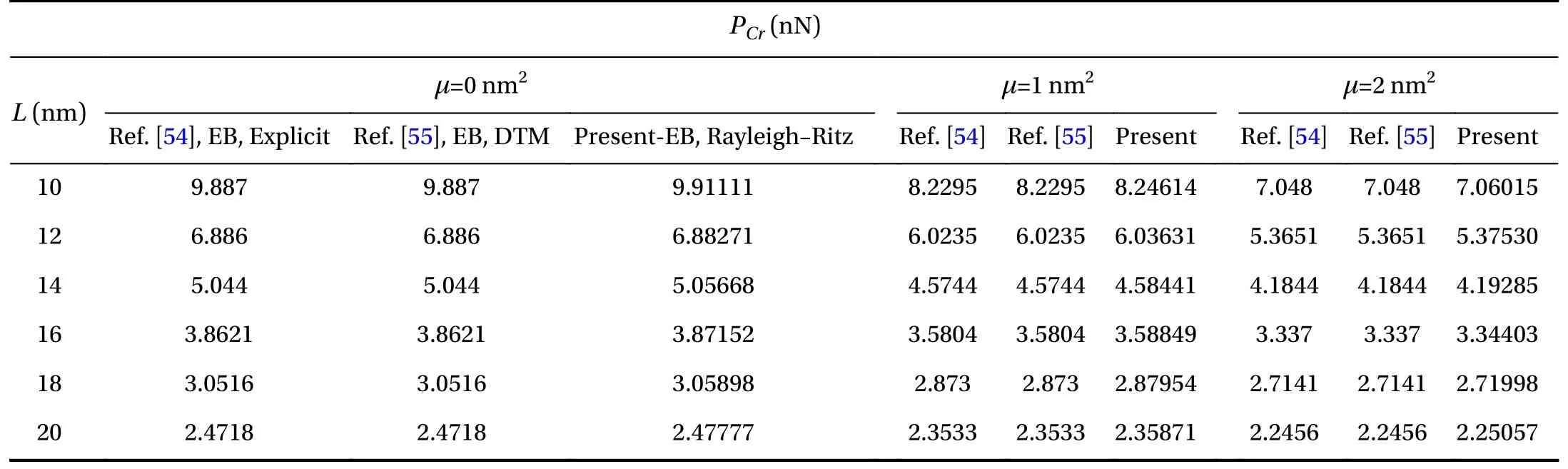
Table 4 Comparison of elastic critical loads originated from literature for a CH beam.

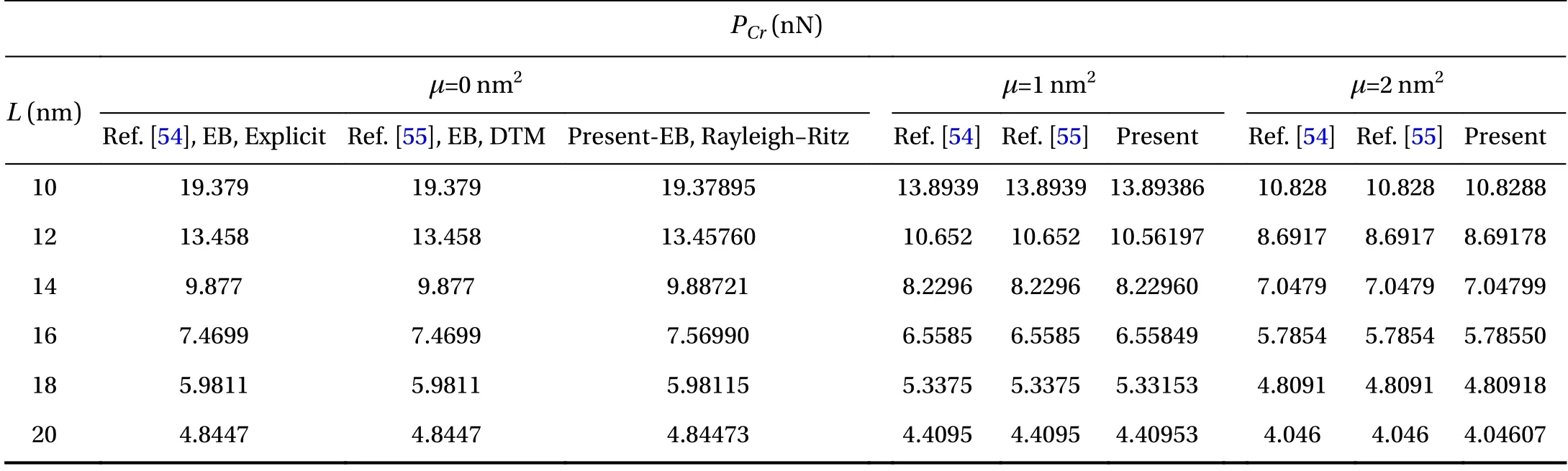
Table 5 Comparison of elastic critical loads originated from literature for a CC beam.

Table 6 Comparison of elastic critical loads originated from literature for a CF beam.

In generating the numerical outcomes, the CCNT is analyzed by the mechanical properties [56-66], 0.5 nm ＜ e0a ＜ 0.8 nm [57], 0 ＜ e0a ≤ 2 nm [35, 58], E = 1000 GPa, ν = 0.19, h = 3.4 Å,R = 5 Å.

The critical load of elastoplastic buckling is given in terms of different variables. It is necessary to affirm that in this study, according to the elastoplastic analysis, it is assumed that the nanotube because of the curvature is at the point of material yielding (i.e., the maximum stress is equal to the yield stress). So, the Ramberg-Osgood curve is in the elastoplastic state, but not in the elastic-perfectly plastic (n = ∞). For this purpose, Fig. 4(a)and (b) shows the critical elastic load beside the critical plastic load for two theories of flow and deformation with the smallscale parameters variations. In the first figure, the boundaries of the nanotube are modeled as the pivot condition, and the Ramberg-Osgood parameters are also chosen in the assumed sizes. It is evident from the figure that increasing the strain gradient parameter leads to an increase in the critical load of plastic.However, the critical load of nanotube in the elastic region is far more than its value in the yield point. In fact, the yielded material will be less stable. It is interesting to note that the amount of the critical plastic load obtained for the theory of flow is more than the theory of deformation. The second figure, on the other hand, has plotted the effects of the nonlocality parameter with the same values of the other parameters as in the previous figure. The increase of the nonlocal parameter decreases the critical load of the plastic. The two figures prove that the nonlocality and the effect of size in plastic conditions, as same as the elastic conditions, give the nanotube the effects of stiffness-softeningand stiffness-hardening, respectively.

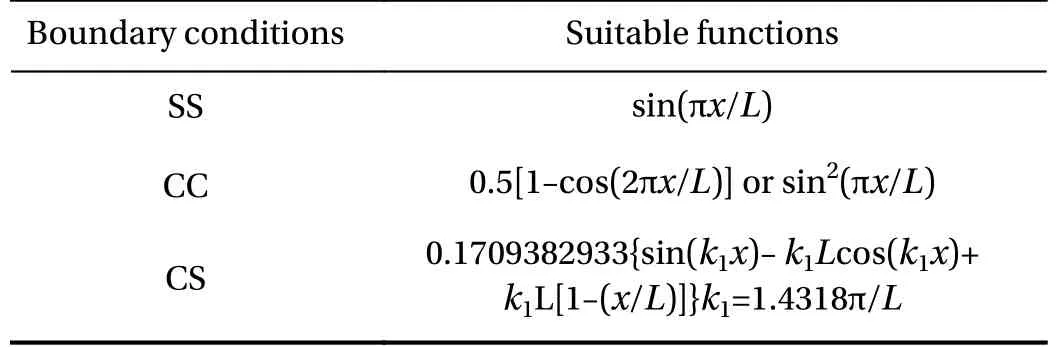
Table 7 Admissible functions

In order to investigate the elastoplastic state for both the theory of flow and plastic deformation, Fig. 5 is presented with the results of several boundary conditions. In fact, the path to this figure is a complete elastic state to the plastic regime. The yield stress to the current stress ratio is considered to be from 0.2 to 2.It is quite clear that the nanotube has a much lower resistivity in the case of the yield point in contrast to elasticity case. Additionally, the clamped boundary condition has a much higher critical load than the hinge and free edges. It should be noted that the plastic buckling will occur in two states: in the first case, the material will first be loaded and the load will be increased gradually so much that the material is yielded due to the plastic buckling load. In this case, an elastic buckling will first occur and if we remove the load, the material is completely reversible to its original state before deformation. But if we hold the load and raise it,we will reach the yield point. Naturally, in this case, the critical load of plastic should be greater than the critical load of elastic of the material. To analyze this plastic buckling model, relationships should be in the post-plastic buckling state. The second manner of plastic buckling is a condition where the material is yielded for a variety of reasons (high temperature, bending, distortion, etc.), or is in an elastoplastic state, and loaded onto it to calculate its stability. Logically, in this case, the critical load of plastic should be less than the critical elastic load of the material.This study investigates this plastic stability state of the nanotube which is in the yield point because of the distortion and irreversible curvature due to wrong manufacturing. Figure 5 represents explicitly that the greatest impact and difference in results are about the clamped boundary condition. In fact, it should be said that if the CCNT is in the condition of completely fixed both ends, it is very important to know that the CCNT is in the elastic or plastic region. But while the nanotube has more flexible boundaries, the difference in the elastic and plastic stability will be markedly reduced.

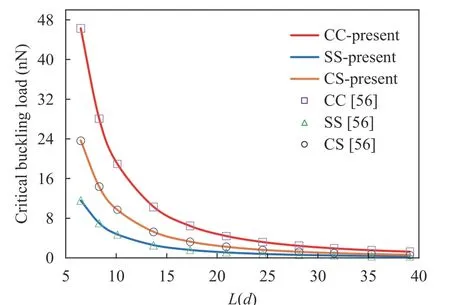
Fig. 3. Comparison of elastic buckling loads for several boundary conditions vs. Ref. [56] for a straight single-walled carbon nanotube(l = 0, e0a = 0, E = 1 TPa, ν = 0.19, d = 1 nm).

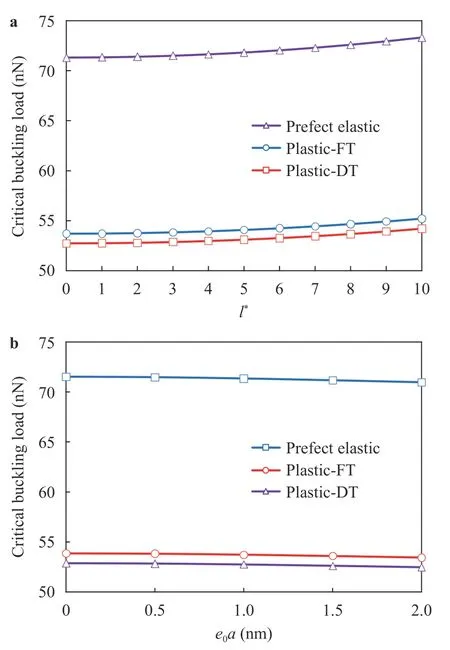
Fig. 4. a Variation effect of the length scale coefficient vs. the three defined (a perfect elastic, flow theory (FT) of plasticity and deformation theory (DT) of plasticity) on the buckling loads for pivot-pivot boundary conditions (L/d = 10, l* = l/h, μ = 1 nm2, e = 0.15L, σ0 = N0,k = 0.25, n = 2). b Variation effect of the nonlocal parameter vs. the three cases (a perfect elastic, FT of plasticity and DT of plasticity) on the buckling loads for pivot-pivot boundary conditions (L/d = 10, l* =1, e = 0.15L, σ0 = N0, k = 0.25, n = 2).

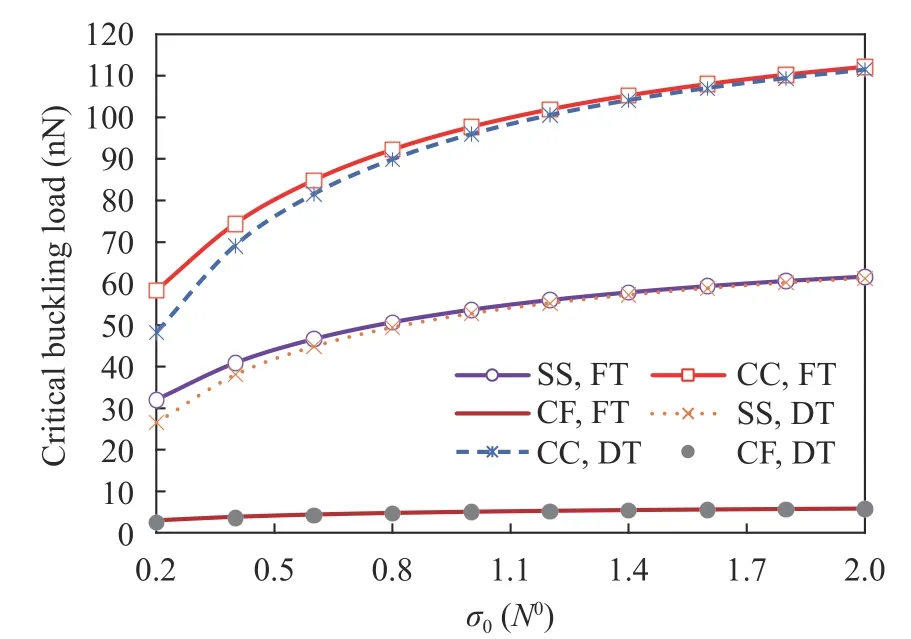
Fig. 5. Variation effect of yield stress vs. different boundary conditions on the plastic buckling loads (L/d = 10, l = h, μ = 1 nm2, e =0.15L, k = 0.25, n = 2)

To study the importance of the value of curvature of the nanotube in the state of the yield of the material, Fig. 6 is produced for each plasticity theory also for different boundary conditions.It is interesting to know if nanotubes are more deformed in the plastic region, its stability will be grown. Of course, the fixed boundary condition is more sensitive to curvature than other ones. On the other hand, it is evident from the figure that, in the large bends of the nanotube, the effects of boundary conditions are gone up and the results of different types of boundary conditions are getting far from one another. It is germane to note that with enlarging the initial deflection, the difference between the results of FT and DT would be further noticeable, in particular for CC edge conditions.

In order to study the parameters n and k in the Ramberg-Osgood relationship, Figure 7(a) and (b) is demonstrated. Both diagrams are provided for the flow theory in the case of clamped edges. In the first figure, it can be seen that with zeroing the value of the parameter n, the variation of the ratio of the yield stress to the current stress does not change the critical loads.This is because in n = 0 the tangent modulus and the elastic modulus are equal in size and the material will be placed in an elastic region, and it presents the problem of the critical elastic load. But as n increases and when the material reaches the full plasticity, results of the critical load for different values of the parameter n get great differences, and as a result, this parameter becomes very important. But in the second diagram, the effect of the variations of both parameters n and k is investigated directly against each other. It is known that when k becomes equal to zero, it gives the full elastic region. As we know of the Ramberg-Osgood relationship, increasing the amount of n to infinite amounts will result in the perfect plasticity, and therefore the critical load and the strength of the material will be greatly reduced. This claim is fully approved by means of Fig. 7(b). Also,the more the parameter k, the weaker the stability of the nanotubes in the plastic region. As a review of Fig. 7(b), it is vividly seen that the increase of the k parameter leads to nonlinear behavior for the curves of results.

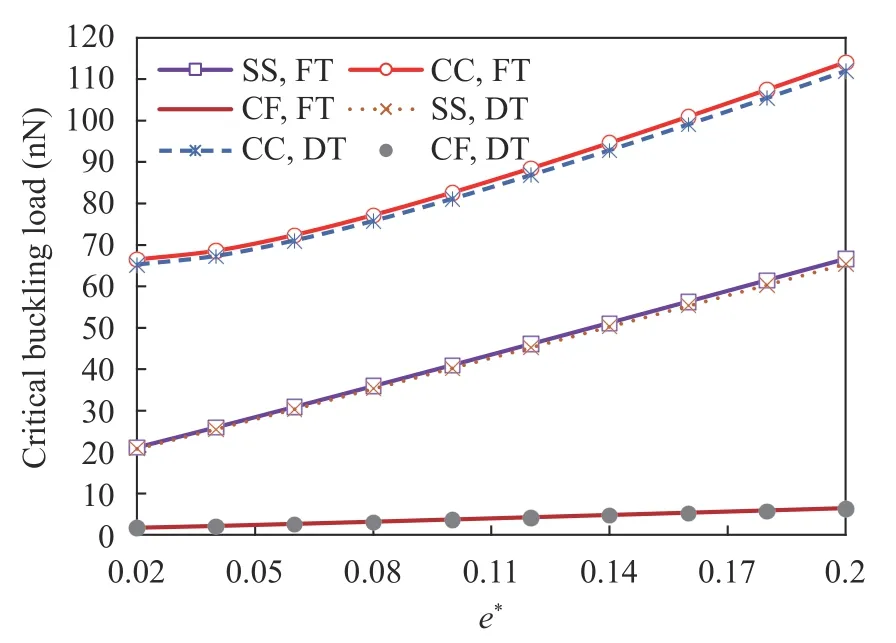
Fig. 6. Variation effect of the curvature parameter vs. different boundary conditions on the plastic buckling loads (L/d = 10, l = h, μ= 1 nm2, e*=e/L, σ0 = N0, k = 0.25, n = 2)

Figure 8 considers the effect of changes in the ratio of yield stress to the current stress of the material against the variations of the nanotube's curvature. In the figure, both the flow theory and deformation approach are studied, while both edges of the nanotube are completely fixed. It is noticeable that in the plastic region the differences in the results of critical loads for various curvatures are less than the differences in the total elastic region.This means that the curvature in a complete elastic state is more important than its amount in the perfect plasticity. Perhaps the concept is that in elastic and reversible situations, the curvature value is important, and in the case where the curvature leads to the plasticity of the material, the importance of the bending rate after the yield of the material is lesser. Of course, only the importance of the degree of curvature after the plasticity of the material is arriving the material at the ultimate stress and then its fracture. It is important to note that in the plastic region, the difference between the results of different curvature when using the flow theory is greater than when using the theory of deformation. In other words, whenever the material is going into full plasticity the difference between the numerical outcomes of both theories of plasticity shows the difference between both hypothesizes.

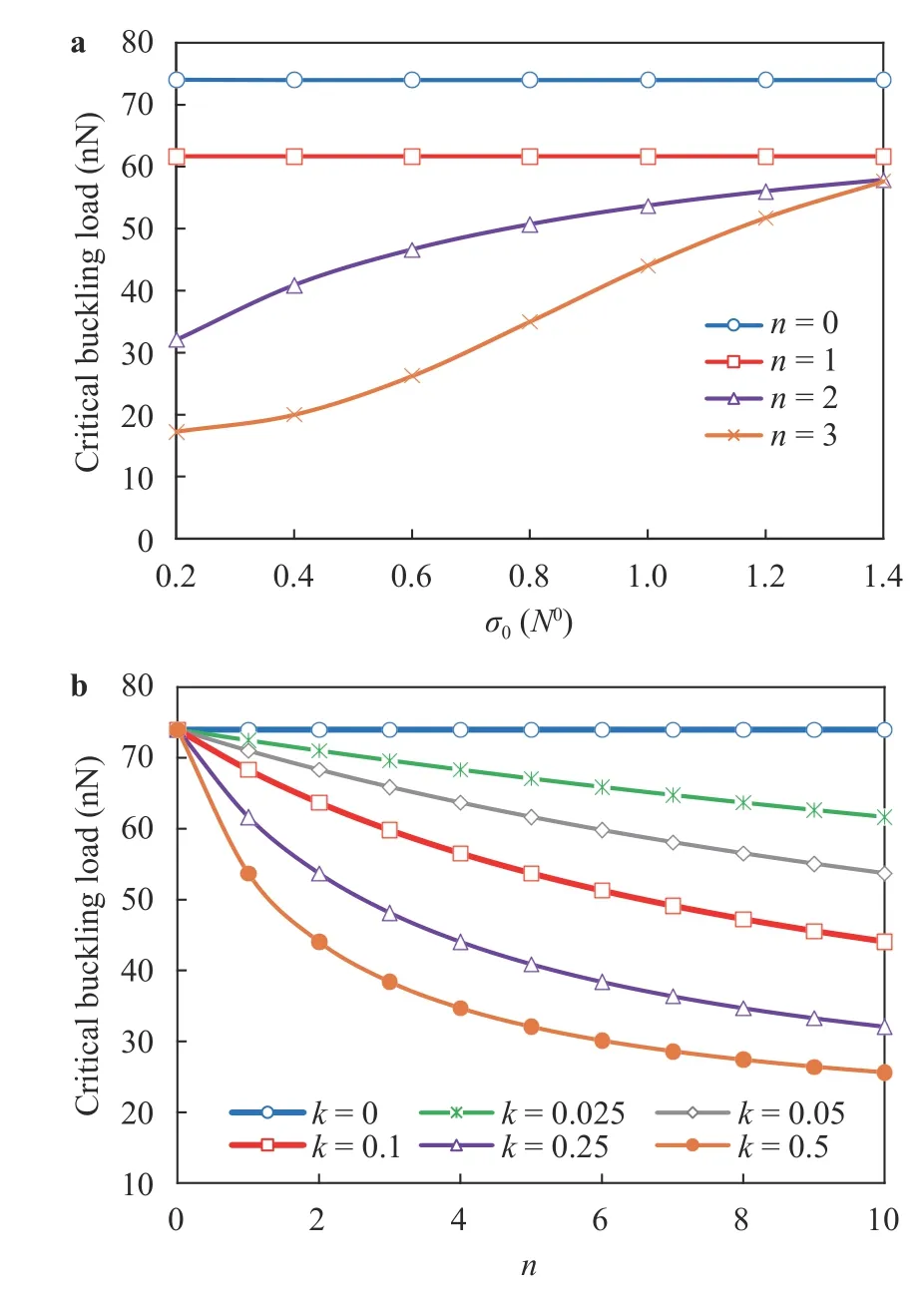
Fig. 7. a Variation effect of the yield stress vs. n parameter on the elastoplastic buckling loads by the flow theory for simply-supported boundary conditions (L/d = 10, l = h, μ = 1 nm2, e = 0.15L, k = 0.25).b Variation effect of the n parameter vs. k parameter on the elastoplastic buckling loads by the flow theory for simply-supported boundary conditions (L/d = 10, l = h, μ = 1 nm2, e = 0.15L, σ0 = N0)

Figure 9 presents the aspect ratio in the flow plasticity theory for a variety of boundary conditions. The figure is provided to be examined in the yield point. That is, the material is neither perfectly elastic nor completely plastic. It is observed that the longer the nanotube's length, the lower the stability. Also, whatever the nanotube's length growths, the results of the different boundary conditions are closer to each other. So that we obtain the important result that the boundary condition becomes less important in the nanotubes with very long lengths. On the other side,the effect of changing the length of the nanotube for the fixed boundary condition is much greater than the other boundary conditions. This is due to the steep slope of the results of the fixed boundary condition with the increase of the aspect ratio(L/d).

This paper discussed the elastoplastic stability of CCNT in a nanoscale domain concerning both plasticity theories, namely,flow and deformation plasticity concepts. Accordingly, to demonstrate CCNT in nanoscale, the model of nonlocal strain gradient theory was captured. The semi-analytical procedure regarding the Rayleigh-Ritz solution technique was adopted for which a new admissible function was also derived. The study performed on the plotted outcomes and several considerations were shown on the determination of elastoplastic and plastic buckling loads of CCNTs. The highlighted results are briefed as below.

Fig. 8. Variation effect of the yield stress vs. different curvature on the elastoplastic buckling loads for clamped-clamped boundary conditions (L/d = 10, l = h, μ = 1 nm2, k = 0.25, n = 2)

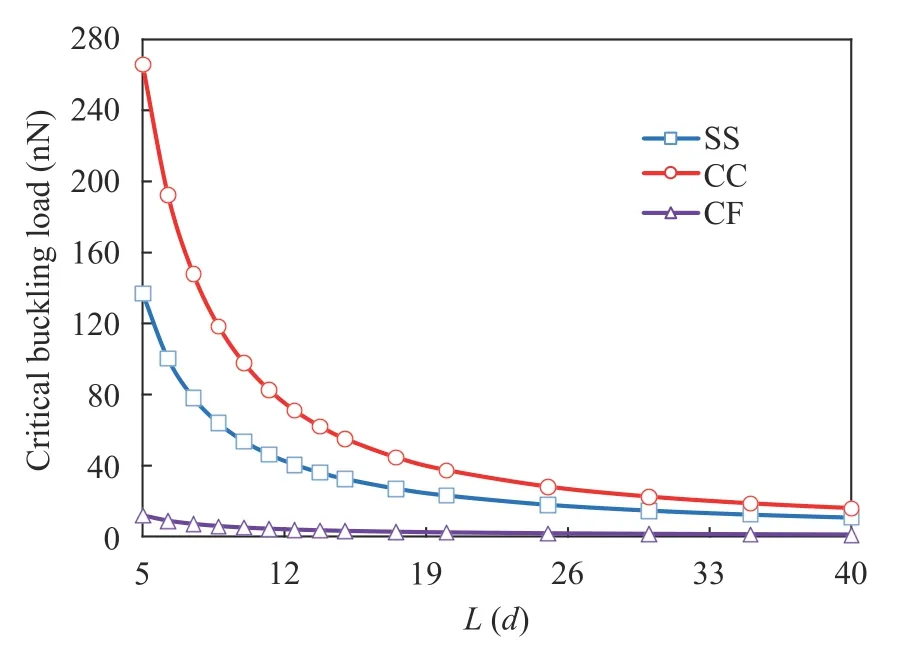
Fig. 9. Variation effect of the aspect ratio (L/d) vs. different boundary conditions on the plastic buckling loads by the flow theory (l = h,μ = 1 nm2, e = 0.15L, σ0 = N0, k = 0.25, n = 2)

· It was importantly shown that as the plastic stability of CNTs is less than elastic one, the structure should also be taken in a plastic analysis. Because the structure can be failed by stresses lower than elasticity modulus in a plastic region and an elastoplastic or even plastic behavior may be unpredictable in light of the working environment of the material.

· The CCNT has further resistance in an elastic region against a plastic one.

· The variation of nonlocal and strain gradient parameters lead to softening and hardening into both elasticity and plasticity regions.

· The elastoplastic and plastic buckling loads for FT are greater than DT.

· The increase of curvature leads to increasing the values of critical buckling loads in the elastoplastic region. And for a large curvature, the effect of boundary conditions increased fundamentally.

· The effect of boundary conditions for FT is more than DT.

· Increasing the yield stress of the CCNT makes the results of FT and DT in various boundary conditions as same as each other.

· When the value of yield stress is more than the maximum stress, the curvature is more significant. In other words, the value of curvature in an elastic region (recoverable curvature) is more important than a plastic one.