Prolonged simulation of near-free surface underwater explosion based on Eulerian finite element method
2020-03-27MingHeManZhangYunLongLiu
Ming He, A-Man Zhang*, Yun-Long Liu
College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
Keywords:Bubble dynamics Underwater explosion Free surface Eulerian finite element method
ABSTRACT In the area of naval architecture and ocean engineering, the research about the underwater explosion problem is of great significance. To achieve prolonged simulation of near-free surface underwater explosion, the underwater explosion transient numerical model is established in this paper based on compressible Eulerian finite element method (EFEM). Compared with Geers-Hunter formula, EFEM is availably validated by simulating the free-field underwater explosion case. Then, the bubble pulsation and flow field dynamic characteristics of the cases with different underwater explosive depth are compared in this work. Lastly, the height of the water hump and the pressure of flow flied are analyzed quantitatively through the simulation results.
Bubble dynamics is a critically vital research topic in a great deal of fields [1-4], especially in underwater explosion field [5-7].In modern naval battles, the underwater explosion of weapons in the water such as torpedoes and mines is one of the important reasons for the damage of ships [8]. The shock wave generated by the explosion causes transient damage to the structures,and then the pulsating bubble will continuously affect the vitality of the ships for a long time. At the same time, the water hump produced by the near-free surface explosion will also alter the movement characteristics of the ships [9]. Therefore, studying and mastering the physical mechanism of the full-cycle underwater explosion process is of great engineering significance.
As early as the last century, Rayleigh, Plesset and other scientists established the Rayleigh-Plesset equation to describe the bubble dynamics problem [10]. For the whole process of real and complex underwater explosion problem, accurate analytical solutions are difficult to obtain. Experimental research is one of the reliable tools for researching underwater explosion problem.The countries with strong military strength such as the United States conducted underwater explosion tests on several occasions. In addition, some scientists used the scale model experiments to explore the mechanism of this problem [5, 11-13].However, factors such as experimental cost and period limit its wide range of engineering application. In contrast, numerical simulation has extremely significant advantages [6, 14-17]. Numerical simulation can save costs and simulate a large number of different cases in real time. At present, there are many works to study the underwater explosion problem by numerical simulation.
Aiming at the current research status and the important research significance of underwater explosion problem, the underwater explosion transient numerical model is established in this work on account of compressible EFEM. The near-free surface underwater explosion problem is mainly studied in detail. The schematic diagram of near-free surface underwater explosion is shown in Fig. 1. Firstly, the numerical model is validated by simulating the free-field underwater explosion case. Then, the bubble pulsation and flow field dynamic characteristics of the cases with different underwater explosive depth are compared.Lastly, the height of the water hump and the pressure of fluid flied are analyzed quantitatively through the simulation results.
The compressible EFEM has obvious advantages in disposing of transient large deformation problems [18-21]. For the sake of studying the mechanization of underwater explosion problem, the physical model is simplified into an axisymmetric model, which is relative mature for grid methods. This treatment improves the solution efficiency of the problem while ensuring the accuracy of the result. The governing equation of each element in this model is as follows
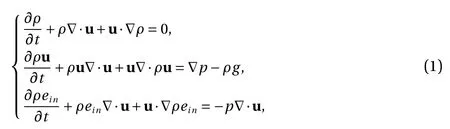
where einisthe specific internalenergyper unit mass, ρisthe densityofthematerial, u={ur,uz}isspeed vector and gisthe gravitationalacceleration. Wemust payattention tothatwhere the subscript, i indicates the partial derivative with respect to the coordinate in the orientationi. The above equation is established in cylindrical coordinate system,where z and r are the axial and radial coordinates respectively.Equation (1) is separately the mass, momentum and energy equations, which can be written in a uniform format to solve the governing equations systematically, namely,

where φ is unknown variable, and S is source item. Based on operator separation method, Eq. (2) can be divided into Eulerian and Lagrangian steps, which is the core idea of EFEM. The schematic diagram of EFEM is shown in Fig. 2.
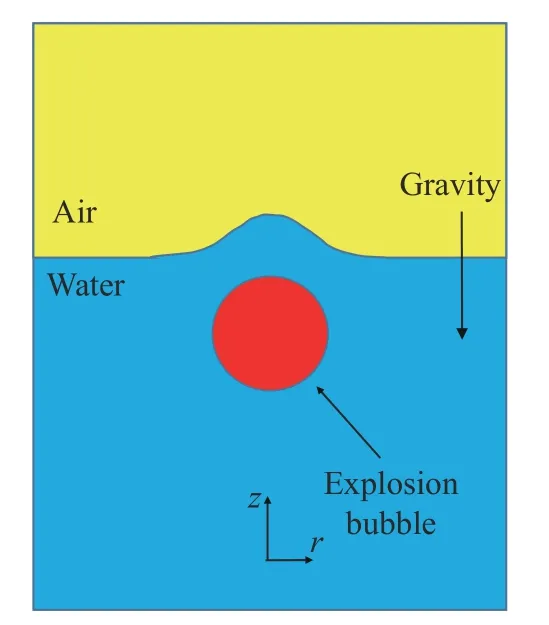
Fig. 1. Schematic diagram of near-free surface underwater explosion.
Adopting the explicit finite element method, Eq. (2) is solved in the Lagrangian step firstly where the source item is ignored.The Galerkin formula used for solving the momentum conservation in cylindrical coordinate system could be derived from the Gauss-Green formula and the integration by part, namely,
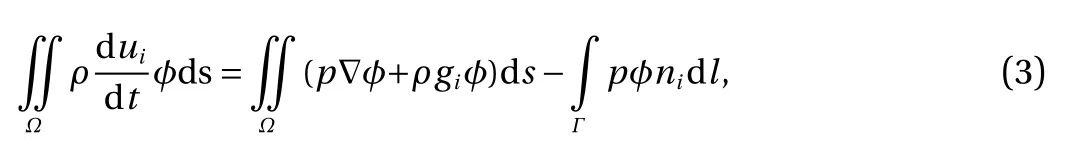
where Ω is the dispersed two-dimensional orthogonal computationregion, niistheunitarynormalvectordirectingthe outside of region in theithorientation,Γistheboundaryofthe Ω , and φ is the computational shape function. Equation (3) can besolvedbydispersing.Afterwardsthevelocity uiand displacementxoffluid nodeare renewedwiththe high-order explicit integral format and the mesh advances with the fluid parameter, namely,

where δt is the time increment, a is the acceleration obtained by Eq. (3) and the superscript denotes the increment count. Then,thenewfluiddensityandthe specific internalenergyeinare renewedwiththe massandenergy conservingequation,namely,

At this time, the Eulerian step begins which is demanded to move back the deformed mesh to its initial position after the Lagrangian step. It is worth mentioning that the volume of fluid method (VOF) is used to capture the fluid interface in Eulerian step and the monotonic upwind scheme for conservation laws can improve calculation accuracy [9]. After the Eulerian step, the pressure p is renewed with the material equation of state for the next increment. So far, the operation of a time step is over.
The equation of state is important for numerical model which is related to the pressure, internal energy and density together. In this model, the equation of state of the water and air is chosen as the Tammann equation [22], namely,
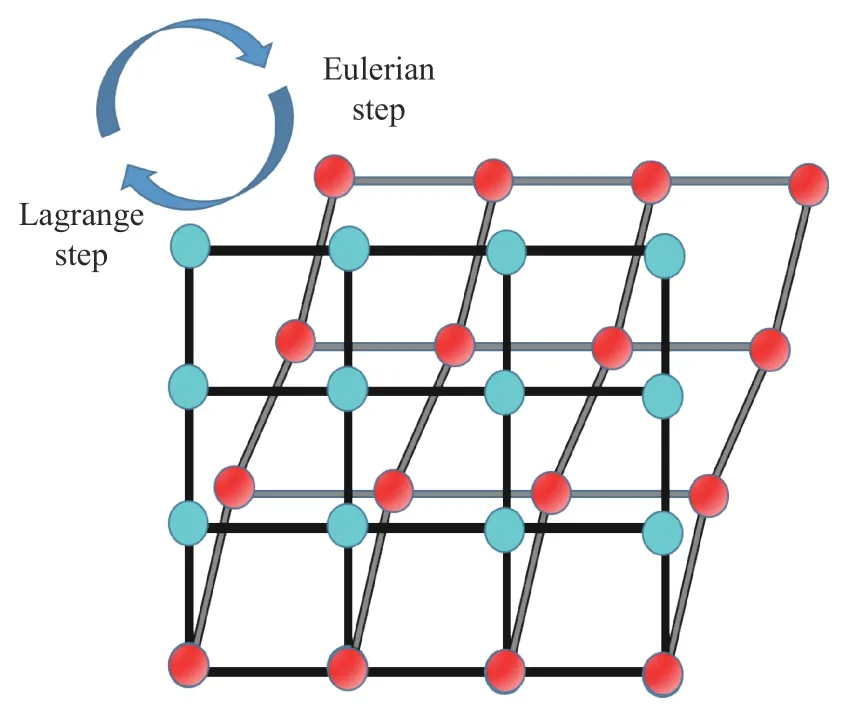
Fig. 2. Schematic diagram of EFEM.

where Pwis the reference, γ is the specific value of heat. The equation of state of the explosive products are solved by Jones-Wilkens-Lee (JWL) equation [22], namely,
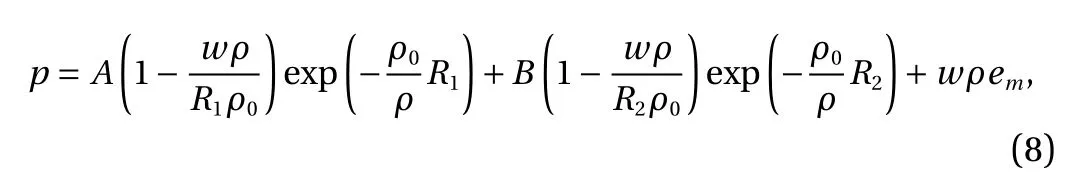
where A,B, R1, R2and w are the specific constants for material,ρ0and ρ are respectively the densities of the explosive and the explosive products. And the fluid constants for equation of state is shown in Table 1.
For free-field underwater explosion condition, the current model is relatively reliable. In this work, the correctness of the numerical model is availably validated by comparison with the Geers-Hunter model [23, 24]. Based on the underwater explosion problem studied in this paper, the large equivalent (110 kg)explosive underwater 100 m explosion case is simulated. Among them, the calculation domain is 50 m×50 m, the number of grids is 160000, the pressure measuring point is located 25 m away from the initial explosive position and the calculation boundary is a non-reflection boundary [25]. The bubble equivalent radius R and bubble migration distance Z curves of the two models areshown in Fig. 3. And the pressure comparison curve of the two models is shown in Fig. 4.

Table 1 Specific material constants for equation of state [22].
It can be drawn a conclusion from the Fig. 3 that the numerical model of the free-field explosion established in this paper agrees well with the Geers-Hunter model. In the bubble expansion stage, the bubble equivalent radius and the bubble migration distance curve are substantially identical. Since the Grees-Hunter model is based on the spherical bubble system and the no-spherical motion is considered in EFEM model under buoyancy, there are differences between the two models at the stage of bubble collapsing and jet generation. When the underwater explosion bubble reaches a certain volume, the bubble movement especially the pulsation cycle will change due to buoyancy.In addition, the pressure change trend and the second pulsation pressure peak of the two models are consistent as shown in Fig. 4. And the numerical viscosity reduces the peak value of the shock wave in numerical simulation. In summary, the numerical model established in this work has enough calculation accuracy.
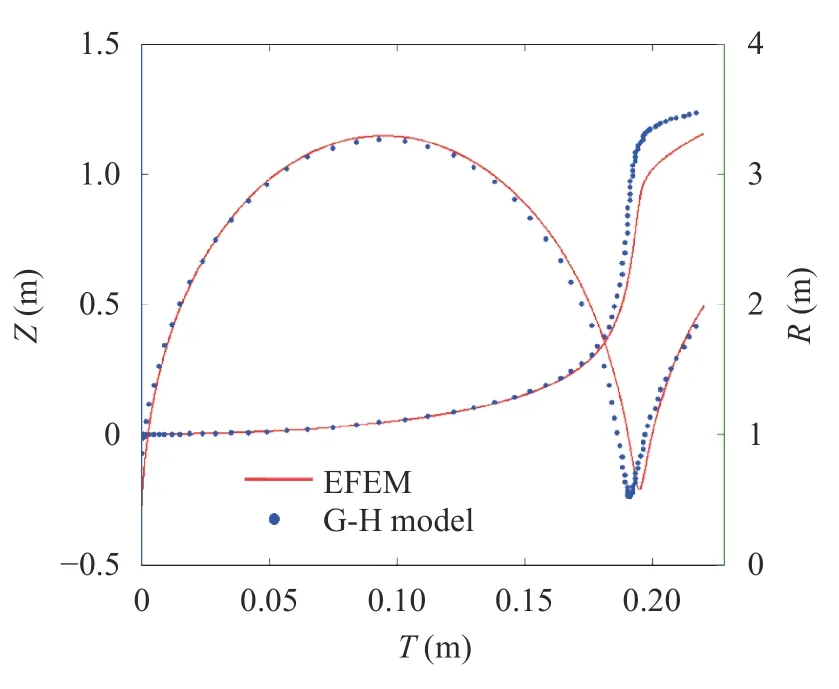
Fig. 3. Bubble equivalent radius and bubble migration distance curves of the two models (G-H model means Geers-Hunter model)
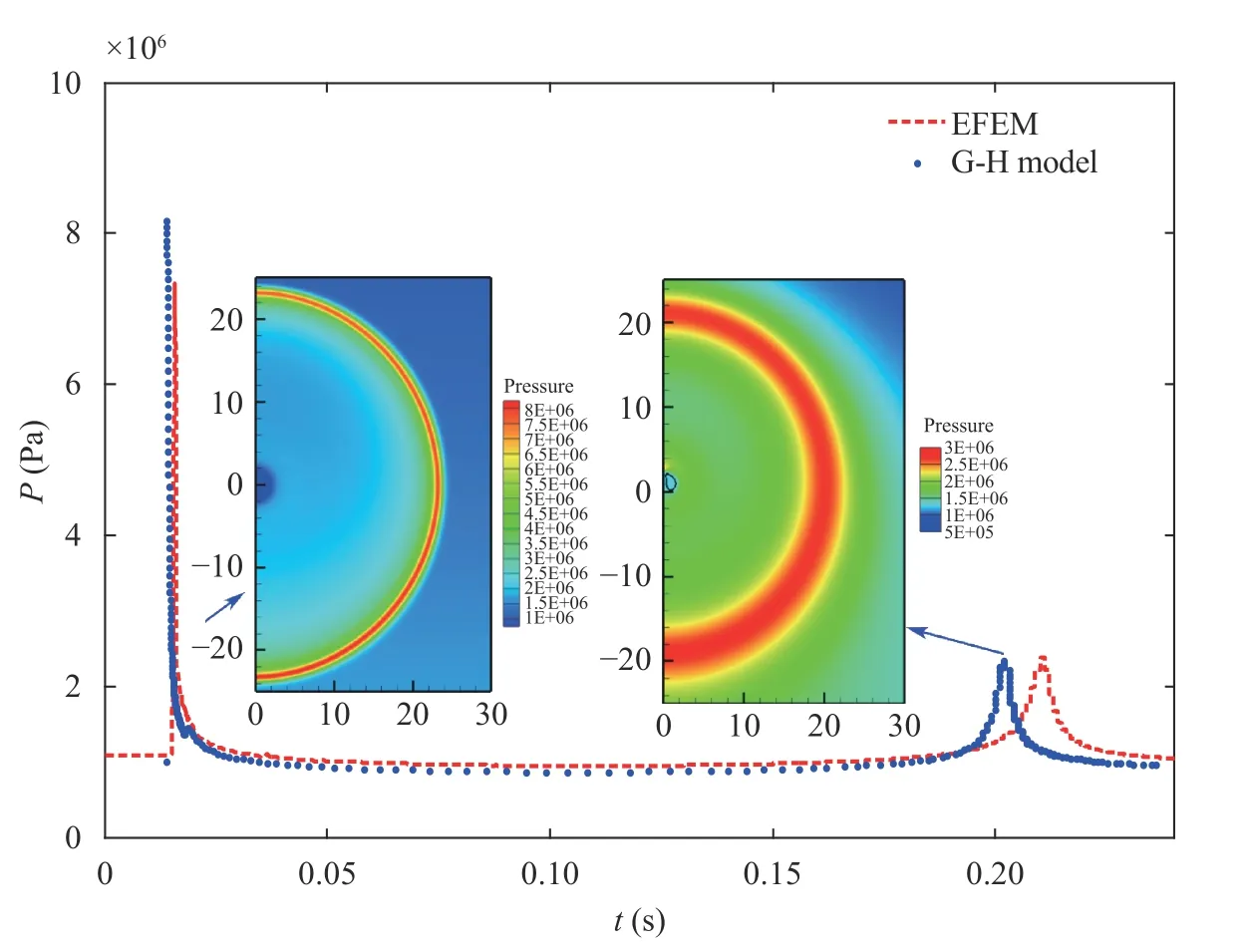
Fig. 4. Pressure comparison curve of the Geers-Hunter model and EFEM.
In this work, the underwater explosion of which the explosive depth is less than twice the maximum diameter of the bubble is defined as the near-free surface underwater explosion. In order to study the mechanization of underwater explosion problem, this work selects three cases (650 kg explosive under the conditions of 5 m, 10 m, and 20 m explosive depth) for comparative analysis. And the three cases are named case 1, case 2 and case 3. Among them, the calculation domain is 50 m×200 m, the grid size is 0.5 m, the calculation boundary is also a non-reflection boundary, and the pressure measuring point is located 40 m away from the initial explosive position and 50 m away from the free surface. Figures 5 and 6 show the changes of free surface and flow field pressure for case 1 and case 3. In addition, d represents the distance between the detonation and the free surface in the following paper.
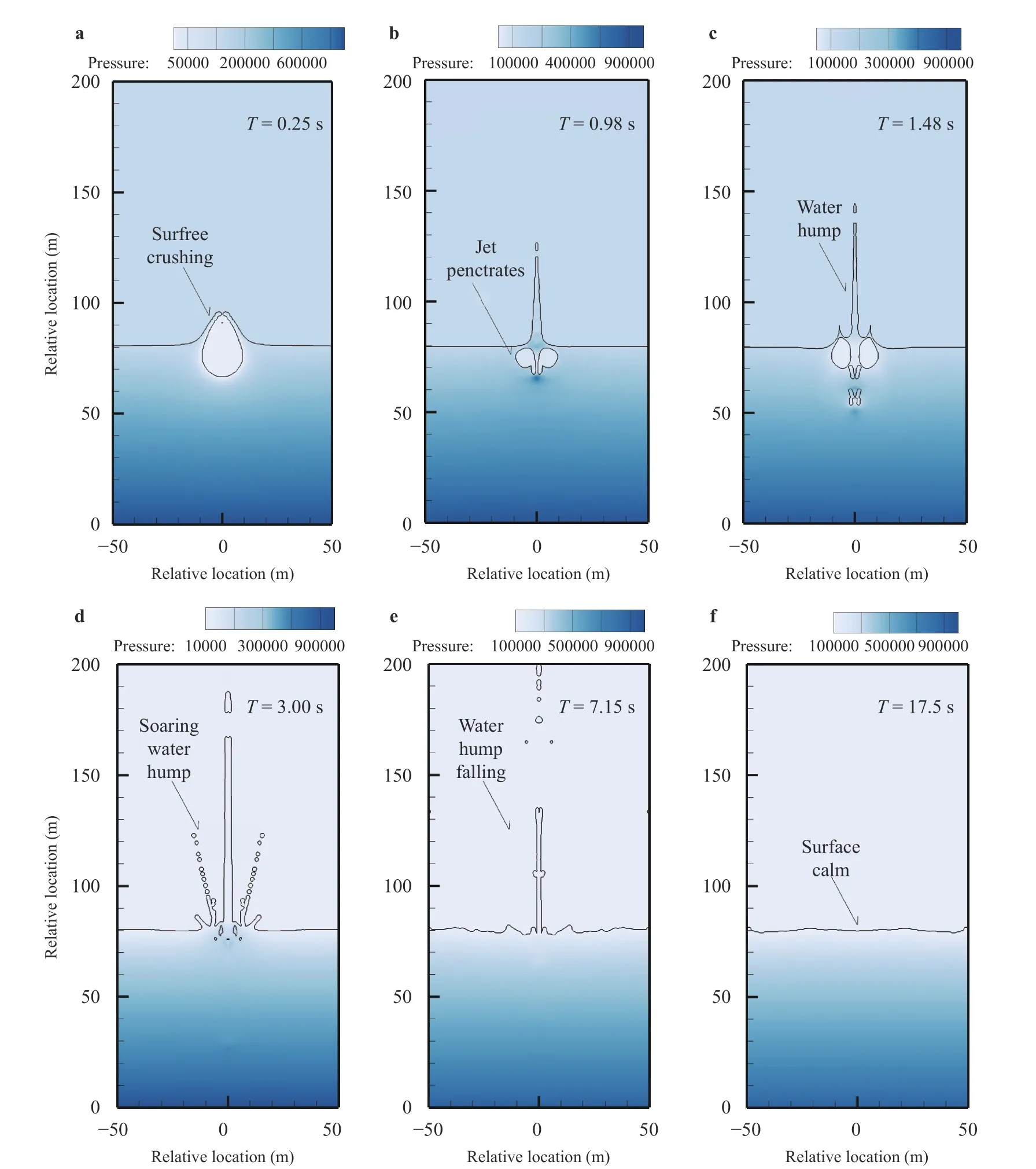
Fig. 5. Changes of free surface and flow field pressure for case 1 (650 kg explosive under the condition of 5 m explosive depth), surface crushing is shown in a, jet penetrates is shown in b, soaring water hump is shown in c and d, water hump falling is shown in e and surface calm is shown in f. Black line indicates interface outline.
There are significant differences in flow field characteristics for underwater explosion with different explosive depth. It can be seen from Fig. 5 that when the distance d is smaller than the maximum radius of the bubble, the free surface breaking and reclosing will emerge in the bubble expansion stage. Moreover, the subsequent bubble pulsation at the free surface causes sharp splash of the free surface. The water hump is simulated vividly and its evolution is divided into three stages including production, soaring and falling. At the same time, the height of the water hump at the free surface can reach the order of 100 m as shown in Fig. 7, which is called the soaring water hump. The reason for the phenomenon is that a large amount of energy generated by the bubble can be transmitted to the free surface under this case, which causes vigorous movement of the fluid. At the moment of the explosion, the free surface fluid gained a larger speed and soared upward. What's more, the fluid can reach a higher height under the induction of inertial force. We must mention that this case is difficult to simulate by traditional numerical methods.
As shown in Fig. 6, when the distance d is bigger, the bubble will firstly expand in form of spherical bubble and then rise under the effect of buoyancy. When the bubble rise to the free surface, it will also induce the production of water hump. At this time, the height of the water hump is lower, which is called mound water hump in this work. Compared with the case in Fig. 5, the free surface movement of this case is relatively stable.In addition, as the energy continues to dissipate, the free surface tends to calm after the underwater explosion for the two cases as shown in Figs. 5(f) and 6(f), which means the end of the underwater explosion. In a word, it can be seen from Figs. 5 and 6 that this paper can vividly and effectively simulate the full-cycle nearfree surface underwater explosion problem. And these two cases are typical and of great significance.
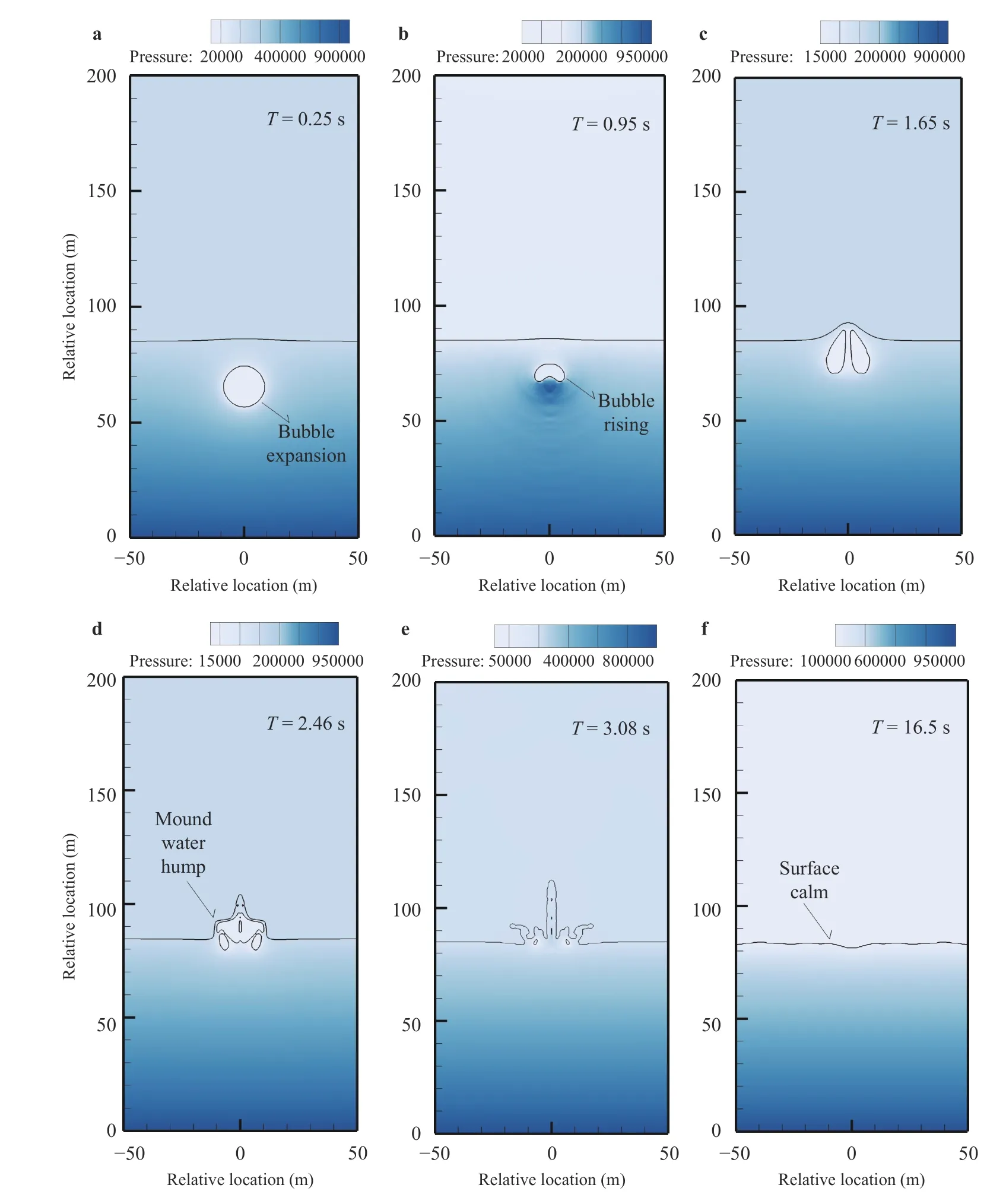
Fig. 6. Changes of free surface and flow field pressure for case 3 (650 kg explosive under the condition of 20 m explosive depth), bubble expansion is shown in a, bubble rising is shown in b, mound water hump is shown in d and surface calm is shown in f. Black line indicates interface outline.
The water hump is an iconic phenomenon for near-free surface underwater explosion. The water plume height is considered to be the distance between the highest water element and the free surface in this paper. As shown in Fig. 7, there are obvious differences in the change trend of water hump height for different explosive depth. When d=5 m, the water hump climbs directly up to 100 m. At this time, the free surface obtains more energy produced by bubble movement. When d equals 10 m and 20 m respectively, the height of water hump is lower at the stage of bubble expansion and reaches its peak value at the stage of bubble pulsation. We can also make a conclusion that when the explosive position reaches a certain depth, the peak of water hump is similar which is resolved by the total energy of system.For different explosive depth cases, there is the phenomenon of water hump pulsation in the later stage. This is caused by the unstable flow and involving the mutual transformation of kinetic energy and potential energy. When t=15 s, the free surface almost restores calm. In other word, the full cycle of the 650 kg TNT underwater explosion process is about 15 s from numerical simulation result. Due to the complexity of the real sea conditions, the cycle in reality may be longer.
Pressure load is an important parameter for underwater explosion problem. It can be seen from the Fig. 8 that when d=20 m, the moment for the bubble to generate the jet is obviously advanced. Since when the explosion bubble is far away from the free surface, the buoyancy effect will be obvious. Under the action of buoyancy, the bubble will generate an upward jet. When d=5 m, the bubble generates a smaller secondary pulsation load due to the free surface breaking in the bubble expansion stage and part of the energy generated by the bubble is directly diffused into the air. When d=10 m, the secondary pulsation load generated by the bubble is the largest, so the damage effect of the underwater explosion is not linearly related with the distance d. The peak value of the bubble pulsation load is related to the minimum volume of the bubble. The more obvious the nonspherical motion, the greater the kinetic energy of the external flow field at the minimum volume, the smaller the internal energy of the bubble, and the smaller the pulsating pressure of the radiation. The free surface induce bubble to create a downward jet and the buoyancy induce bubble to create an upward jet.When d =10 m the bubble shape is closer to the sphere due to the offset effect of free surface and buoyancy, the pulsating pressure is bigger. In addition, through the local pulsation phenomenon of the pressure change curve, the reflection effect of the free surface on the shock wave can be seen.
The underwater explosion transient numerical model is established in this paper on account of compressible Eulerian finite element method to achieve the prolonged simulation of near-free surface underwater explosion. Compared with the existing model, the results fully verify the correctness of the numerical model. Then, the analysis of three cases with different explosive depth are carried out. This paper concludes that when the distance d is smaller, free surface breaking and reclosing will emerge in the bubble expansion stage, and the movement of the surrounding flow field is very intense. When the distance d is bigger, the bubble will expand firstly and then collapse, and the movement of the surrounding flow field is relatively stable. It can be seen from the pressure change curve that the damage effect of the underwater explosion is not linearly related with the distance d. The free surface induce bubble to create a downward jet and the buoyancy induce bubble to create an upward jet. When the bubble is closer to the spherical motion because of the offset of free surface and buoyancy, the pulsating pressure is bigger.
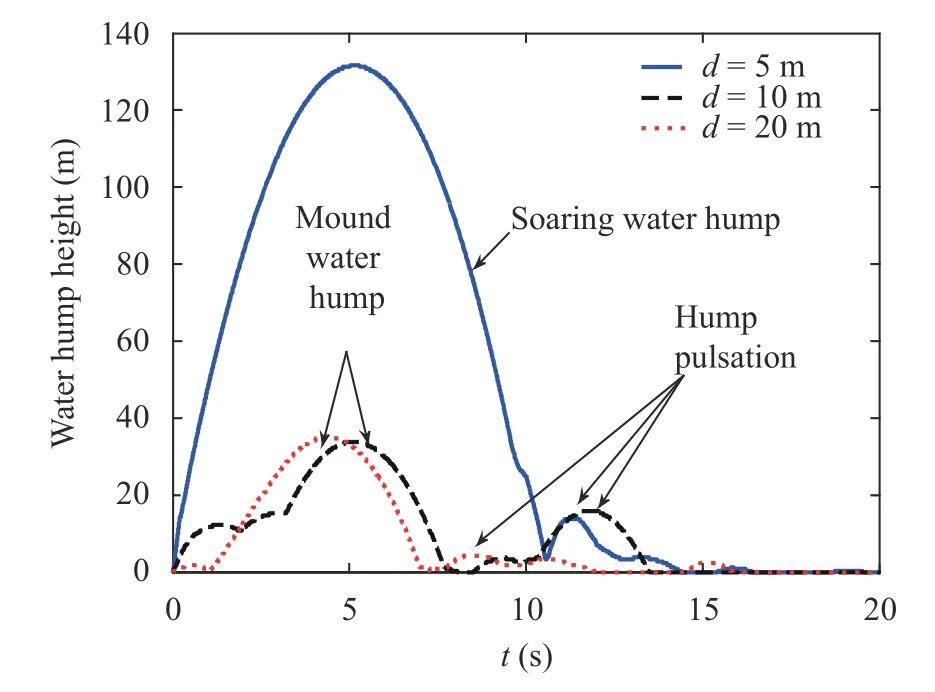
Fig. 7. Water hump height change curves for different explosive depth cases.
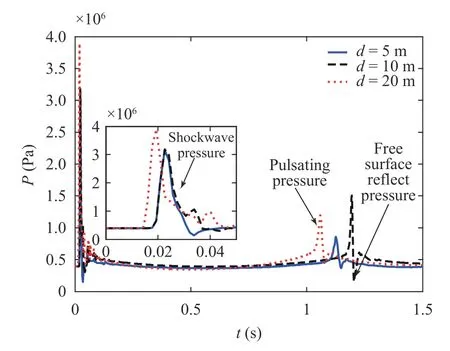
Fig. 8. Comparison of pressure change curves for different explosive depth cases.
Acknowledgements
The authors would like to acknowledge the support of the National Natural Science Foundation of China (Grant 11672081)and the Industrial Technology Development Program (Grants JCKY2018604C010 and JCKY2017604C002). Finally, Thanks for the help of Zu-Hui Li during writing the paper.
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Micromechanical analysis on tensile properties prediction of discontinuous randomized zalacca fibre/high-density polyethylene composites under critical fibre length
- Neurodynamics analysis of cochlear hair cell activity
- Minimizing electrostatic interactions from piezoresponse force microscopy via capacitive excitation
- Spatial artificial neural network model for subgrid-scale stress and heat flux of compressible turbulence
- An analytical model to predict diffusion induced intermetallic compounds growth in Cu-Sn-Cu sandwich structures
- Molecular investigation on the compatibility of epoxy resin with liquid oxygen
