基于FPGA实现快速矩阵求逆算法*

张 繁，何明亮

（上海诺基亚贝尔股份有限公司，江苏 南京 210037）

0 引 言

矩阵求逆在接收抗干扰信号处理中应用广泛。相比传统的矩阵求逆算法，基于cholesky分解的矩阵求逆算法，大大简化了求逆运算量。在接收抗干扰处理和权值更新的过程中，用时越长，则定位误差越大。用FPGA的流水线设计来实现cholesky分解求逆算法，则能充分体现出“实时”特性，对抗干扰处理有十分重要的意义。矩阵求逆算法RTL编码在FPGA设计中开发难度大、效率低，这里研究了一种基于自相关矩阵的cholesky分解求逆算法在FPGA中的实现。

1 Cholesky分解方法

Cholesky分解矩阵[1]方法是利用协方差矩阵A厄米特（Hermitian）正定的特性，将协方差矩阵A分解为上/下三角矩阵L及其共轭矩阵的乘积。计算出上/下三角矩阵的逆矩阵P，通过求取上/下三角矩阵的逆矩阵的共轭矩阵PH及矩阵P的乘积，即可得到原协方差矩阵A的逆矩阵。下面以分解为下三角矩阵为例介绍Cholesky分解[2-3]求逆算法。

1.1 Cholesky分解

Am是对称正定矩阵，是矩阵的Choleksy分解，其中Lm是一个具有正的对角线元素的下三角矩阵，即：

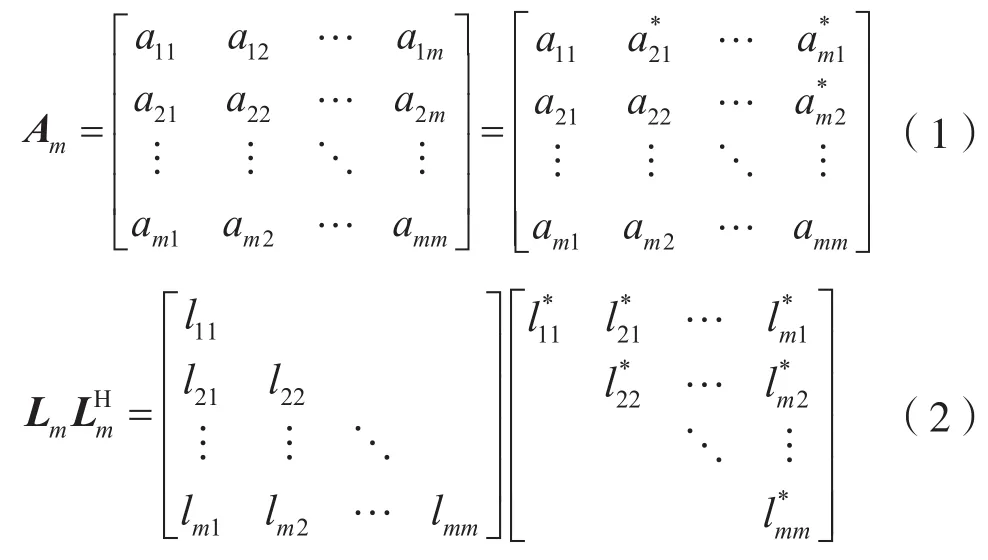
采用分块法计算Lm矩阵。令Lm由分块矩阵L11、0、L1和Lm-1构成。其中，L11为1×1的标量；0为1×(m-1)的行向量；L1为(m-1)×1的列向量；Lm-1为 (m-1)×(m-1)的矩阵。

同理，将Am由分块矩阵a11、a1和Am-1构成。

可以得出，Lm第一列的值可由Am的第一列的值算出，即：

由此产生的新矩阵为：

按照上述相同的矩阵分块的方法，即可计算出Lm-1第1列的值，即Lm第二列的值；以此类推，即可计算出下三角矩阵Lm的值。

1.2 下三角矩阵求逆

Am的求逆运算公式为：

Lm的值已经求出，下面就是对Lm求逆。

设Pm为Lm的逆矩阵，即，则有：

分析式（9）可以得出Pm也为下三角矩阵，而Pm主对角线的值分别为：

次对角线计算方法如下。

由：

可得：

依次类推，可以计算出Pm矩阵第三对角线以及所有其他元素的值。

1.3 矩阵相乘

根据计算的下三角矩阵Pm，实现Pm与Pm共轭矩阵的相乘，最终得到矩阵Am的逆矩阵：

2 FPGA实现

以m=9为例，基于FPGA实现9×9复数矩阵的求逆运算。图1为基于矩阵求逆的抗干扰模块实现框图。

其中，关于9×9复数矩阵A的求逆运算模块如图2所示。

图1 基于矩阵求逆的抗干扰实现模块

图2 9×9复数矩阵求逆模块

对9×9复数矩阵A进行Cholesky分解过程的模块框图如图3所示。

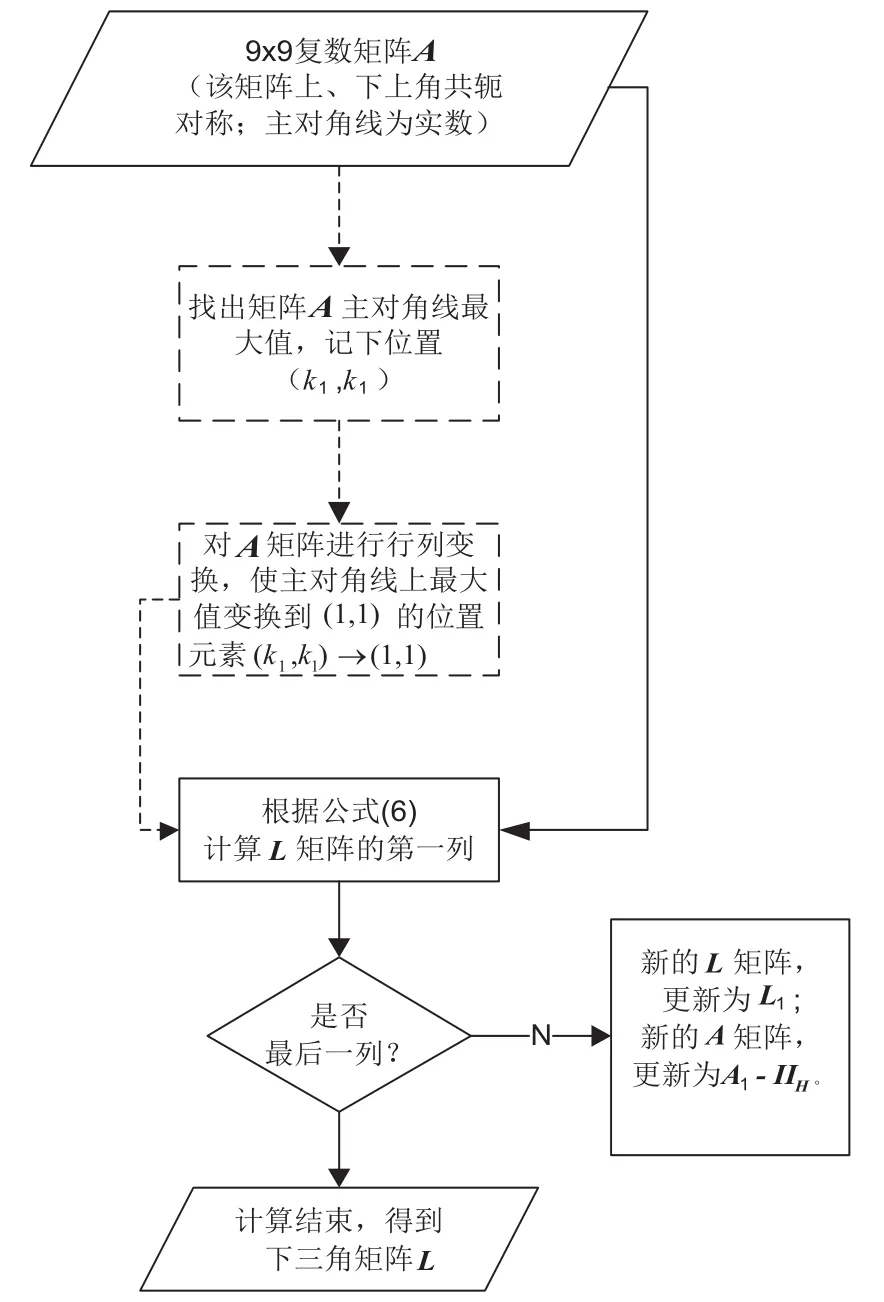
图3 9×9矩阵Cholesky分解模块

图4为9×9矩阵Cholesky分解模块框图，该模块完成9×9下三角复数矩阵L的求逆[4]运算，矩阵L的主对角线为实数。公式L*P=E中，L的逆矩阵P也是9×9下三角矩阵，P的主对角线为L的主对角线的倒数。下三角矩阵求逆模块，如图5所示。

图4 循环展开框

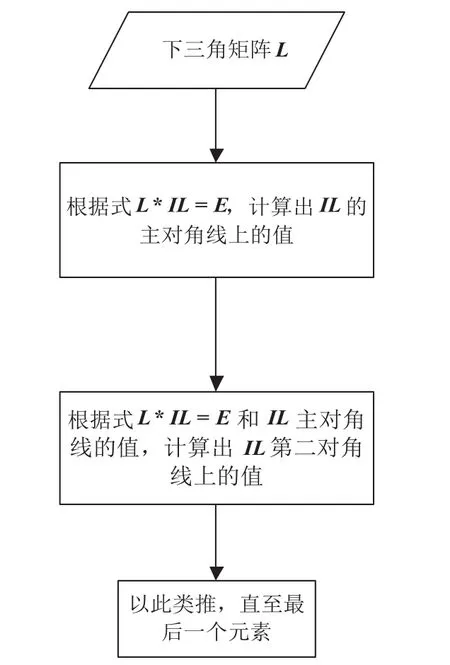
图5 下三角矩阵求逆模块

3 Matlab效果验证

表1为四阵元、三干扰以及干扰强度为-65 dBm的环境下Matlab的仿真结果。

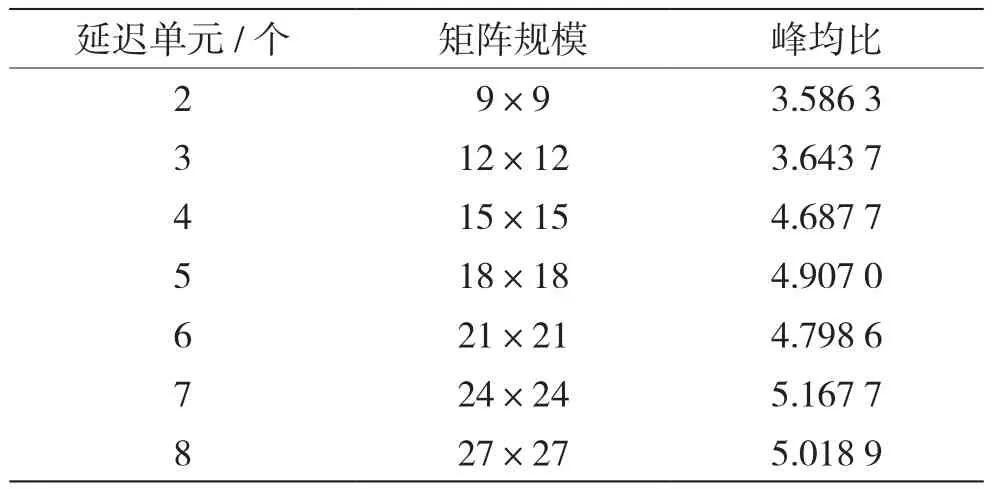
表1 Matlab仿真结果对比

在该种环境下选取24×24矩阵为最优结构。图6为24×24矩阵结构下Matlab的运算结果。

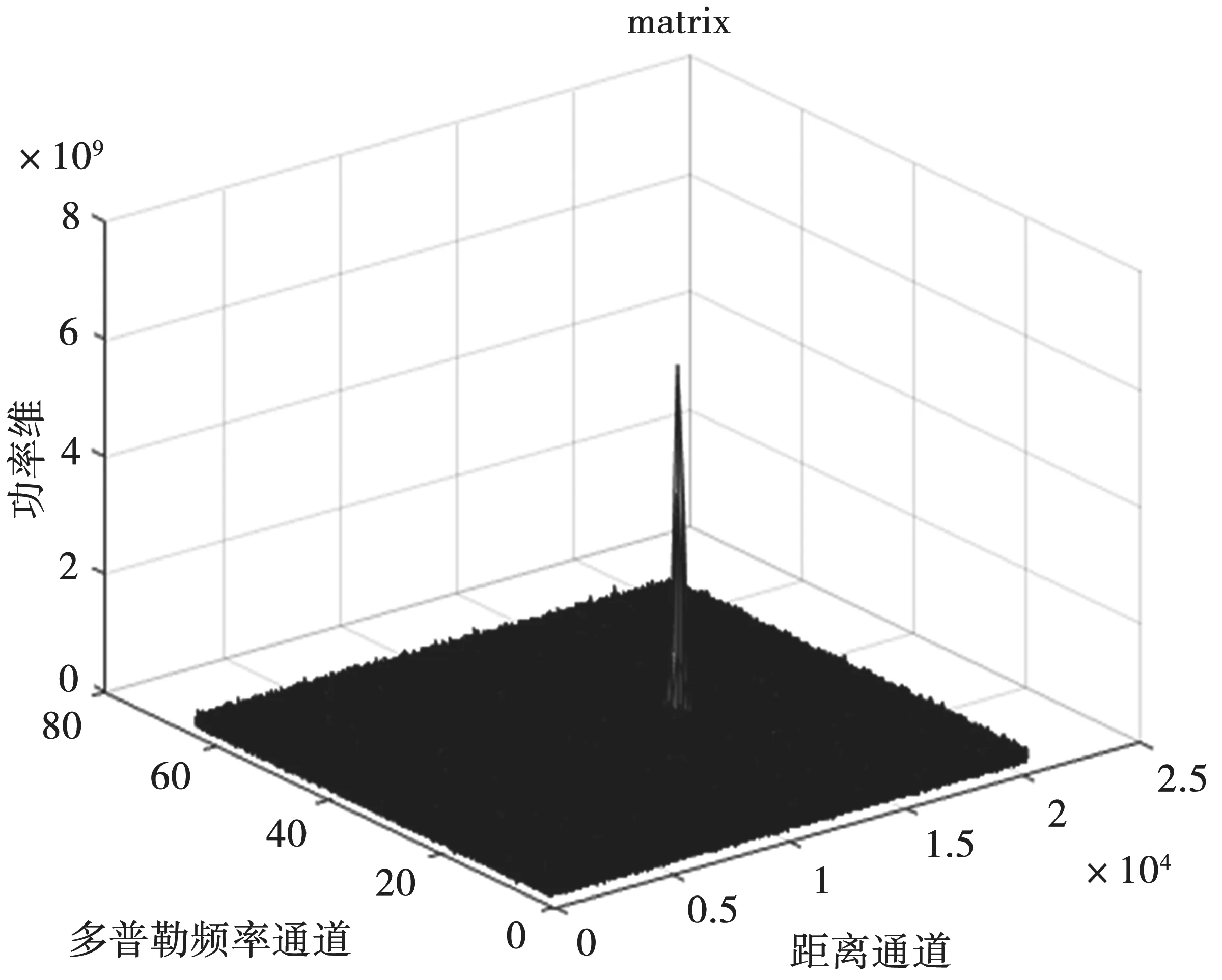
图6 Matlab仿真结果

4 结 语

基于Cholesky分解的矩阵求逆算法，利用FPGA流水线设计特点在FPGA中实现该算法，其实时性在接收抗干扰应用中有着十分重要的意义。结合实际环境、需求以及FPGA设计资源等因素，可以合理选取最优结构进行抗干扰处理。